40.Числовые характеристики случайных величин.

Закон распределения плотностью описывает СВ. При решении некоторых задач не нужно знать полное описание СВ. Достаточно знать только отдельные ее числовые характеристики.

Важнейшие характеристики СВ

• Математическое ожидание СВ (МО)

• Дисперсия СВ

• Среднее квадратическое отклонение СВ

МО (среднее значение) ДСВ называется сумма произведений всех ее возможных значений на соответствующие вероятности.

M(X)=

МО НСВ Х с плотностью распределения вероятностей f(x) называется число находимое по формуле. M(Х)=

1. М(С)=С, С=const

2. М(С*x)=C*М(С)

3. М(x_+y)= М(x)_+ М(y)

M(x)=a

Дисперсией (рассеивание значений вокруг CB вокруг среднего значения) СВ х называется МО квадрата отклонения случайной величины от ее мат.ожидания.

D(x)=M(x-a)² (1)

Используя свойства МО ф-ла (1), можно преобразовать к виду более удобному для вычислений

D(x)=M(x)^{2 _} (a)²

Запишем ф-лы (1) и (2) для дискретной CB x:

1. D(x)= ∑ (x_i-a)²*p_i (1ⁱ)

D(x)= ∑x_i²*p_i - a² (2ⁱ)

2. для непрерывной CB x:

D(x)= ∫ (x-a)²*d(x)dx (1ⁱⁱ)

D(x)= ∫ x²*f(x)dx-a² (2ⁱⁱ)

Свойства дисперсии:

1. D(С)=0

2. D(С*x)= c² * D(x)

3. D(x_+y)= D(x)+ D (y)

4. D(x+c)= D(x)

среднее квадратическое отклонение CB Х называется корень квадратный из дисперсии этой CB Х ;

δ(х)=_√D(x)

Начальный и центральный моменты

Начальным моментом порядка K CB X называется МО величины x^k=M(x^k)*v_k

Замечание: Если К=1, то нач.момент первого порядка v₁=M(x)

К=2, то нач.момент первого порядка v₂=M(x²)

а)для ДСВ v_k =∑ x_i^k * p_i

б)для НСВ v_k =∫ x_i^k *f(x)dx- a^k

Центральным моментом порядка K CB X называется МО величины (x-M(x^k))

М^k=[(x-M(x))^k]

М_k=М[(x-M(x))^k]

Возьмем К=1, М=1, тогда

К=1, М₁=М[(x-M(x))]=0

K=2, М₂=М[(x-M(x))²]*D(x_k)

Замечание:

а) для ДСВ М_k =∑ (x_i –а)* p_i

б) для НСВ М_k =∫ (x-а)^k *f(x)dx

коэффициентом ассиметрии (скошенности) CB X наз-ся число А, равное отношению центрального момента к кубу среднего квадратического отклонения А = m3/q3(x)

коэффициентом эксцесса (островершинности) наз-ся число

Е = m4/q4(x) - 3

Модой ДСВ X (М₀(х)) наз-ся наиболее вероятное значение CB X

Модой НСВ Х (М₀(х)) с плотностью f(x) наз-ся значение CB X, при котором функция f(x) достигает максимума.

Медианой CB X (М_L(х))наз-ся такое значение CB X (x_p), для которого одинаково вероятно, что CB X примет значение < x_p или > x_p

P{x < x_p }= P{x > x_p }=½

41.Нормальное распределение.

Нормальное распределение непрерывной случайной величины X имеет место, если (плотность) распределения имеет вид:

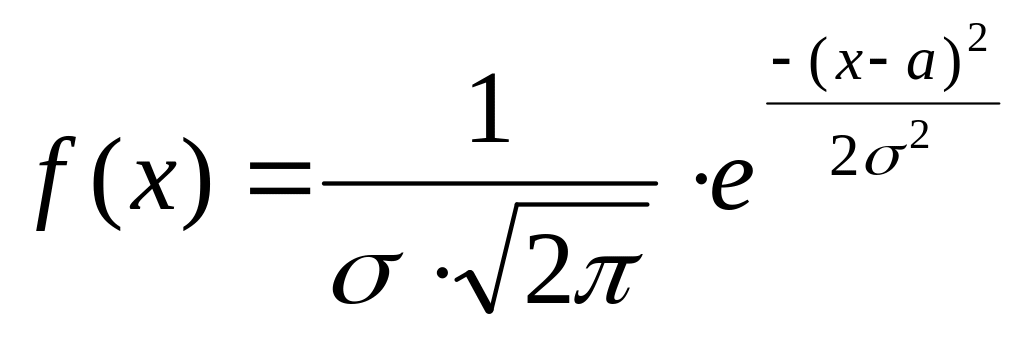, где a = M(x) (мат.ожидание), x (ср. кв. отклонение)

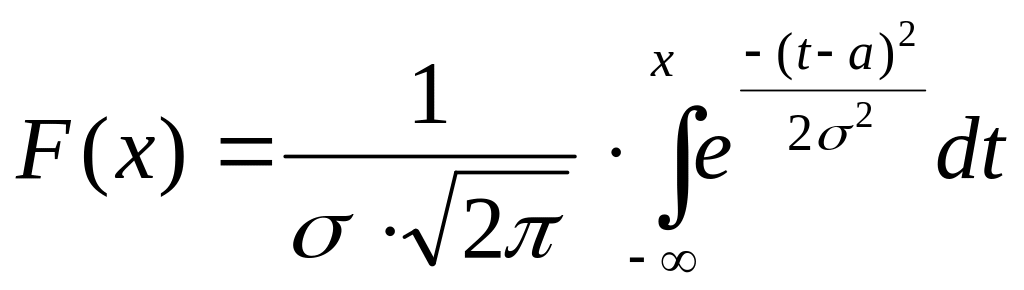
Нормальный закон распределения также называется законом Гаусса.

Можно заметить, что функция распределения F(x) является некоторой функцией . Эта функция имеет значения взаимосвязанные со значениями Лапласа.

Т.о. функция распределения для нормального распределения может быть вычислена с помощью формулы Лапласа.

Свойства:

1.Функция Лапласа является нечетной Ф(-x) = -Ф(x).

Значения функции Лапласа на :

Частным случаем нормального распределения, имеющие большие приложения, являются стандартные распределения.

a=0,=1.

Вероятность попадания нормального распределения случайной величины x в заданный интервал [] определяется формулой:

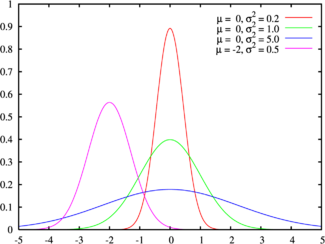
Плотность вероятности (Зелёная линия соответствует стандартному нормальному распределению)

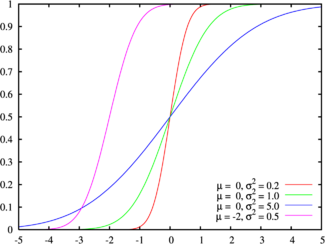
Функция распределения