24.Основные понятия булевой алгебры: булев куб, булевы функции.

Набор , где , , называется булевым (двоичным) вектором, а  – его компонентами (координатами). Для двух векторов и полагаем , если для всех .

Число называется весом (нормой) набора , а n называется его длиной. Каждому сопоставляется его номер . Несложно показать, что общее число двоичных наборов длины n равно .

Частично упорядоченное множество всех наборов называется n-мерным булевым (двоичным) кубом, а называется вершиной куба. Вершины, имеющие одинаковый вес k, образуют k-й слой булева куба.

Число называется расстоянием Хэмминга между вершинами и равно числу координат, в которых наборы и отличны друг от друга. Оно также равно минимальному числу ребер булева куба, по которым нужно пройти, чтобы дойти от вершины до .

Если , то вершины и называются соседними, а если для таких вершин , то вершина непосредственно предшествует . Если , то вершины и называются противоположными.

Функция называется функцией алгебры логики или булевой функцией. Множество всех булевых функций, зависящих от переменных , обозначается через , причем .

Элементарные булевы функции одной переменной определяет

Таблица 1 Элементарные булевы функции одной переменной

x	0	1	x
0	0	1	0	1
1	0	1	1	0

Таблица 2 Элементарные булевы функции двух переменных

		&					|
0	0	0	0	0	1	1	1	1
0	1	0	1	1	0	1	1	0
1	0	0	1	1	0	0	1	0
1	1	1	1	0	1	1	0	0

называется импликацией(читается "из следует ")

называется штрихом Шеффера (читается "не или не ")

называется стрелкой Пирса (читается "не и не ")

25.Элементарные булевы функции, их свойства. Существенные и фиктивные переменные. Основные функциональные элементы.

Таблица 1 Элементарные булевы функции одной переменной

x	0	1	x
0	0	1	0	1
1	0	1	1	0

Таблица 2 Элементарные булевы функции двух переменных

		&					|
0	0	0	0	0	1	1	1	1
0	1	0	1	1	0	1	1	0
1	0	0	1	1	0	0	1	0
1	1	1	1	0	1	1	0	0

называется импликацией(читается "из следует ")

называется штрихом Шеффера (читается "не или не ")

называется стрелкой Пирса (читается "не и не ")

Переменная (i-я координата набора ) булевой функции называется существенной, если можно указать такие два соседних по i-й координате двоичных набора, что значения функции на этих наборах различны. В противном случае, переменная называется фиктивной (несущественной). Две булевы функции называются равными, если одну из них можно получить из другой добавлением или удалением фиктивных переменных. Пусть булевы функции f₁(х₁,х₁) и f₂(х₁,х₂) заданы следующей таблицей истинности:

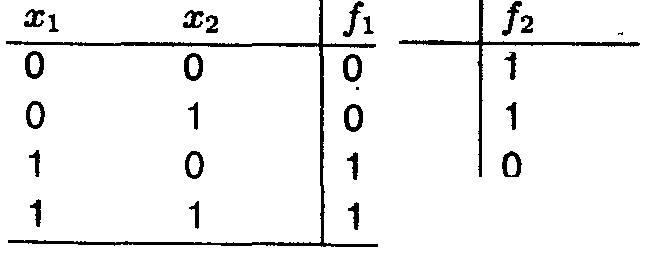
Для этих функций переменная х₁ — существенная, а переменная х₂ несущественная.

Техническая реализация элементарных функций основана на применении различных физических явлений. Для реализации функций алгебры логики используются базисные функциональные элементы, изображаемые в виде прямоугольников, причем инверсные входы и выход изображают пустыми кружками. В верхней части прямоугольника ставится знак, указывающий операцию: & – конъюнкция, 1 – дизъюнкция, M2 – сложение по ,  – эквивалентность.

Например, на рисунке 2 показан функциональный элемент Шеффера

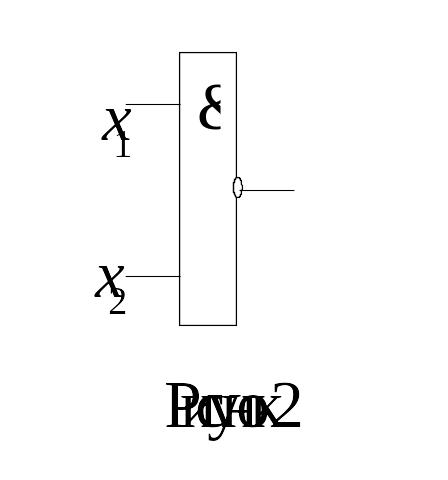
Более сложные элементы графически изображаются в виде композиции базисных функциональных элементов.