1.Множества, подмножества. Операции над множествами и их свойства. Диаграммы Эйлера – Венна

Множество – это совокупность объединенных по некоторым признакам различных объектов, называемых элементами множества. (Множества N натуральных чисел, Р – простых, Z - целых, К - вещественных)

Если объект х является элементом множества М, то говорят, что х принадле­жит М. (х   М).

Множество, не содержащее элементов, называется пустым .

Обычно в конкретных рассуждениях элементы всех множеств берутся из неко­торого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсумом).

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:

перечислением элементов: М: ={a₁,a₂,……,a_k}

характеристическим предикатом: М: = {х| Р(х)};

порождающей процедурой: М: = {x| x: = f}.

Характеристический предикат — это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение. Если для данного элемента условие выполнено, то он принадле­жит определяемому множеству, в противном случае — не принадлежит. Порождающая процедура — это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества.

Два множества X и Y равны, т. е. , если они состоят из одних и тех же элементов.

Если каждый элемент x множества X, является элементом множества Y, , то X называется подмножеством множества Y, Y – надмножеством X ( ).

Мощность множества М обозначается как |M|. Для конечных множеств мощ­ность — это число элементов. Например, | | = 0, но |{ }| = 1.

Операции над множествами

Для двух множеств X и Y определяются следующие основные операции:

объединение: ;

пересечение: ;

разность: ;

симметрическая разность: .

На рис. приведены диаграммы Эйлера, иллюстрирующие операции над мно­жествами.

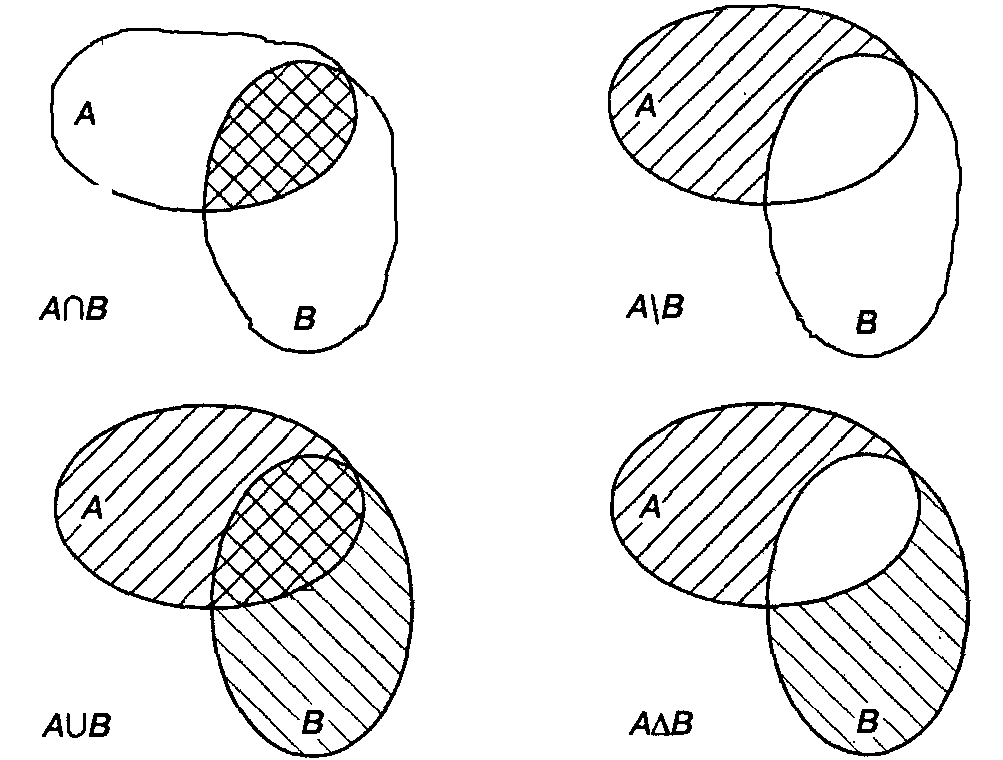
Свойства операций над множествами

Пусть задан универсум U. Тогда А, В, С U выполняются следующие свойства

В справедливости перечисленных свойств можно убедиться различными спо­собами. Например, нарисовать диаграммы Эйлера для левой и правой частей равенства.

2.Покрытия и разбиения множеств. Биномиальные коэффициенты и числа Стирлинга второго рода. Перечисление элементов множеств.

Разбиения и покрытия

Пусть — некоторое семейство подмножеств множества

Семейство £ называется покрытием множества М, если каждый элемент М при­надлежит хотя бы одному из Ее

Семейство £ называется дизъюнктным, если элементы этого семейства попарно не пересекаются, то есть каждый элемент множества М принадлежит не более чем одному из множеств Ее

Дизъюнктное покрытие £ называется разбиением множества М.

Пример

Пусть М: ={1,2,3}. Тогда {{1,2}, {2,3}, {3,1}} является покрытием, но не разби­ением; {{1}, {2}, {3}} является разбиением (и покрытием), а семейство {{1}, {2}} является дизъюнктным, но не является ни покрытием, ни разбиением.

Биномиальные коэффициенты

Число сочетаний С(m,n) — это число различных n-элементных подмножеств m-элементного множества. Числа С(m,n) встречаются в формулах решения многих комбинаторных задач.

Основная формула для числа сочетаний

позволяет получить следующие простые тождества.

Бином Ньютона

Числа сочетаний С(m,n) называются также биномиальными коэффициентами Смысл этого названия устанавливается следующей теоремой, известной также как формула бинома Ньютона¹.

Свойства биномиальных коэффициентов

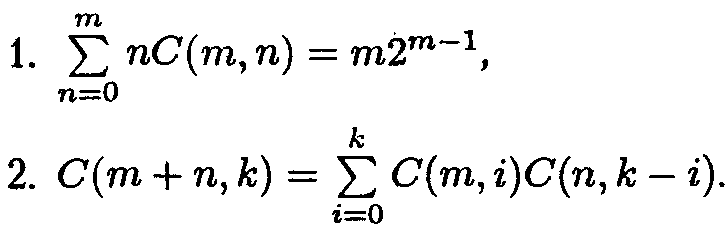
Из второй формулы вытекает эффективный способ реккурентного вычисления значений биномиальных коэффициентов, который можно предста­вить в графической форме, известной как треугольник Паскаля

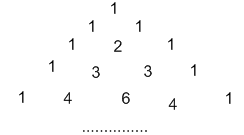
В этом равнобедренном треугольнике каждое число (кроме 1 на боковых сторонах) является суммой двух чисел, стоящих над ним. Число сочетаний C(m,n) находится в (m+1)-м ряду на (n+1)-м месте.

В комбинаторике числом Стирлинга второго рода S(n, k) называется число неупорядоченных разбиений n-элементного множества на k непустых подмножеств.

S(n,n) = 1, для n ≥ 0,

S(n,0) = 0, для n > 0,

для 0 < k < n.

Следующие простые правила служат основными инструментами в теории перечислений элементов множеств:

правило равенства – при взаимно однозначном соответствии между элементами конечных множеств X и Y имеет место равенство ;

правило суммы – для любого разбиения конечного множества имеет место равенство ;

правило произведения – для декартова произведения семейства конечных множеств имеет место равенство .