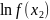МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное учреждение высшего профессионального образования

«Ижевский государственный технический университет им. М.Т.Калашникова»

Кафедра АСОИУ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине «Вычислительная математика»

на тему «Метод наименьших квадратов».

Выполнил

студент гр. Б03-782-1 ФИО

Руководитель

преподаватель кафедры АСОИУ А.Н.Соловьева

Ижевск 2012

СОДЕРЖАНИЕ

Y

ВВЕДЕНИЕ 3

1 Обзор существующих методов аппроксимации 4

2 Математическая постановка задачи аппроксимации функции 10

Введение

Метод наименьших квадратов – один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке различного рода измерений.

Метод наименьших квадратов был предложен К. Ф. Гауссом и А. Лежандром. Ныне способ представляет собой один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.

В большинстве экспериментальных данных, задаваемых с помощью табличной функции, имеется достаточно большой разброс точек. При этом использование кусочной или непрерывной интерполяции не всегда оправдано, поскольку ставится задача исследовать общую тенденцию изменения физической величины.

В этом общем случае аппроксимации искомая кривая не обязательно должна проходить через заданные точки. Предполагается использовать кривую, сумма квадратов отклонений в узловых точках минимальна. Именно в таких случая используется метод наименьших квадратов.

1. Обзор существующих методов аппроксимации

1. Общая постановка задачи метода наименьших квадратов

Пусть функция 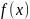принимает в точках 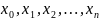значения . Аналитическое выражение функции при этом не известно, данные имеют неустранимую погрешность, а количество точек велико .

В таких случаях применение интерполяции (как, например, интерполяция полиномом Ньютона или интерполяция сплайнами) не приемлемо, т.к интерполяционные функции не будут отражать реального поведения функции.

В таких случаях находиться функция , которая проходит ближе всего к заданным точками, но не обязательно совпадает функцией в узловых точках. Из множества всех возможных функций выбирается такая, что сумма:

минимальна.

Вид функции зависит от конкретного набора точек. Обычно из набора точек, отмеченных в координатных осях, устанавливается примерная зависимость, а с помощью различных методов находятся коэффициенты функции.

2. Аппроксимация многочленами

Пусть дана экспериментальная таблица и требуется составить многочлен, степени не выше часто

Данный многочлен должен удовлетворять условию:

где 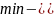минимум из всех возможных отклонений.

Графически это представлено на рисунке 1.1.

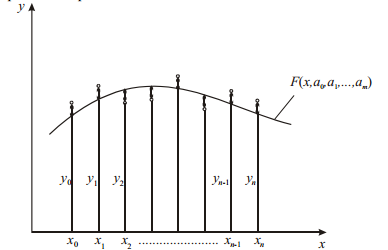
Рисунок 1.1 – Метод наименьших квадратов

Необходимым условием минимума функции многих переменных является равенство нулю ее частных производных первого порядка по независимым переменным. В функционале такими независимыми переменными являются коэффициенты многочлена, которые до их определения являются не постоянными, а варьируемыми переменными.

Неоднородная СЛАУ порядка относительно неизвестных является нормальной и, следовательно, ее матрица является симметричной и положительно определенной. Решения удовлетворяют условию наименьшего квадратичного отклонения.

Данную систему можно представить в виде:

и решив её, можно получить коэффициенты наилучшим образом сглаживающих функцию. Если в качестве взять , то полученный многочлен будет являться интерполяционным полиномом.

3. Аппроксимация прямой

В данном случае функция имеет вид , а коэффициенты находятся из условия, что

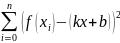
имеет наименьшее значение.

Для нахождения коэффициентов, необходимо решить следующую систему уравнений:

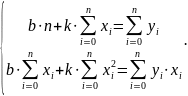
Решив данную систему методом Крамера, получим следующие выражения для нахождения :

4. Аппроксимация показательной функцией

Степенная зависимость имеет вид

Нахождение параметров показательной функции может быть сведено к нахождению коэффициентов линейной функции. Покажем это.

Прологарифмируем функцию, в результате чего получим равенство:

Введем новую переменную

тогда будет функцией от .

Обозначим:

в таком случае задача свелась к нахождению коэффициентов линейной функции

Для нахождения коэффициентов функции необходимо прологарифмировать значения и , т.е. из таблицы 1.1, получить таблицу 1.2.

Таблица 1.1 – Исходная таблица функции

Таблица 1.2 – Прологарифмированная таблица функции

После этого по таблице 1.2 необходимо найти параметры функции вида

После этого необходимо найти значение по следующей формуле:

То, что аргументы функции и значения функции нужно логарифмировать, налагает ограничение – все точки функции должны находится в первой четверти координатной оси.