13. Модель Джелинского-Моранды, Шика-Волвертона.

Модель Джелинского-Моранды. Допущения у модели:

1. Время до очередного отказа распределено по экспотенциальному закону

2. Все ошибки равновероятны и их появление не зависит друг от друга

3. Частота появления ошибок (функция риска, интенсивность отказа) пропорциональна числу не выявленных ошибок

λ(ti) = Kjm * [Eo – (i - 1)], где Eo – число ошибок в ПО до начального тестирования, Kjm – коэффициент Джелинского-Моранды, ti – интенсивность времение между i = 1 и i, обнаруженной ошибкой и число ошибок, обнаруженных к моменту отладки t.

4. λ(ti) постоянна на интервале между 2-мя смежными моментами появления ошибок

5. Каждая обнаруженная ошибка в ПО немедленно устраняется и число ошибок уменьшается на 1

6. Ошибки корректируются без внесения новых ошибок

Модель Шика-Волвертона. Дополнительно к модели Джелинского-Моранды используются:

1. Частота появления ошибок пропорциональна времени отладки программы ti:

λ(ti) = Kjm * [Eo – (i - 1)] * ti

14. Геометрическая модель.

В данной модели предполагается, что исходное число ошибок в программе – эта величина нефиксированная и все ошибки не равновероятны. Считается, что по мере отладки обнаруживать ошибки становится труднее. Т.о. ПО никогда не освобождается от ошибок.

Основные предпосылки этой модели:

1. Общее число ошибок неограниченно.

2. Обнаружение ошибок равновероятно.

3. Обнаружение ошибок – процесс независимый от ошибок.

4. ПО работает к условиям близким к реальным.

5. Интенсивность обнаружения ошибок образует геометрическую прогрессию, и она в интервале между появлениями ошибок постоянна.

λ(ti) = D * 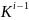, где λ(0) = D , D – исходное значение интенсивности отказа, К – константа пропорциональности, 0<K<1, ti – время между появлениями i-1 и i-ой обнаруженной ошибок.

Как правило, интенсивность геометрической модели определяется методом максимального правдоподобия.

15. Статистическая модель Миллса.

В программу заносится несколько известных ошибок S. Эти ошибки вносятся случайным образом. Затем делается предполжение, что вероятность обнаружения собственных ошибок и обнаруженных одинакова. Т.о., тестируя программу и отсортировывая собственные и внесенные ошибки, можно оценить превоначальное число ошибок в программе E₀:

Е₀ = S*n / V

S – количество внесенных ошибок

n – количество найденных собственных ошибок

V – число найденных внесенных ошибок.

Достоинства:

1) математически проста и интуитивно понятна;

2) психологическое ­–при обнаружении не всех внесенных ошибок тестирование вынуждено продолжаться.

Недостатки:

1) Процесс внесения ошибок, т.к. предполагается что чобственные и внесенные ошибки появляются с равной вероятностью. Т.о, вносимые ошибки должны быть типичны для этой программы.

16. Модель Нельсона.

В основе модели лежит представление программы в виде некоторой функции F(E_i), где E_i набор значений данных, необходимых для выполнения набора программы

E = {E_i|_{i = 1,2,…,N}} – число возможных наборов вх. данных

Выполнение (прогон) программы приводит к получению для каждого E_i определенного значения F(E_i). Наличие дефектов в программе приводит к тому, что получается некоторая F', отличная от F. Для некоторого E_i отклонение F’ от F находится в некоторых допустимых пределах ∆I, т.е. для получения премнемого результата необходимо выполнение сл.условия |F’(E_i) – F(E_i)| <= i

Множество наборов, не удовлетворяющих данному условию, образуют подмножество E_e и называется рабочими отказами.

Вероятность Q того, что прогон программы приведет к отказу равна вероятности, что набор входных данных E_i, используемый в данном прогоне, принадлежит множетсву E_e

Q = n_e/N, N – число возможных наборов значений входных данных,

n_e – число различных наборов значений, содержаихся в E_e

P = 1 – Q – вероятность удачного прохода.