Міністерство охорони здоровя України

львівський Національний медичний університет

Імені данила галицького

« Затверджено »

на методичній нараді

кафедри медичної інформатики .

Завідувач кафедри

професор Готра О.З._____________

«___»_____________ 2009 р.

Методичні рекомендації

для самостійної роботи студентів

при підготовці до практичного заняття

Навчальна дисципліна	Медична інформатика
Тема заняття 2:	Формальна логіка у вирішенні задач діагностики, лікування та профілактики захворювань.
Курс:	ІІ
Факультет:	Медичний

Львів - 2009

Актуальність теми. Використання телемедичних технологій відкриває нові унікальні можливості діагностики і лікування найрізноманітніших захворювань і патологічних станів. Використання віддаленого консультування і інших методів дозволяє економити час фахівців, матеріальні ресурси. На даному етапі розвитку вітчизняної структури телемедицини важливим є завдання розробки загальних структур, методичних вказівок і програмного забезпечення для національної телемедичної мережі.

Мета заняття: Інтерпретувати основні поняття формальної логіки. Аналізувати складені висловлення. Демонструвати вміння використовувати логічні функції для розвязання медико-біологічних задач

Базовий рівень підготовки. Елективний курс «Європейський стандарт компютерної грамотності. Володіти навичками роботи з програмним забезпеченням компютера: вміти завантажувати табличний процесор, вводити дані та формули до таблиць, виконувати елементарні операції над табличними.

Зміст навчального матеріалу Основи логіки висловлень

Освоєння логічної науки дає можливість свідомо будувати правильні міркування, відрізняти їх від неправильних, уникати логічних помилок, вміло і ефективно обґрунтувати істинність думок, захищати свої погляди і переконливо спростовувати хибні думки та неправильні міркування своїх опонентів, сприяє удосконаленню стихійно сформованої логіки мислення. Завдяки логіці людина прилучається до новітніх результатів логічних досліджень.

Логіка – наука про закони і форми мислення

Вислів – деяка пропозиція, яка може бути істинне (вірно) або помилково

Твердження – думка, яку потрібно довести або спростувати

Міркування – ланцюжок висловів або тверджень, певним чином зв'язаних один з одним

Висновок – логічна операція, в результаті якої з одного або декількох даних думок виходить (виводиться) нова думка.

Логічне висловлення – запис або усне твердження, в яке, разом з постійними, обов'язково входять змінні величини (об'єкти). Залежно від значень цих змінних логічне висловлення може приймати одне з двох можливих значень: ІСТИНА (логічна 1) або БРЕХНЯ (логічний 0)

У логіці висловлень має значення не зміст висловлень, а їхнє істинне значення, причому істинне значення складених висловлень теж визначається не за змістом складеного висловлення, а за істинними значеннями складових його висловлень.

Висловлення є простим (елементарним), якщо його неможливо розкласти на більш дрібні. Звичайно до них відносяться висловлення, що не містять логічних зв’язувань. Складне логічне висловлення – логічне висловлення , складене з одного або декількох простих (або складних) логічних виразів, зв'язаних за допомогою логічних операцій.

Алфавітом називається будь-яка не порожня множина символів будь-якої природи. Словом у даному алфавіті називається будь-яка кінцева послідовність (можливо порожня) символів даного алфавіту.

Алфавіт логіки висловлень містить наступні символи: букви А, В, С, …, X, Y, Z, … або букви з індексом – , що позначають висловлення; символи логічних операцій , , , , ; символи дужок ( , ).

Алгебра логіки - це математичний апарат, за допомогою якого записують, вираховують, спрощують і перетворюють логічні вислови.

Логічний вислів — це будь-яке висловлення, відносно якого можна однозначно сказати, істинно воно або хибне.

Так, наприклад, висловлення “6 — парне число” слід вважати за вислів, оскільки воно істинне. Висловлення “педіатрія – математична наука” теж вислів, проте воно помилкове.

Не всяке висловлення є логічним висловом. Висловами не є, наприклад, висловлення “учень десятого класу” і “інформатика - цікавий предмет”. Перше висловлення нічого не стверджує про учня, а друге використовує дуже невизначене поняття “цікавий предмет”. Питальні і окличні висловлення також не є висловами, оскільки говорити про їх істинність або помилковість не має сенсу.

Висловлення типа “в місті A більше мільйона жителів”, “у нього блакитні очі” не є висловами, оскільки для з'ясування їх істинності або помилковості потрібні додаткові відомості: про яке конкретно місті або людині йде мова. Такі пропозиції називаються висловлювальними формами.

Висловлювальна форма - це оповідна пропозиція, яка пряма або побічно містить хоч би одну змінну і стає висловом, коли всі змінні заміщаються своїми значеннями.

Алгебра логіки розглядує будь-який вислів тільки з однієї точки зору — чи є воно істинним або помилковим, проте інколи важко встановити істинність вислову. Так, наприклад, вислів “площа поверхні Індійського океану дорівнює 75 млн.кв.км.” в одній ситуації можна порахувати помилковим, а в іншій — істинним. Помилковим — оскільки вказане значення неточне і взагалі не є постійним. Істинним — якщо розглядувати його як деяке наближення, прийнятне на практиці.

Слова, що вживаються в звичайній мові, і словосполучення "ні”, “і”, “або”, “якщо..., то”, “тоді і тільки тоді” та інші дозволяють з вже заданих висловів будувати нові вислови. Такі слова і словосполуки називаються логічними зв'язками.

Вислови, утворені з інших висловів за допомогою логічних зв'язків, називаються складеними. Вислови, які не є складеними, називаються елементарними.

Т ак, наприклад, з елементарних висловів “Юкало — спортсмен”, “Юкало — двієчник” за допомогою зв'язку “і” можна отримати складений вислів “Юкало — спортсмен і двієчник”, що відповідає - “Юкало — спортсмен, який погано вчиться”.

За допомогою зв'язку “або” з цих же висловів можна отримати складений вислів “Юкало – спортсмен або двієчник”, що розуміється в алгебрі логіки як “Юкало або спортсмен, або двієчник, або і спортсмен і двієчник одночасно”.

Істинність або помилковість отримуваних таким чином складених висловів залежить від істинності або помилковості елементарних висловів.

Д ля звернення до логічних висловів - призначають імена. Хай через А позначений вислів “Пацієнт хворий на невиліковну хворобу”, а через В - вислів “Пацієнт проходить діагностування”. Тоді складений вислів “Пацієнт хворий на невиліковну хворобу і проходить діагностування” можна коротко записати як А і В. Тут “і” - логічний зв'язок, А, В - логічні змінні, які можуть набувати тільки два значення, - “істина” або “брехня”, що позначаються, відповідно, “1” і “0”

Висловлення за своїм змістом може бути проблемним, достовірним або умовним

Проблемне – це висловлення, в якому щось стверджується чи заперечується з певним ступенем припущення. Наприклад, “причиною головного болю є, мабуть, підвищений тиск”.

Достовірне – це висловлення, що містить знання, обґрунтовані та перевірені практикою. Наприклад, “ людина дихає киснем”.

Умовне – це висловлення, в якому відображається залежність того чи іншого явища від тих чи інших обставин і в якому підстава і наслідок з’єднуються за допомогою логічного сполучника “якщо … , то … ” Наприклад, “якщо діагноз інфаркт міокарда, то спостерігається порушення серцевого ритму». Отже в умовному висловленні треба розрізняти підставу і наслідок.

Кожний логічний зв'язок розглядається як операція над логічними висловами і має свою назву і позначення:

(1) Операція, що виражається словом “ні”, називається запереченням і позначається рискою над висловом. Вислів істинний, коли помилково, і помилково, коли A істинно. Приклад. “лікар - медичний працівник” (А); “лікар - не є медичний працівник” ( ).

(2) Операція, що виражається зв'язком “і”, називається кон'юнкцією (лат. conjunctio - з'єднання) або логічним множенням і позначається крапкою "• " (може також позначатися знаком &). Вислів А•В істинно тоді і тільки тоді, коли обидва вислови А і В істинні. Наприклад, вислів

“ 10 ділиться на 2 і 5 більше 3”

істинно, а вислови

“10 ділиться на 2 і 5 не більше 3”, “10 не ділиться на 2 і 5 більше 3”, “10 не ділиться на 2 і 5 не більше 3”

помилкові.

(3) Операція, яка виражається зв'язком “або” називається диз'юнкцією (лат. disjunctio — розділення) позначається знаком v (або плюсом). Вислів А v В помилково тоді і тільки тоді, коли обидва вислови А і В помилкові. Наприклад, вислів

“ 10 не ділиться на 2 або 5 не більше 3”

помилково, а вислови

“10 ділиться на 2 або 5 більше 3”, “10 ділиться на 2 або 5 не більше 3”, “10 не ділиться на 2 або 5 більше 3”

істинні.

(4) Операція, що виражається зв'язками “якщо ..., то”, “з ... слідує” називається імплікацією (лат. implico — тісно зв'язані) і позначається знаком ® або =>. Вислів А ® У помилково тоді і тільки тоді, коли А істинно, а В — помилково.

Я к імплікація зв'язує два елементарні вислови? Наприклад: “даний чотирикутник - квадрат” (А) і “біля даного чотирикутника можна описати коло” (В). Розгледимо складений вислів А ® В, що розуміється як “якщо даний чотирикутник квадрат, то біля нього можна описати коло”. Є три варіанти, коли вислів А ®В істинно:

1. А істинно і В істинно, то даний чотирикутник квадрат, і біля нього можна описати коло;

2. А помилково і В істинно, то даний чотирикутник не є квадратом, але біля нього можна описати коло (зрозуміло, це справедливо не для будь-якого чотирикутника);

3. A помилково і B помилково, то даний чотирикутник не є квадратом, і біля нього не можна описати коло.

Помилковий тільки один варіант: А істинно і В помилково, тобто даний чотирикутник є квадратом, але біля нього не можна описати коло.

У звичайній мові зв'язка “якщо ..., то” описує причинно-наслідковий зв'язок між висловами. В логічних операціях розглядається тільки їх істинність або помилковість. Інколи можуть виникати «абсурдні» імплікації, утворені висловами, абсолютно не зв'язаними за змістом. Наприклад, такими:

“ якщо студент — першокурсник, то в медицина – практична наука”

“якщо діагностичний центр — на вул..Пекарській, то пацієнт є здоровий”.

(5) Операція, що виражається зв'язками “тоді і тільки тоді”, "необхідно і достатньо” “... рівносильно ...”, називається еквівалентністю або подвійною імплікацією і позначається знаком <=> . Вислів А <=> В істинно тоді і тільки тоді, коли значення А і В збігаються.

Н априклад, вислови

“24 ділиться на 6 тоді і тільки тоді, коли 24 ділиться на 3”

“23 ділиться на 6 тоді і тільки тоді, коли 23 ділиться на 3”

істинні, а вислови

“24 ділиться на 6 тоді і тільки тоді, коли 24 ділиться на 5”, “21 ділиться на 6 тоді і тільки тоді, коли 21 ділиться на 3”

помилкові.

Вислови А і В, які утворюють складений вислів А « В, можуть бути абсолютно не зв'язані за змістом, наприклад: “три більше двох” (А), “пінгвіни живуть в Антарктиді” (В). Запереченнями цих висловів є вислови “три не більше двох” ( ), “пінгвіни не живуть в Антарктиді” ( ). Утворені з висловів А, В складені вислови A х В і х істинні, а вислови A х і х В - помилкові.

Імплікацію можна висловити через диз'юнкцію і заперечення:

А ® У = v В

Еквівалентність можна висловити через заперечення, диз'юнкцію і кон'юнкцію:

А <=> В = ( v В) • ( v А).

(6) Нерівнозначністю (виключення «АБО») двох висловлень A і В називається висловлення, істинне, коли істинні значення A і В не збігаються, і хибне – у протилежному випадку. Позначення: , і ін. (читається: «або А , або В », «чи А, чи В»; розуміється – у розділовому значені).

(6) Операцією Шеффера (штрих Шеффера) над висловленнями A і В називається висловлення ( ) (читається « і – несумісні»), які хибні тоді і тільки тоді, коли A і В обоє істинні.

Операцій заперечення, диз'юнкції і кон'юнкції достатньо, щоб описати і обробити логічні вислови.

Порядок виконання логічних операцій задається круглими дужками. Спочатку виконується операція заперечення (“ні”), потім кон'юнкція (“і”), після кон'юнкції - диз'юнкція (“або”) і в останню чергу - імплікація.

За допомогою логічних змінних і символів логічних операцій будь-який вислів можна формалізувати, тобто замінити логічною формулою.

Визначення логічної формули:

1. Всяка логічна змінна і символи “істина” (“1”) і “брехня” (“0”) — формули.

2. Якщо А і В — формули, то , (А • В), (А v В), (А ® B), (А <=> У) — формули.

3. Ніяких інших формул в алгебрі логіки немає.

Я к приклад розглянемо вислів “якщо я навчаюсь у медичному навчальному закладі, то стану медичним працівником”. Цей вислів формалізується у вигляді (A v B) ® C; така ж формула відповідає вислову “якщо студент навчається на відмінно, то він поступить в магістратуру”.

Як показує аналіз формули (A v B) ® C, при певних поєднаннях значень змінних A, B і C вона набуває значення “істина”, а при деяких інших поєднаннях - значення “брехня”. Такі формули називаються здійснимими.

Деякі формули набувають значення “істина” при будь-яких значеннях істинності що входять в них змінних. Такий буде, наприклад, формула А v , відповідна вислову “Цей трикутник прямокутний або гострокутний”. Ця формула істинна і тоді, коли трикутник прямокутний, і тоді, коли трикутник не прямокутний. Такі формули називаються тотожно дійсними формулами або тавтологіями. Вислови, які формалізуються тавтологіями, називаються логічно дійсними висловами.

Як інший приклад розгледимо формулу А • , якою відповідає, наприклад, вислів “У пацієнта виявлена саркома і пацієнт не є онкологічним хворим”. Очевидно, що ця формула помилкова, оскільки або А, або обов'язково помилково. Такі формули називаються тотожно помилковими формулами або суперечностями. Вислови, які формалізуються суперечностями, називаються логічно помилковими висловами.

Якщо дві формули А і В “одночасно”, тобто при однакових наборах значень що входять в них змінних, набувають однакових значень, то вони називаються рівносильними.

Рівносильність двох формул алгебри логіки позначається символом “=” або символом “º”. Заміна формули іншою, рівносильною, називається рівносильним перетворенням даної формули.

Роботу логічних елементів описують за допомогою таблиць істинності.

Таблиця істинності - це табличне представлення логічної схеми (операції), в якому перераховані всі можливі поєднання значень істинності вхідних операндів разом із значенням істинності вихідного сигналу (результату операції) для кожного з цих поєднань.

С х е м а   І

x	у	x Схема І реалізує кон'юнкцію двох і більше логічніших значень. Одиниця на виході схеми І буде тоді і тільки тоді, коли на всіх входах будуть одиниці. Коли хоч би на одному вході буде нуль, на виході також буде нуль. Зв'язок між виходом z цієї схеми і входами x і у описується співвідношенням: z = x•y (читається як "x і у"). •y
0	0	0
0	1	0
1	0	0
1	1	1

С х е м а   АБО

x	у	x v у
0	0	0
0	1	1
1	0	1
1	1	1

Схема АБО реалізує диз'юнкцію двох і більше логічніших значень.

Якщо принаймні на одному вході схеми АБО буде одиниця, на її виході також буде одиниця.

С х е м а   НЕ

x
0	1
1	0

Схема НЕ (інвертор) реалізує операцію заперечення.

Якщо на вході схеми 0, то на виході 1. Коли на вході

1, на виході 0.

С х е м а   І - НЕ

x	у
0	0	1
0	1	1
1	0	1
1	1	0

Схема І-НЕ складається з елементу І і інвертора і здійснює заперечення результату схеми І.

С х е м а   АБО - НІ

Схема АБО-НІ складається з елементу АБО і інвертора і здійснює заперечення результату схеми АБО.

x	у
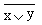
0	0	1
0	1	0
1	0	0
1	1	0

Все в одній таблиці:

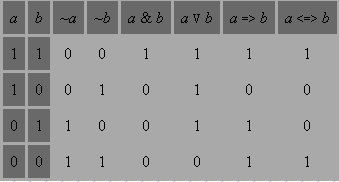
ОСНОВНІ ЗАКОНИ АЛГЕБРИ ЛОГІКИ

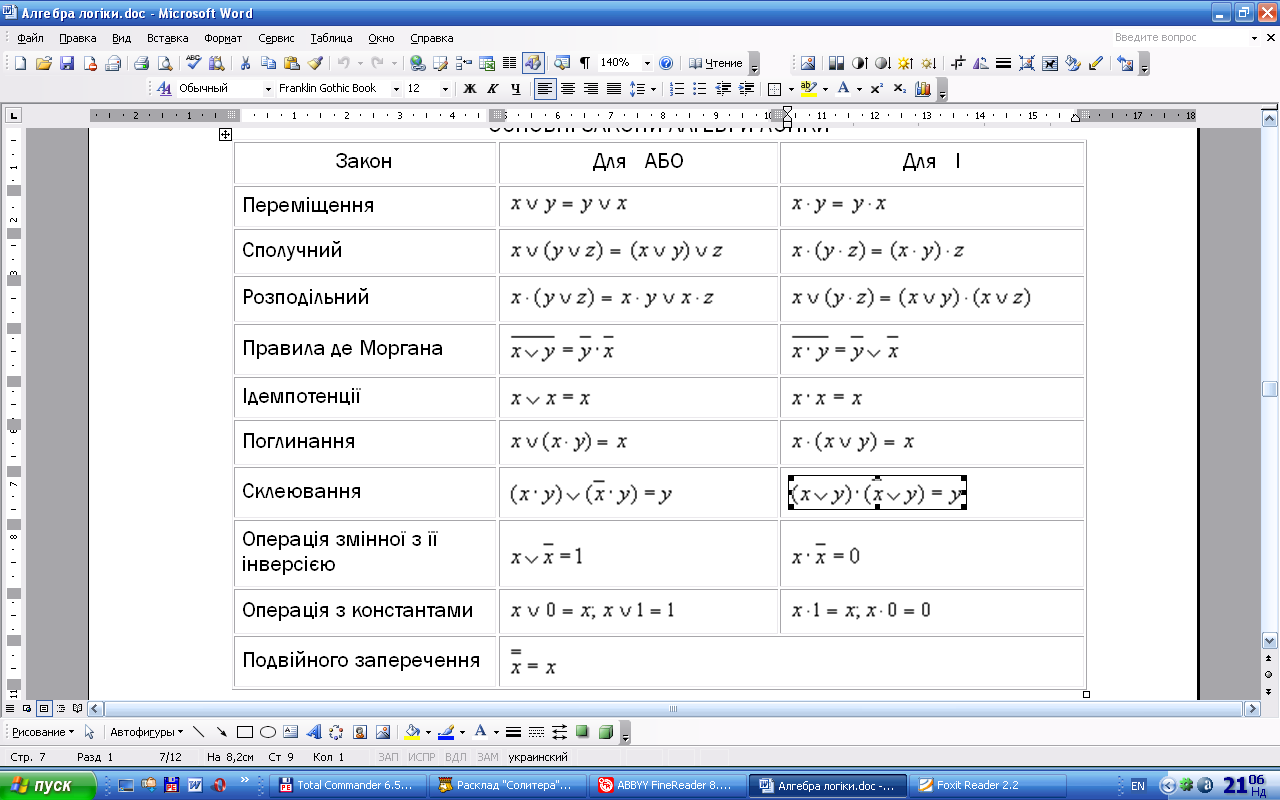
Згідно визначенню, таблиця істинності логічної формули виражає відповідність між всілякими наборами значень змінних і значеннями формули.

Для формули, яка містить дві змінні, таких наборів значень змінних всього чотири: (0,0),   (0,1),   (1,0),   (1,1).

Якщо формула містить три змінні, то можливих наборів значень змінних вісім:

(0,0,0),   (0,0,1),   (0,1,0),   (0,1,1),

(1,0,0),   (1,0,1),   (1,1,0),   (1,1,1).

Кількість наборовши для формули з чотирма змінними рівно шістнадцяти і так далі

Зручною формою запису при знаходженні значень формули є таблиця, що містить окрім значень змінних і значень формули також і значення проміжних формул.

Складемо таблицю істинності для формули, яка містить дві змінні x і у. По-перше, у двох стовпцях таблиці запишемо чотири можливі пари значень цих змінних, в подальших стовпцях — значення проміжних формул і в останньому стовпці — значення формули. В результаті отримаємо таблицю:

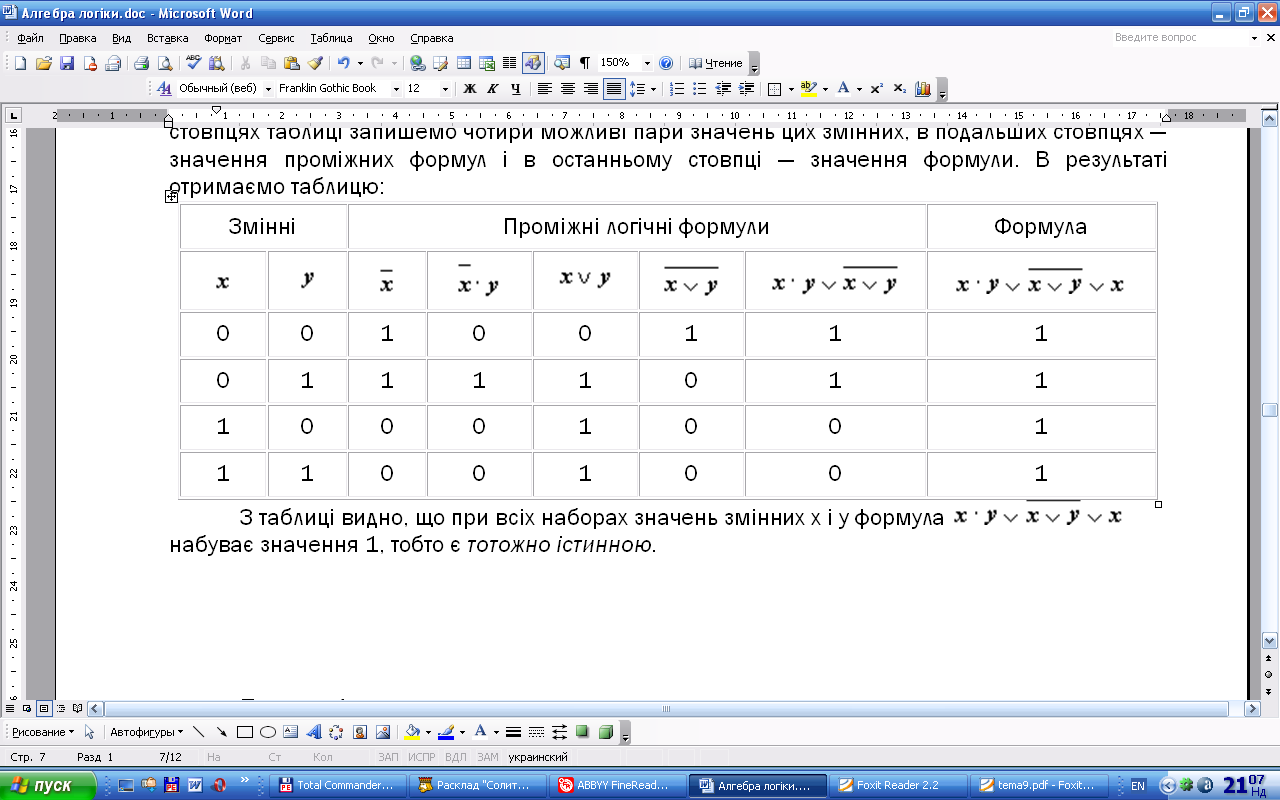
З таблиці видно, що при всіх наборах значень змінних x і у дана формула набуває значення 1, тобто є тотожно істинною.

Приклад 1:

Таблиця істинності для формули :

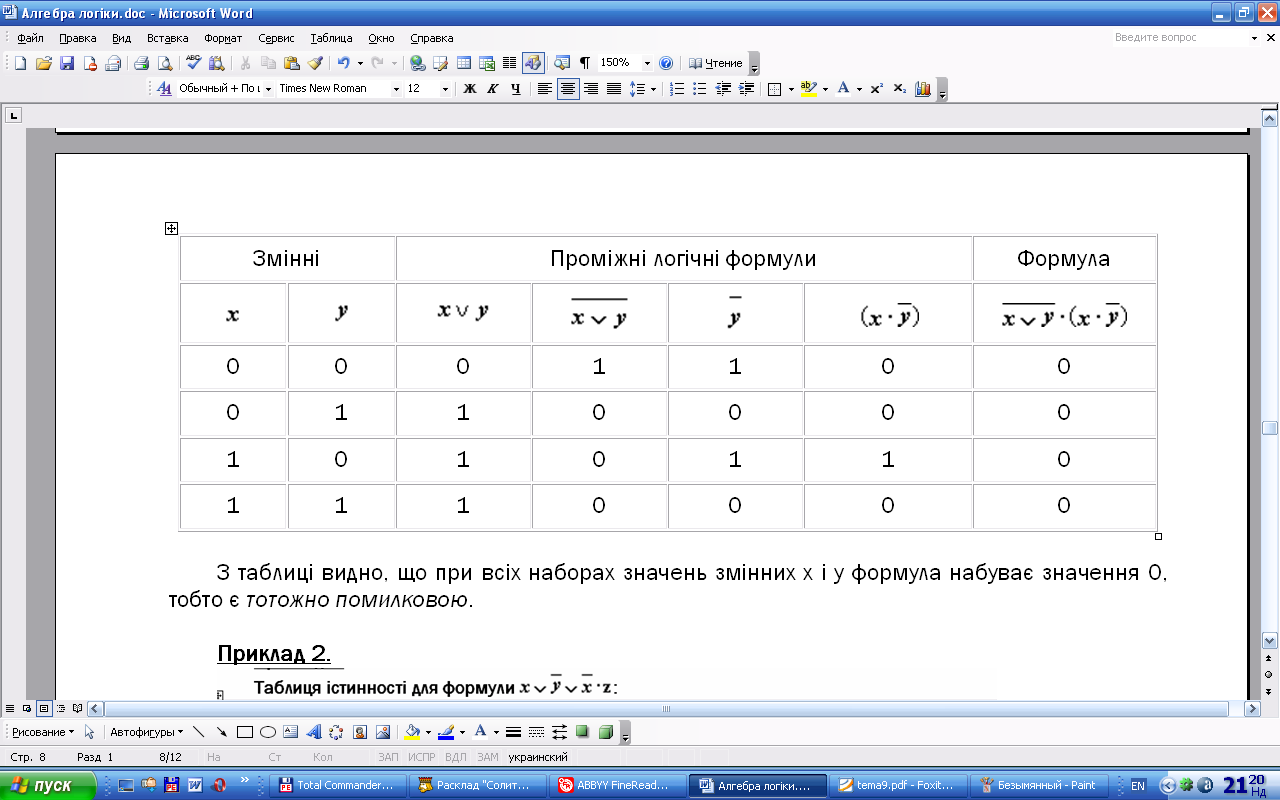
З таблиці видно, що при всіх наборах значень змінних x і у формула набуває значення 0, тобто є тотожно помилковою.

Приклад 2.

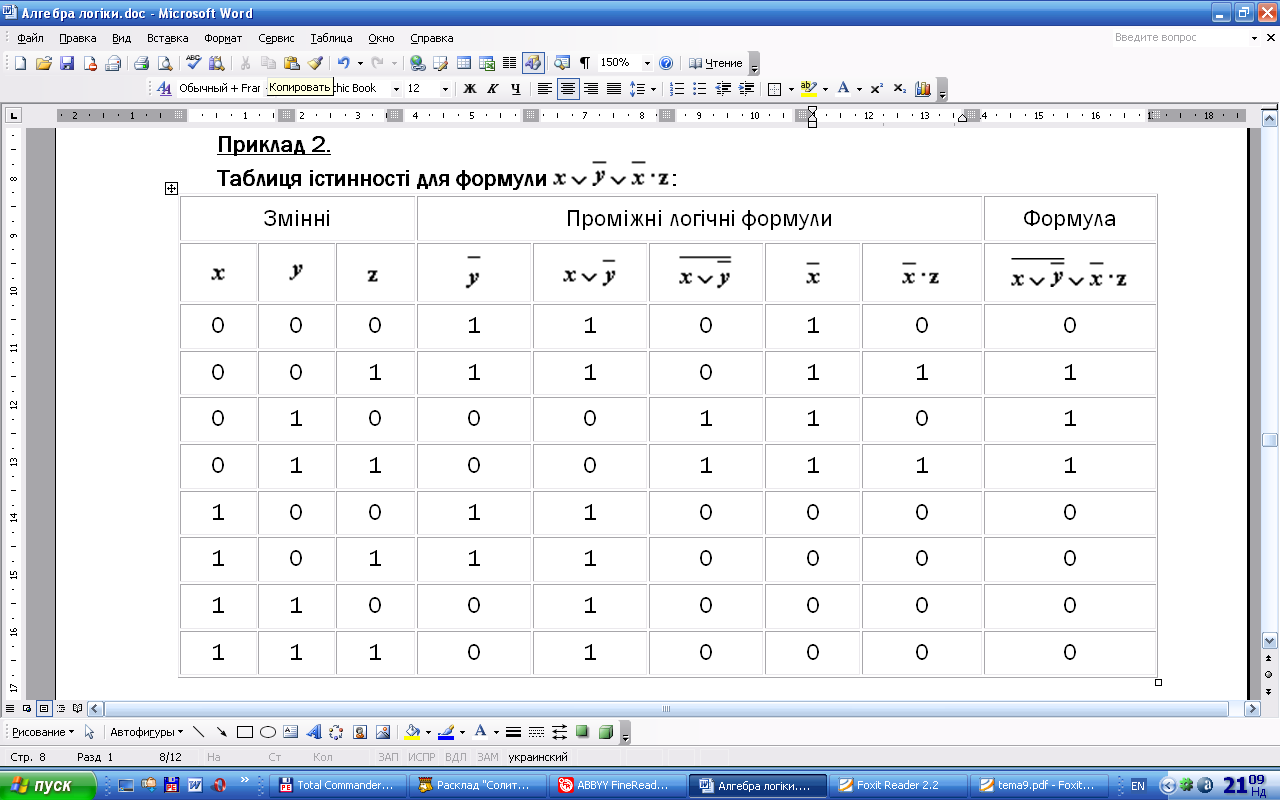
З таблиці видно, що формула в деяких випадках набуває значення 1, а в деяких — 0, тобто є здійснимою.