
- •Предисловие
- •Раздел 1 аксонометрические проекции
- •I Общие сведения
- •2 Стандартные аксонометрические проекции
- •2 Прямоугольные аксонометрические проекции. А Прямоугольная изометрия
- •Б Прямоугольная диметрия
- •4 Косоугольные аксонометрические проекции а Косоугольная фронтальная изометрия
- •Б Косоугольная горизонтальная изометрия
- •В Косоугольная фронтальная диметрия
- •5 Построение аксонометрической проекции окружности
- •6 Последовательность построения аксонометрических проекций объекта
- •7 Примеры построения аксонометрии
- •Вопросы для самопроверки
- •Упражнения
- •Раздел 2 Построение теней в аксонометрии
- •8 Общие сведения
- •9 Правила построения теней в аксонометрии а Тень точки
- •Б Тень прямой параллельной плоскости
- •В Тень прямой перпендикулярной плоскости
- •Г Тень прямой линии общего положения
- •10 Примеры построения теней в аксонометрии
- •Вопросы для самопроверки
- •Упражнения
- •Список рекомендованной литературы
- •Содержание
- •Раздел 1 Аксонометрические проекции . . . . . . . . . . . . . . . . . . 6
- •Раздел 2 Построение теней в аксонометрии . . . . . . . . . . . . . . 40
- •Приложение а варианты зданий
- •Приложение б примеры построения аксонометрии
Б Прямоугольная диметрия
В прямоугольной диметрической проекции коэффициент искажения по координатной оси У' принимают в два раза меньше, нежели по другим – kу = 0,5kх = 0,5kz, что приводит к таким коэффициентам: kх = kz ≈ 0,94, kу≈ 0,47. Поэтому стандартом разрешается использование приведенной проекции с коэффициентами искажения kх = kz= 1, а kу =0,5. В этой аксонометрической проекции угол между координатными осями Х' и Z' составляет 970 10', а между осями У' и Z' – 1310 25' (рис.9).
Поскольку kх
=
kz,
то плоскость
аксонометрических проекций
П' наклонена
под одинаковыми углами к координатным
осям Х и
Z пространственной
системы координат. Поэтому параметры
эллипсов, в которые проецируются
окружности, плоскости которых параллельны
г
Рис. 9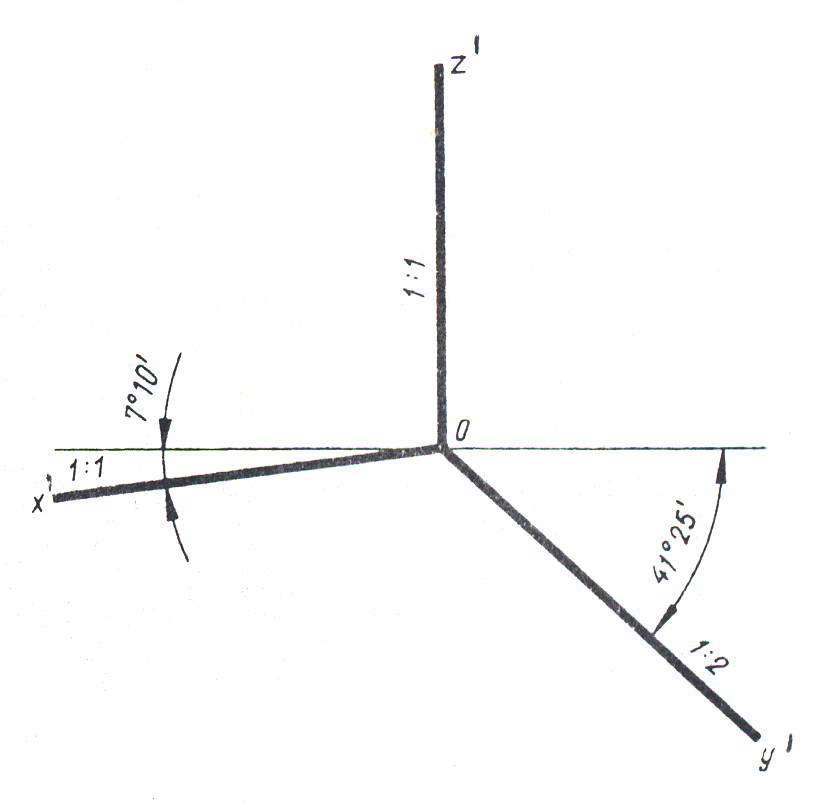 оризонтальной
и профильной плоскостям проекций, б
оризонтальной
и профильной плоскостям проекций, б
А параметры эллипсов в которые проецируются окружности, плоскости которых параллельны фронтальной плоскости проекций, будут равны: 2а=1,06D и 2в = 0,95D (для практической работы стандарт рекомендует брать малую ось эллипса 2в = 0,95D). Ориентация большой оси эллипса определяется аналогично изометрической проекции.
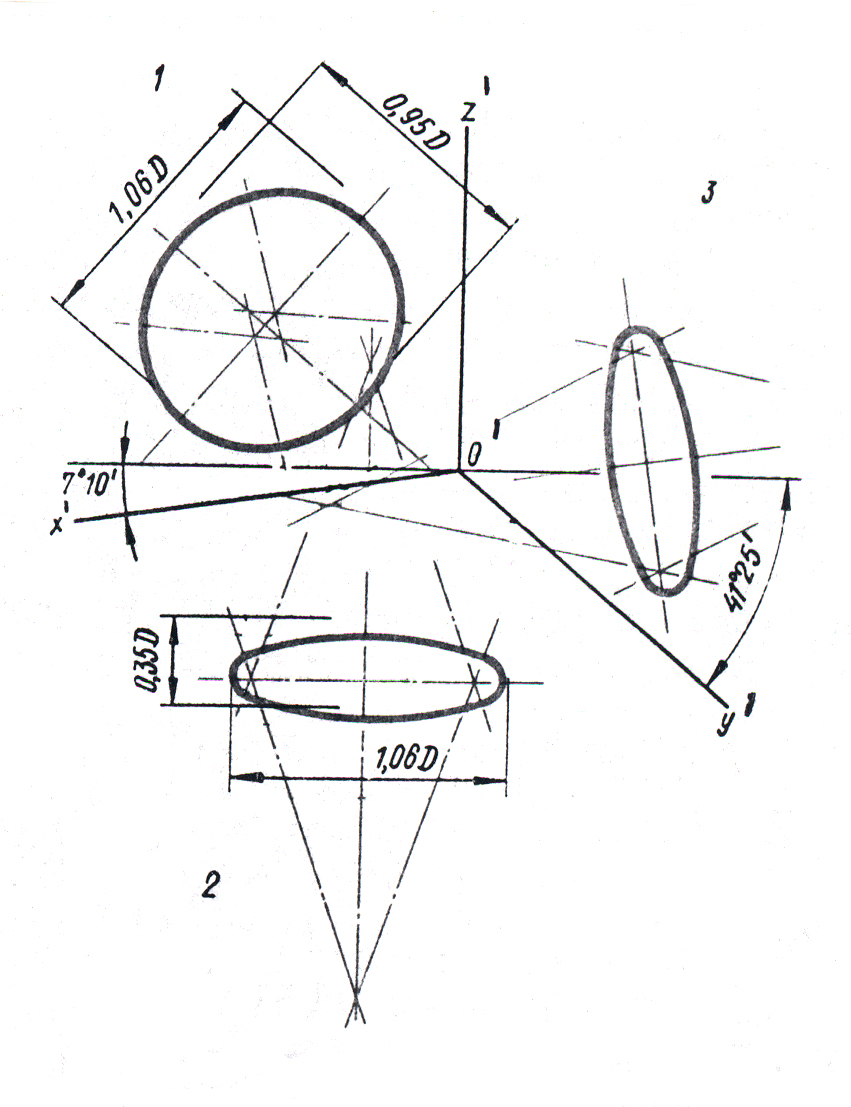
Рис. 10
В ряде случаев, оригиналы могут содержать значительное количество окружностей, плоскости которых параллельны той или иной плоскости проекций. В этих случаях трудоемкость построения прямоугольных аксонометрических проекций существенно возрастает за счет построения значительного количества эллипсов, в которые проецируются эти окружности. Поэтому нужны аксонометрические проекции, в которых такие окружности проецировались бы без искажения. Этому требованию отвечают косоугольные проекции.
4 Косоугольные аксонометрические проекции а Косоугольная фронтальная изометрия
Косоугольная фронтальная изометрия применяется в основном тогда, когда изображаемый предмет имеет большое количество окружностей или других кривых линий, расположенных во фронтальной плоскости.
При этой системе аксонометрических проекций аксонометрическая плоскость проекций располагается параллельно координатной плоскости проекций пространственной системы координат.
А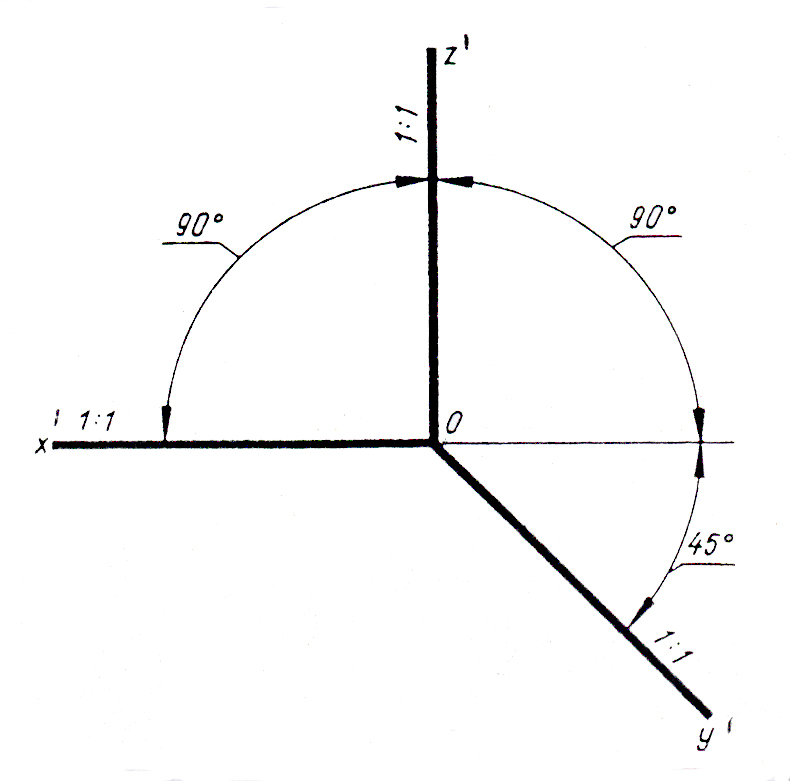 ксонометрическая
проекция, у которой плоскость
аксонометрических проекций П'
параллельна фронтальной плоскости
проекций и угол проецирования 450,
дает возможность получить косоугольную
фронтальную изометрическую проекцию
(рис.11). Иногда ее называют «кавальерная».
ксонометрическая
проекция, у которой плоскость
аксонометрических проекций П'
параллельна фронтальной плоскости
проекций и угол проецирования 450,
дает возможность получить косоугольную
фронтальную изометрическую проекцию
(рис.11). Иногда ее называют «кавальерная».
У
Рис. 11
12 + 12 + 12 = 2 + ctg2φ,
откуда ctg φ = 1 и φ = 450.
О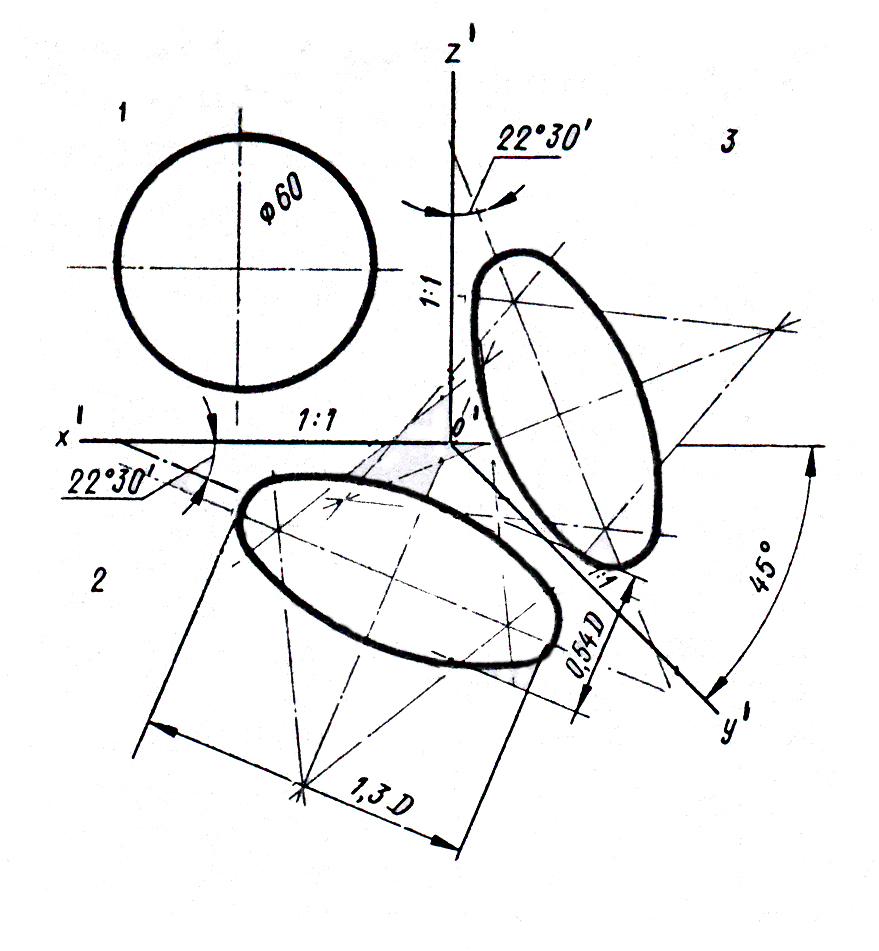 кружности,
лежащие в плоскостях, параллельных
фронтальной плоскости проекций,
проецируются на картинную плоскость
П'
в виде окружности, а окружности, лежащие
в плоскостях, параллельных горизонтальной
и профильной плоскостям проекций, в
виде эллипсов, большие оси которых
направлены под углом 22030'
по отношению к оси Х'
на горизонтальной плоскости и по
отношению к оси Z'
на профильной плоскости. Большая ось
эллипса на обеих плоскостях будет равна
1,3D,
а малая – 0,54D,
где D
– диаметр окружности (рис .12).
кружности,
лежащие в плоскостях, параллельных
фронтальной плоскости проекций,
проецируются на картинную плоскость
П'
в виде окружности, а окружности, лежащие
в плоскостях, параллельных горизонтальной
и профильной плоскостям проекций, в
виде эллипсов, большие оси которых
направлены под углом 22030'
по отношению к оси Х'
на горизонтальной плоскости и по
отношению к оси Z'
на профильной плоскости. Большая ось
эллипса на обеих плоскостях будет равна
1,3D,
а малая – 0,54D,
где D
– диаметр окружности (рис .12).
Рис. 12
