2 Стандартные аксонометрические проекции

Из сущности аксонометрических проекций вытекает, что, изменяя направление проецирования и положение аксонометрической плоскости проекций для каждого оригинала, можно получить бесчисленное множество аксонометрических проекций. Это предположение нашло свое подтверждение в теореме Польке-Шварца: любой полный плоский четырехугольник, который не вырождается, можно считать параллельной проекцией тетраэдра, заведомо заданной формы. Среди бесчисленного множества тетраэдров, проекции которых отвечают четырехугольнику А' В' С' D', (рис.5) есть и такой, у которого три ребра АВ, АС и АD взаимно перпендикулярны и равны друг другу. Эти три ребра можно принять за направление осей декартовой системы координат, на которых отложены натуральные единицы измерений. Тогда отрезки А'В', А'С' и А'D' можно принять за аксонометрические оси координат, на которых отложены масштабы (аксонометрические единицы измерения).

Т

Рис. 5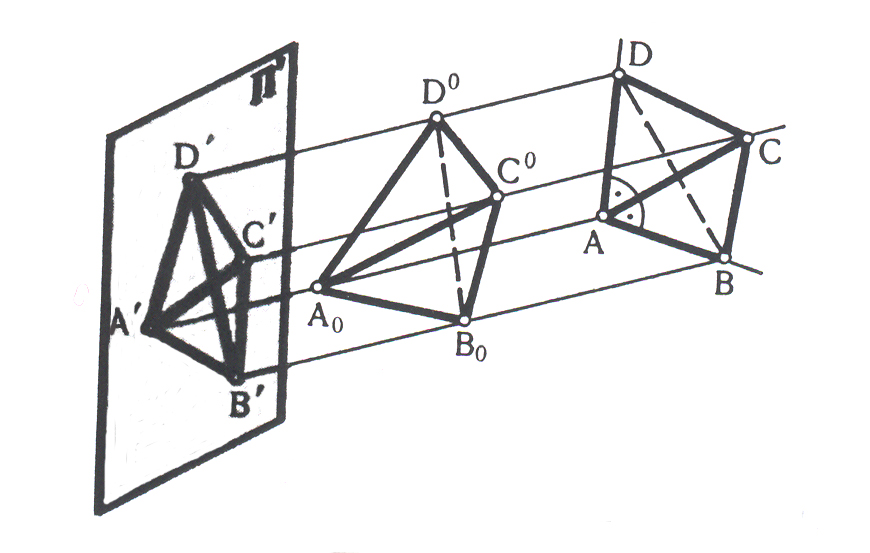

аким образом, любые три отрезка на плоскости, выходящие из одной точки, можно рассматривать как параллельные проекции трех равных и взаимно перпендикулярных отрезков в пространстве. Эта теорема носит название «Основного предложения аксонометрии». Впервые ее сформулировал К. Польке, а позднее обобщил Г. Шварц. На основании этой теоремы при построении аксонометрического изображения дается свобода выбора осей и аксонометрических масштабов.

Учитывая то, что доказательство этой теоремы выходит за пределы курса начертательной геометрии, приведем только вывод, который вытекает из нее: всегда найдется такое положение прямоугольной системы координат в пространстве и такой размер натурального масштаба по осям, а также такое направление проецирования, что любая аксонометрическая система окажется параллельной проекцией натуральной системы.

Возможность построения бесчисленного количества аксонометрических проекций для одного и того же оригинала является не столько преимуществом, сколько недостатком. Действительно, перед исполнителем сразу же возникает вопрос: какую аксонометрическую проекцию выбрать в том или ином случае? Разумеется ту, которая обеспечивает наибольшую наглядность. Но их множество.

Поэтому для наведения порядка в этом вопросе, необходимо ввести некоторые ограничения. Эти ограничения нашли свое отражение в ГОСТ 2.317-69 «Аксонометрические проекции» стандартов ЕСКД – Единая Система Конструкторской Документации. В соответствии с ним при выполнении чертежей для всех отраслей промышленности и строительства разрешается использовать только пять аксонометрических проекций, которые получили название стандартных: две прямоугольные (изометрическая и диметрическая) и три косоугольные (фронтальная и горизонтальная изометрические и фронтальная диметрическая).

2 Прямоугольные аксонометрические проекции. А Прямоугольная изометрия

Прямоугольная изометрическая проекция – наиболее простой вид прямоугольной аксонометрии. В прямоугольной изометрической проекции:

k_х = k_у = k_z = k, а поскольку φ = 90⁰, то 2 k² = 2, откуда k = √⅔ ≈ 0,82. Однако дробные коэффициенты искажения не удобны для практического применения, поэтому стандартом разрешается использовать, так называемые приведенные коэффициенты искажения k_х = k_у = k_z = 1, что дает так называемую приведенную изометрическую проекцию.

При использовании приведенных коэффициентов искажения аксонометрическое изображение пропорционально увеличивается в 1,22 раза по сравнению с оригиналом изображения. (1 : 0,82 ≈ 1,22). Однако выигрыш за счет простоты построения оправдывает этот недостаток.

Поскольку коэффициенты искажения по всем осям одинаковые, то аксонометрическая плоскость проекций имеет одинаковый угол наклона ко всем осям (и плоскостям проекций) пространственной системы координат, откуда следует, что углы между аксонометрическими осями также одинаковы и равны 120⁰ (рис.6). При этом заметим, что ось z' для всех стандартных аксоно-метрических проекций распола-гается вертикально.

И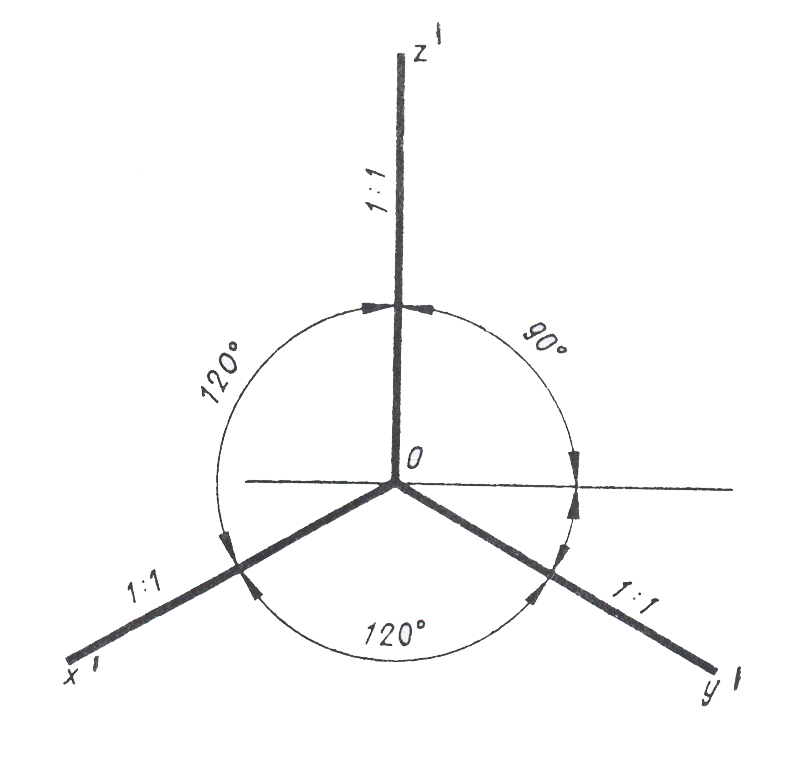 з равенства коэффициентов искажения также следует, что параметры эллипсов и их ориентация относительно аксонометрических осей будут одинаковыми.

У

Рис. 6

становлено, что для приве-денной изометрической проекции значение большой оси эллипса 2а = 1,22D, малой – 2в = 0,71D (где D – диаметр окружности), рис. 7.

Большая ось эллипса всегда перпендикулярна одной из аксонометрических осей. А какой именно, зависит от положения в пространстве плоскости окружности до проецирования.

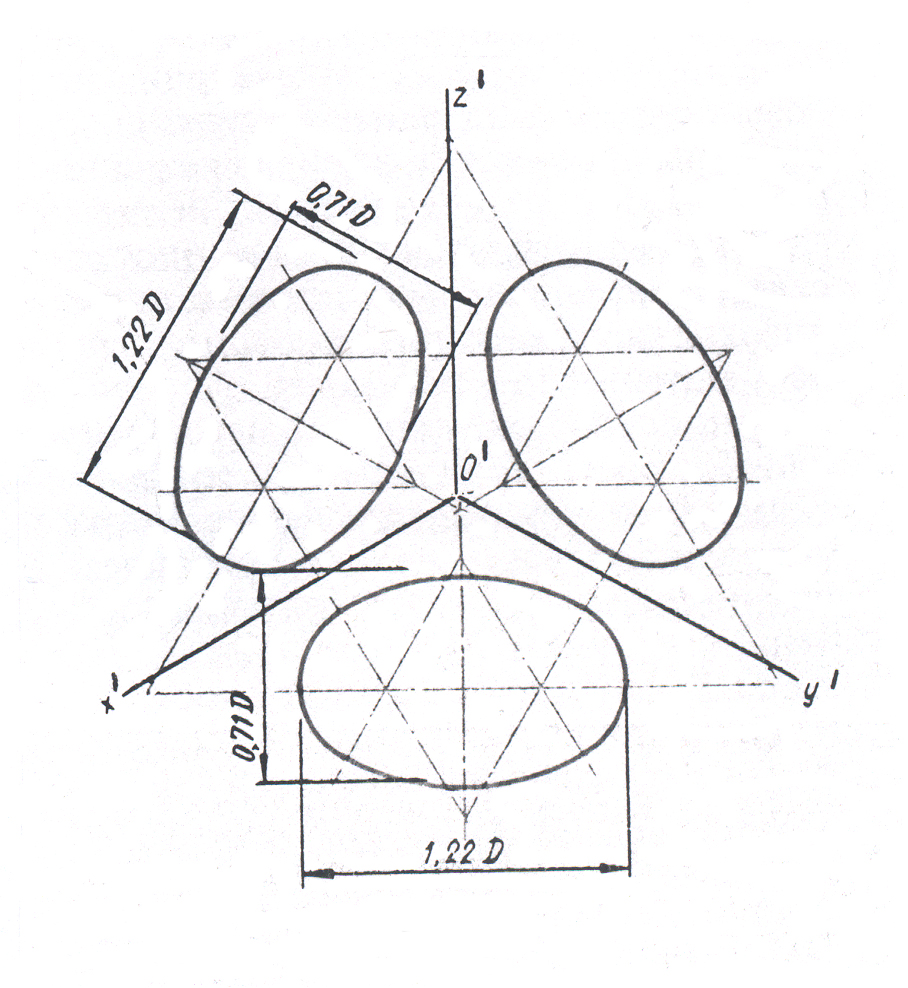
Рис. 7

Если плоскость окружности была перпендикулярна координатной оси Z, то большая ось эллипса будет перпендикулярна аксонометрической оси Z', если оси У, то У', если оси Х, то оси Х'.

Размеры осей эллипса для изометрической проекции можно определить графически (рис.8). Для этого проводим две взаимно перпендикулярные оси, чертим вокруг центра О окружность заданного диаметра.

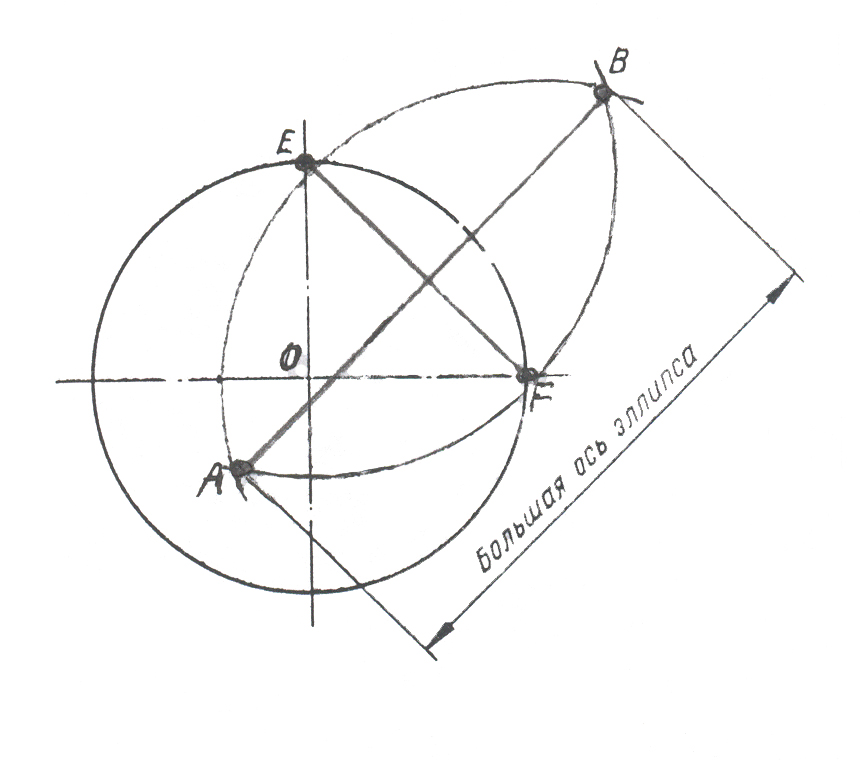
Рис. 8

Из точек E и F делаем засечки радиусом EF, которые пересекаются в точках А и В. Соединяя точки А и В, получим большую ось эллипса, равную 1,22D, а соединяя точки E и F, получим малую ось равную 0,7D.