2.3.Метод Ньютона-Рафсона
Предположим, что уравнение
имеет единственный корень
на отрезке
,
и производная
на этом отрезке существует, непрерывна
и отлична от нуля.
Тогда разложим функцию в ряд Тейлора (т.е. осуществим линеаризацию):
Причём точность приближения увеличивается
при
.
Дальше вместо исходного уравнения мы будем решать это приближённое уравнение:
Разрешив его относительно , получим:
Основная формула метода Ньютона-Рафсона имеет вид:
Метод Ньютона-Рафсона хорош тем, что использует более точные знания о поведении функции и поэтому сходится гораздо быстрее, чем метод простой итерации.
Формула Ньютона-Рафсона и сам метод имеет следующую геометрическую интерпретацию:
В точке
график
заменяется на касательную.Точка пересечения касательной с осью
принимается за новое приближение
.
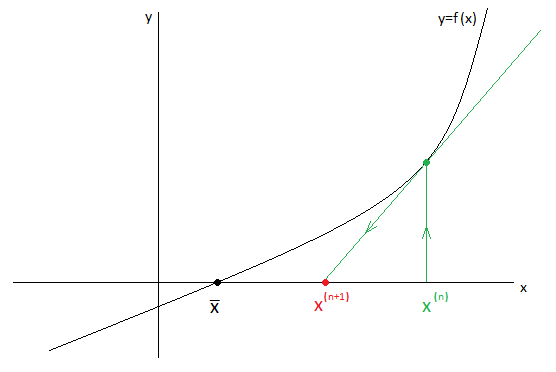
Далее строится точка
,
в которой снова строится касательная.
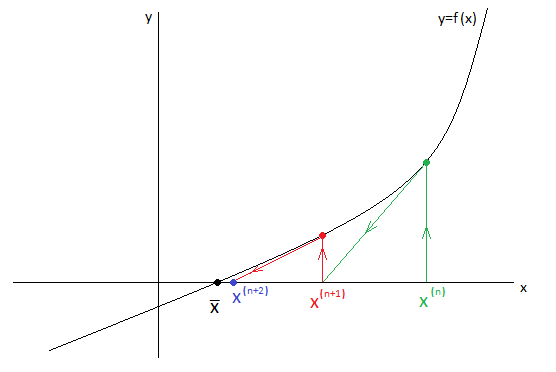
И так далее до тех пор, пока не будет достигнута заданная точность.
Обоснование.
Будем обозначать отрезок
как
.
Тогда тангенс угла наклона, или производная
в точке касания будет равна
,
значит
.
С учётом формулы Ньютона-Рафсона:
.
Примечание 1.
Формулу Ньютона-Рафсона можно интерпретировать следующим образом.
Предположим, что
.
Тогда перейдём от уравнения
к равносильному уравнению
,
и на основании формулы Ньютона-Рафсона
это будет означать, что:
Применительно к уравнению вида метод Ньютона-Рафсона реализует схему метода простых итераций. При этом:
Тогда по определению следует, что
Примечание 2.
Насчёт скорости сходимости. Если точку
выбрать
достаточно близкую к
,
то скорость убывания погрешности
здесь выше, чем в методе простой итерации.
Там скорость сходимости линейная, здесь
– квадратичная.
Примечание 3.
Но есть и такие случаи, когда очень близкое приближение может привести к бесконечному циклу – бывают и такие крайне выпуклые функции.
Лекция 3. Вычисление алгебраического полинома.
Большое прикладное значение имеет задача вычисления алгебраического полинома:
Напомним, что полином степени n имеет ровно n корней, как и действительных, так и комплексных.
Для того, чтобы вычислить корни таких уравнений можно с успехом применять итерационные процедуры, например метод Ньютона-Рафсона. Но их применение чаще всего приводит к выполнению множества действий, что может привести к потере точности и увеличению времени работы.
Один из эффективных способов вычисления алгебраического полинома – использование схемы Горнера.
3.Схема Горнера
Рассмотрим этот метод на примере полинома пятого порядка:
Предположим, что
-
корень этого многочлена. Тогда исходный
полином можно представить в виде:
,
где между коэффициентами a и b есть связь. Вычислим её. Раскрыв скобки, и сгруппировав известные и неизвестные величины, получим:
Теперь приравняем соответствующие коэффициенты a и b между собой:
Разрешим эту систему относительно коэффициентов b:
Обратите внимание, что у нас получилась явная рекуррентная последовательность: результат каждой строчки подставляется в следующую.
В общем виде рекуррентность выглядит так:
А правило Горнера в общем виде записывается так:
Обратите внимание, что схема Горнера не решает многочлен, а только удобно вычисляет его значения. Для решения с помощью схемы Горнера используется модифицированный метод Ньютона-Рафсона.