-72-

Серов В.А.

Вычислительные методы и алгоритмы

Учебное пособие

Москва, 2012

Оглавление

Серов В.А. 1

Вычислительные методы и алгоритмы 1

Учебное пособие 1

Москва, 2012 1

Лекции 1-2. Численные решения нелинейных уравнений 3

1. Локализация корней 3

2. Итерационное уточнение корней 10

2.1. Метод бисекции 10

2.2. Метод простой итерации 13

2.3. Метод Ньютона-Рафсона 21

Лекция 3. Вычисление алгебраического полинома. 24

3. Схема Горнера 24

4. Метод Бирге-Виета 25

Лекция 4-5. Решение СЛАУ 28

5. Метод Гаусса 28

6. Метод Гаусса-Зейделя 33

Лекция 6. Нормы векторов и матриц 38

7. Норма вектора 38

8. Абсолютная и относительная погрешности вектора 39

9. Норма матрицы 40

Лекция 7. Обусловленность вычислительной задачи 43

10. Число обусловленности 45

11. Обусловленность задачи вычисления ОИ 45

12. Обусловленность задачи решения СЛАУ 46

Лекции 8-9-10-11. Методы интерполяции 50

13. Интерполяция обобщёнными многочленами 51

14. Кусочно-полиномиальная интерполяция 53

15. Оценка погрешности полиномиальной интерполяции 55

16. Интерполяция сплайнами 56

17. Интерполяционная формула Лагранжа для равноотстоящих узлов 62

Лекция 12. Вычисление определённых интегралов 66

18. Формула трапеции 67

19. Формула Симпсона 68

20. Формула Симпсона 3/8 69

21. Формула Буля 69

Список литературы 72

Лекции 1-2. Численные решения нелинейных уравнений

Постановка задачи на эту лекцию: решить уравнение , где , .

Напомним, что решить уравнение – это:

1. Установить, имеет это уравнение корни или нет

2. Если имеет, то сколько корней

3. И каковы их численные значения

Численное решение уравнения состоит из двух этапов:

1. Локализация корней

2. Итерационное уточнение корней

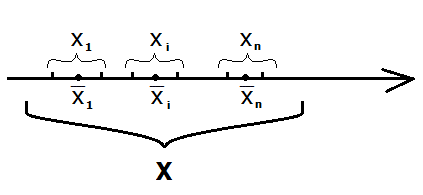
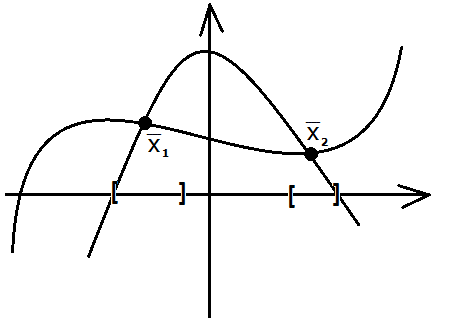
1.Локализация корней

Для того, чтобы осуществить локализацию корней, необходимо найти достаточно малые интервалы , такие что:

1. – они не пересекаются между собой;

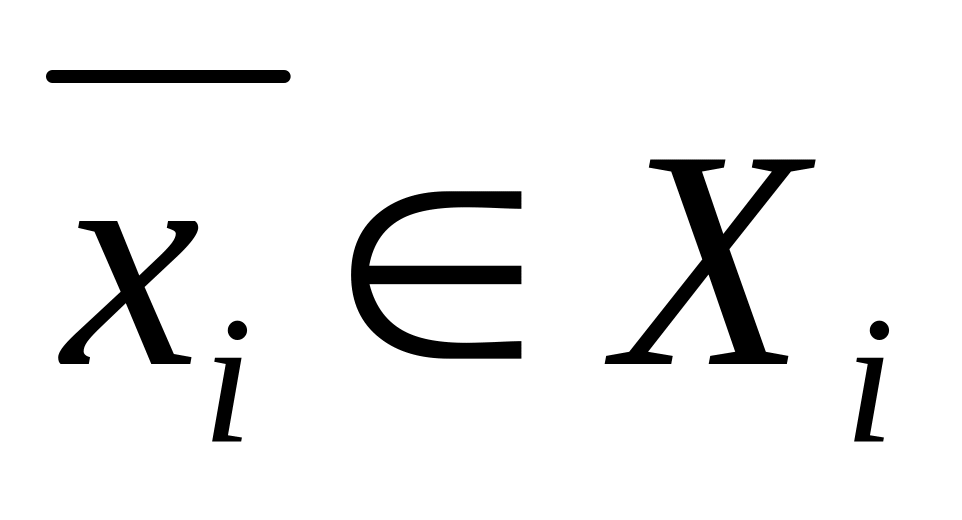2. – они содержат в себе корень исходного уравнения

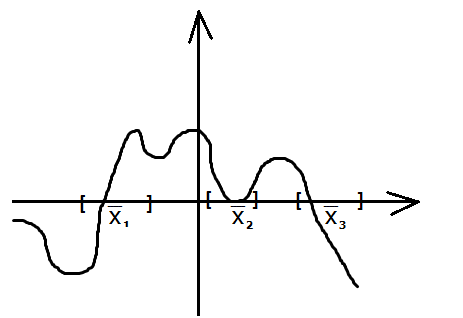
Часто локализацию корней можно выполнить визуально с помощью построения графика функции .

Если график построить сложно, то исходную функцию можно представить в виде разности двух функций , тогда исходное уравнение принимает вид:

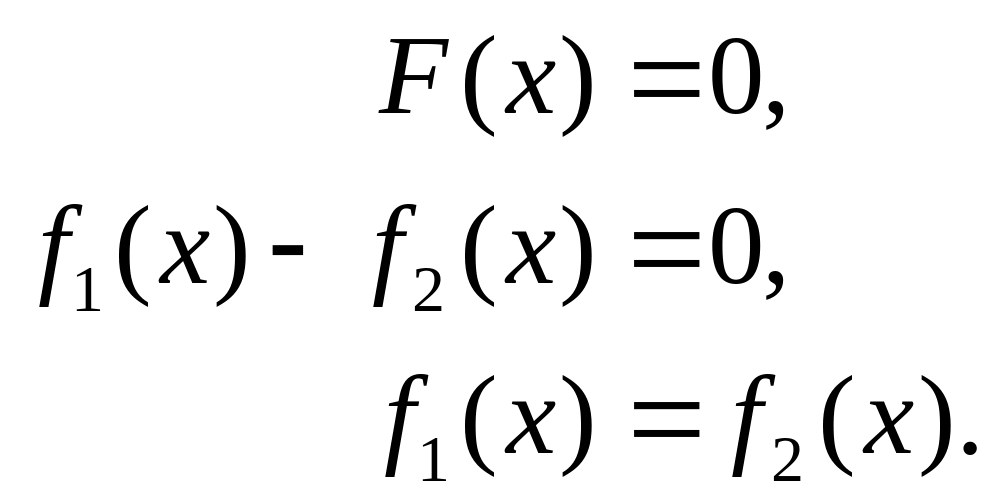
При этом корни определяются как точки пересечения графиков и :

Задача 1.1.

Осуществить локализацию корней следующего уравнения:

Решение. Введём две функции:

Далее необходимо визуально определить точки пересечения этих двух функций и записать интервалы, в которых они находятся. Точно вырисовывать графики на миллиметровой бумаге или с помощью компьютера вовсе не нужно. В данном случае достаточно понимания того, как ведут себя эти функции. Синус проходит через начало координат, далее при равен единице, а далее снова равен нулю при . Логарифмическая функция равна нулю при и единице при .

Следующий график, конечно, построен на компьютере, но на самом деле хватит всего вышеупомянутых точек, чтобы увидеть интервал локализации:

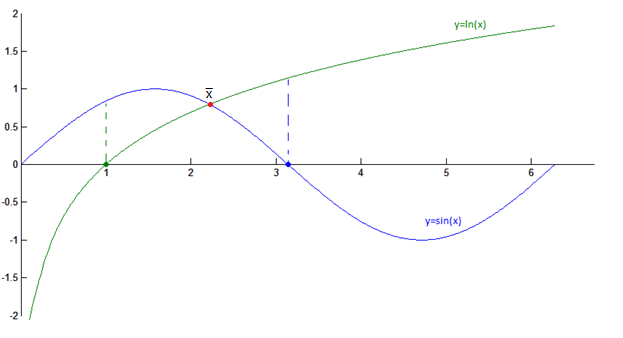
Ответ:

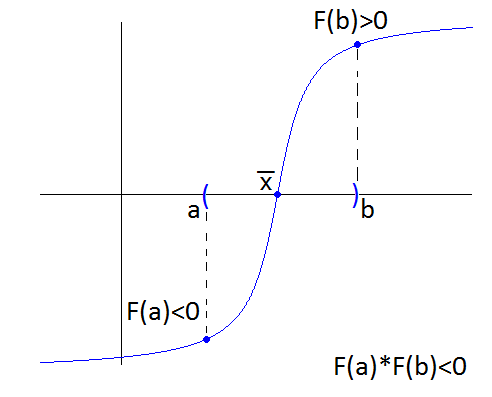
В более сложных и более сомнительных случаях локализацию корней для достоверности нужно подкрепить дополнительными вычислениями. При этом целесообразно использовать следующие достаточно очевидные положения:

1. Если функция которая непрерывна на отрезке , принимает на его концах значения разных знаков, то на интервале уравнение имеет по меньшей мере 1 корень:

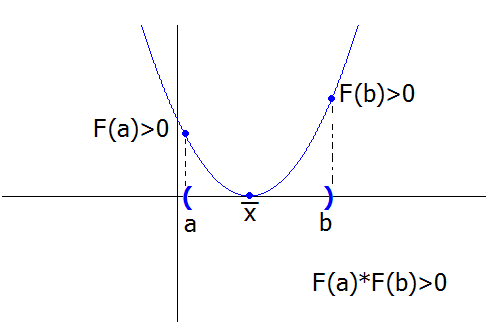
НО: Для корня кратной чётности это положение неприменимо, так как даже на малой окрестности функция знак не меняет:

2. Второе положение – следствие из первого. Если строго монотонна отрезке , а также если 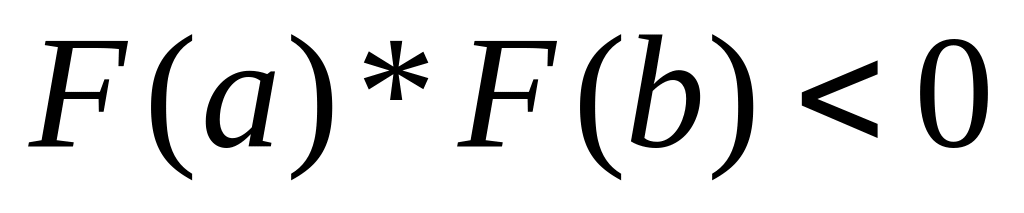(разные знаки на концах), то – единственный корень уравнения на данном отрезке.

Задача 1.2.

Локализовать корни уравнения .

Решение. Вначале упростим себе жизнь и разделим обе части уравнения на 4, затем, как и в предыдущем примере, разделимся на 2 функции:

Построим графики. Опять же, несмотря на то, что ниже приведён график, нарисованный компьютерной программой, нам она вовсе не требуется. Достаточно только понять, что график параболы проходит через точки , и , а график экспоненты в точке принимает значение , и левее этой точки асимптотически стремится к оси абсцисс. Начертив графики, проходящие через эти опорные точки, можно увидеть два наших корня:

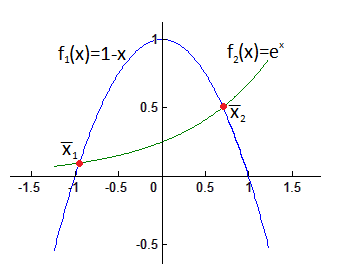
Ответ:

Осуществим проверку знакопеременности исходной функции на каждом из интервалов:

Для первого корня:

- левый край

- правый край

- условие выполнено

Для второго корня:

- левый край

- правый край

- условие выполнено

В особо сложных случаях, когда функция слишком сложна для построения, используют построение таблицы значений функции на исследуемом интервале.

Задача 1.3.

Локализовать корни уравнения на интервале .

Решение. Возьмём шаг и посчитаем значения функции от левой границы интервала до правой с этим шагом:

Видно, что функция меняет знак в трёх местах:

Значит корней всего три и мы их локализовали. Ответ: