3Передаточные функции системы
3.1 Разомкнутая и замкнутая передаточная функция
Для расчетов систем автоматического управления используются передаточные функции разомкнутой и замкнутой системы.
Передаточной функцией разомкнутой системы называется произведение всех передаточных функций последовательно соединенных звеньев прямого канала и канала обратной связи при размыкании системы в любом месте.
Передаточные функции замкнутой системы – это передаточные функции между выходной координатой и внешними воздействиями. Так как в заданной системе имеются два внешних воздействия (задающее воздействие и возмущающее – момент статический), следовательно, необходимо выводить две передаточные функции – по задающему и возмущающему воздействиям.
В общем случае передаточная функция замкнутой системы представляется в следующем виде:
(3.11)
где Wп, W0 - передаточные функции прямого канала и канала обратной связи для внешнего воздействия.
Из рисунка
2.7 в прямой канал по задающему воздействию
входят передаточные функции регулятора
Wрег,
тиристорного преобразователя
и двигателя
,
в канале обратной связи – передаточная
функция обратной связи по скорости Кс.
По формуле (3.1) передаточная функция
замкнутой системы по задающему воздействию
запишется:
(3.12)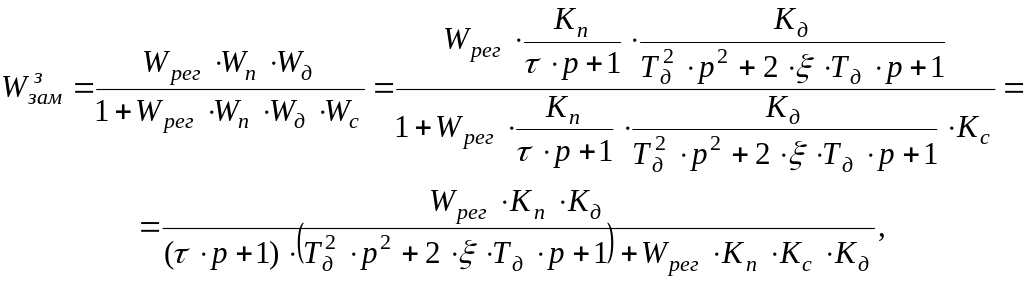
или
(3.13)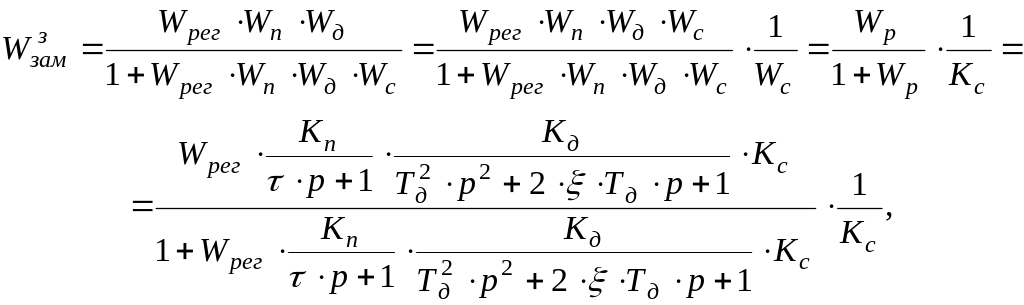
где 
- передаточная функция разомкнутой
системы:
(3.14)
Для возмущающего воздействия (момента) на основании рисунка 2.8а структурную схему можно представить как на рисунке 3.1.
При выводе передаточной функции по моменту необходимо встречно- параллельное соединение звеньев заменить на эквивалентную передаточную функцию по формуле (3.1) и учесть передаточную функцию Wм1.
Таким образом, передаточная функция замкнутой системы по моменту для схемы рисунка 2.8а выразится следующей формулой:
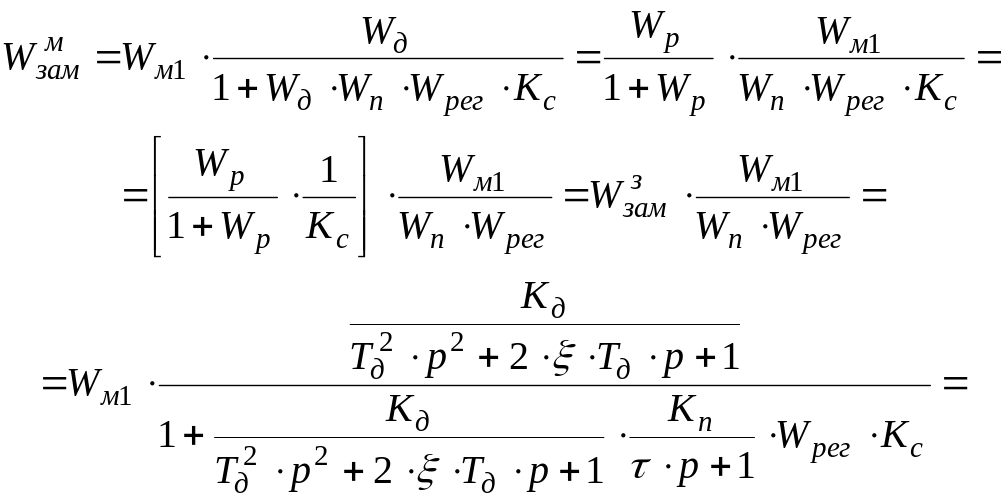
(3.15)
Для структурной схемы рисунка 2.8б передаточная функция замкнутой системы по моменту запишется так:
(3.16)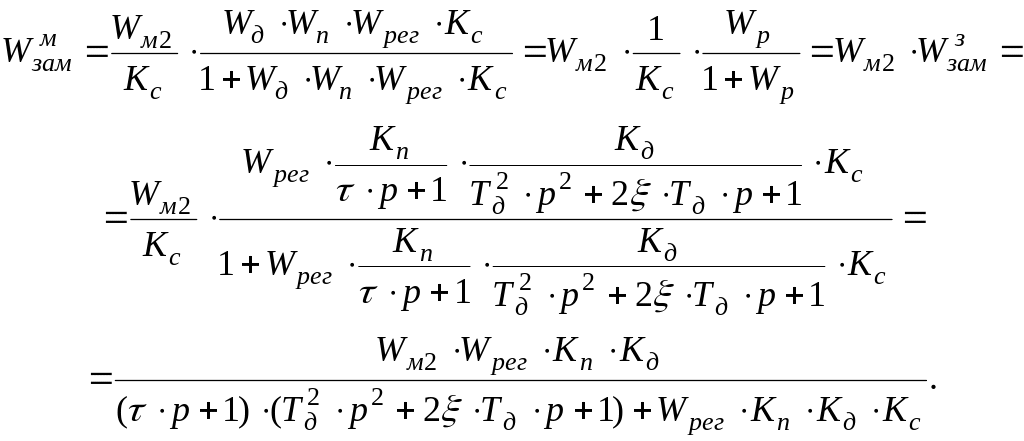
Нетрудно убедиться, что уравнения (3.5) и (3.6) абсолютно одинаковые, подстановкой в эти выражения передаточные функции Wм1 и Wм2.
3.2 Определение коэффициента усиления регулятора
В задании на
курсовую работу задано изменение
скорости при изменении момента от нуля
до номинального значения (ошибка
отклонения скорости в функции момента)
в процентах
.
Значение изменения скорости определяется по уравнению:
(3.17)
где εм% - заданная ошибка по моменту в процентах;
ωн - номинальная скорость, с-1.
Положив в формуле (3.5) оператор Лапласа равным нулю, определяется передаточная функция регулятора системы, которая записывается в виде:
(3.18)
Отсюда
коэффициент усиления регулятора:
(3.19)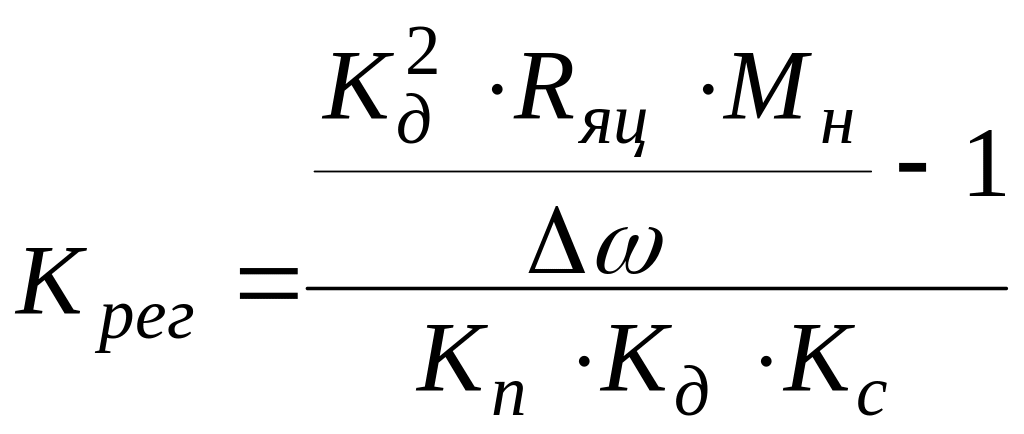
Полученное значение коэффициента усиления регулятора округляется до большего целого, для того чтобы точность была не хуже заданной.
При расчете устойчивости передаточную функцию регулятора предварительно представить в виде усилительного звена:
(3.20)
Если ошибка по моменту εм% равна 0, то коэффициент усиления регулятора по формуле (3.9) стремиться к бесконечности. В этом случае регулятор предварительно представить в виде интегрирующего звена с передаточной функцией:
(3.21)