Контрольные вопросы

8.1. Как определить оптимальные условия процесса?

8.2. Когда возникает необходимость в использовании метода Бокса-Вильсона? В чем он заключается?

8.3. Для чего ставится первая серия опытов полного факторного эксперимента при использовании метода Бокса-Вильсона?

8.4. Что такое экстремальный эксперимент?

8.5. Почему шаги при движении по градиенту должны быть кратны коэффициентам линейной модели?

8.6. Как рассчитываются шаги в изменении факторов при крутом восхождении?

8.7. Как оценивают эффективность движения по градиенту?

8.8. Как правильно выбрать интервал варьирования при движении по градиенту?

8.9. При движении по градиенту значение одного из факторов выходит за пределы опытов. Как поступать в таких случаях?

8.10. Что такое градиент функции? Какова его геометрическая интерпретация?

8.11. В чем преимущества метода поиска оптимума по алгоритму Бокса-Вильсона перед обычным однофакторным?

Краткие ответы

8.1. Поиск оптимальных условий является одной из наиболее распространенных научно-технических задач. Они возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие (оптимальные в некотором смысле) условия его реализации. Например, требуется так подобрать концентрации реагирующих веществ, температуру, давление, время реакции и другие факторы, чтобы сделать выход продукта возможно более близким к 100 %. Но это далеко не единственно возможная постановка задачи. Найденные условия оказались бы другими, если бы ставилась, например, цель минимизации количества вредных примесей.

8.2. При исследовании поверхности отклика с целью нахождения экстремума удобно воспользоваться методом Бокса-Вильсона.

Исследователь, определяя оптимум по данной методике, должен выполнить действия в следующем порядке:

1. Наметить и реализовать первую серию экспериментов типа 2^k.

2. По результатам этой серии рассчитать линейные эффекты.

3. Оценить градиент регрессионной модели.

4. В направлении градиента наметить еще несколько опытов.

5. Когда в направлении градиента достигается область экстремума, при необходимости планируется завершающая серия опытов с целью построения квадратичной полиномиальной модели.

8.3. Предполагается, что эксперимент ставиться с точки, достаточно удаленной от оптимума; поэтому для описания поверхности отклика в окрестности начальной точки можно использовать линейную модель.

После реализации первого этапа линейные эффекты рассчитываются по формуле

(i=1, 2, …, k).

Найденные коэффициенты будут указывать направление градиента.

8.4. Эксперимент, который ставится для решения задач оптимизации, называется экстремальным. Это название связано с глубокой аналогией между оптимизацией и поиском экстремума некоторой функции. Задача является экстремальной, если цель ее состоит в поиске экстремума некоторой функции.

8.5. В результате факторного эксперимента получают уравнение регрессии, описывающее функцию отклика в некоторой ограниченной области факторного пространства. Если данная модель адекватна, то ее используют для выбора направления движения к области оптимума. В полученной модели коэффициенты регрессии представляют собой частные производные функции отклика по соответствующим факторам. Поэтому, если i, j, ..., z - единичные векторы в направлении координатных осей, то градиент

grad y =

задает кратчайшее направление движения к экстремуму. Очевидно, что для осуществления такого движения необходимо изменять факторы пропорционально соответствующим коэффициентам регрессии.

Из аналитической геометрии известно, что первая производная в геометрической интерпретации представляет собой угол наклона каса­тельной к кривой. Используя рис. 8.1, можно записать:

d₃

y΄ y

d₂

d₁

d

θ c c₁ c₂ c₃

y₀΄

-1 0 1 2 3 4 x_i΄

Δx_i

Рис. 8.1. График движения по градиенту

п ри одном факторе

x0 x_i΄

Значение функции в точках, лежащих на градиенте, можно опре­делить по выражению

y = y₀΄ + 0c tg θ,

где 0с = Δx_i - интервал варьирования фактора. Следовательно,

y = y₀΄ + Δx_i tg θ,

8.6. Шаги при движении по градиенту рассчитывают в натуральном масштабе. Для этого вначале определяют произведения коэффициентов на соответствующие интервалы варьирования (b_i·Δх_i), а затем рас­считывают шаги в изменении каждого фактора пропорционально этим произведениям. При этом шаги можно округлять, а умножение состав­ляющих градиента на любое число также дает точки, лежащие на градиенте.

В зависимости от того, что желают найти, максимум или мини­мум, полученные таким образом шаги последовательно прибавляют или вычитают из основного уровня каждого фактора. Знаки коэффициентов необходимо учитывать. Подобным образом намечают серию экспери­ментов движения по линии градиента. Эти опыты иногда называют мысленными, поскольку не все они должны быть реализованы.

8.7. Движение по градиенту в каждом конкретном случае (рис. 8.1) представляет собой шаговую операцию, которая продолжается до тех пор, пока не будут получаться результаты ниже предыдущих. Значение отклика при значениях х, равных с, c₁ , с₂, ... , будут меньше предсказан­ных линейной моделью, однако cd < c₁d₁ < c₂d₂ < c₃d₃. В точке x_i = с₃ ре­зультат опыта окажется не только меньше предсказываемой величины c₃d₃, но и меньше предыдущего значения c₂d₂. В этом случае движение по градиенту прекращается. Вблизи точки x_i = c₂ ставится новая серия опытов с целью описания функции отклика в окрестностях оптимума или отыскания нового направления движения к оптимуму.

Экстремум считается достигнутым, когда при движении по линии градиента достигается «перевал», т.е. монотонно возрастающие отклики сменяются на противоположное направление, или наоборот.

8.8. Для фактора с наибольшим произведением (b_iΔx_i) выбирается шаг для движения по градиенту. Шаги всех остальных факторов полу­чают, умножая величину выбранного шага на коэффициент пропорцио­нальности К. Выбор интервала варьирования при движении по градиен­ту всецело зависит от интуиции исследователя. Никаких строгих правил, определяющих эту процедуру, нет. Можно только рекомендовать выби­рать интервал таким образом, чтобы при первом движении оказаться ли­бо вблизи границы исследования, либо несколько выйти за ее пределы. Если при этом окажется, что существующее оборудование не может обеспечить четкого задания значений по некоторым факторам из-за ма­лости получившихся интервалов, то их следует менять через два-три опыта. Для удобства интервалы можно округлить.

8.9. При движении по градиенту часто встречается ситуация, при которой движение по одному из факторов достигает некоторого предела. В таких случаях этот фактор стабилизируют и продолжают движение по оставшимся.

8.10. Вектор-градиент непрерывной функции у = φ(х₁, х₂, ... х_n) имеет вид

grad y = .

Этот вектор перпендикулярен поверхности равного уровня у = const и указывает направление наискорейшего подъема (крутого восхождения).

8.11. На графиках поиска оптимума методом движения с помо­щью одно факторного эксперимента и по градиенту (рис. 8.2) показаны кривые равного значения отклика, спроектированные на плоскость x₁0x₂. Экспериментатор находится в точке О. Локальное описание поверхности отклика в окрестностях точки О дает исследователю возможность вы­брать направление, которое совпадет с градиентом, и двигаться по этому направлению до точки С. Дальнейшее движение приведет к снижению выхода.

В точке С ставится серия опытов, по которой выбирается новое направление движения к оптимуму. Можно показать, что путь к опти­муму по прямой ОС является кратчайшим. Для этого на рис. 8.2 приведе­ны два варианта движения традиционным методом, при котором движе­ние к оптимуму осуществляется методом однофакторного эксперимента. При этом методе экспериментатор стабилизирует один фактор на неко­тором уровне и варьирует другим. Из двух путей ОАВ и ОДЕ (рис. 8.2) рассмотрим один - ОАВ. Зафиксировав х₂ на некотором постоянном уровне, исследователь движется в направлении x₁ до точки А, так как дальнейшее движение в этом направлении приводит к снижению выхо­да. В точке А фиксируется переменная x₁ и начинается движение по х₂, оно происходит до точки В, т.е. до тех пор, пока наблюдается прирост выхода. В этой точке фиксируется х₂ и снова происходит движение по x₁.

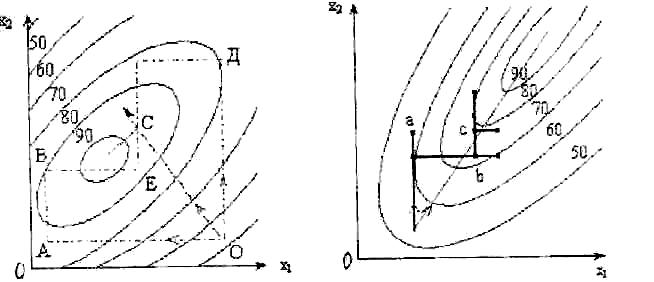
Рис. 8.2. Схема поиска оптимума Рис. 8.3 Схема поиска оптимума

Функции с помощью однофакторного функции, имеющей вид гребня

эксперимента и методом движения

по градиенту

34