Контрольные вопросы

5.1. Почему нельзя рассчитать квадратичные эффекты воспользовавшись столбцом аналогично тому, как определяется коэффициент b₁₂ по столбцу x₁•x₂?

5.2. Что такое «звездное плечо»?

5.3. Есть ли разница в методах расчета коэффициентов в уравнениях регрессии первого и второго порядка?

5.4. Как проверить адекватность уравнения второго порядка?

5.5. Как рассчитать число коэффициентов в полиноме второго порядка?

5.6. Почему для нахождения коэффициентов нельзя воспользоваться полным факторным экспериментом типа 3^к?

5.7. Чем отличаются планы второго порядка друг от друга?

5.8. Как проверить значимость коэффициентов в уравнении регрессии второго порядка?

5.9. Как построить композиционный план второго порядка?

5.10. Для чего в ортогональных планах второго порядка преобразуется столбец квадратичных эффектов?

5.11. Почему в расчетах планов второго порядка дважды встречается свободный коэффициент – b₀ b₀'?

5.12. Какие планы можно реализовать для изучения поверхности отклика?

Краткие ответы

5.1 Модель первого порядка включает только линейные эффекты и эффекты взаимодействия. Между тем существенными могут оказаться коэффициенты при квадратах факторов, их кубах и т. п.

Попытка построения вектор-столбцов для х₁² и х₂² приводит к получению единичных столбцов, совпадающих друг с другом и со столбцом x₀. Так как эти столбцы неразличимы, то нельзя сказать, за счет чего получилась величина b₀: она включает значение свободного члена и вклады квадратичных членов. Имеет место смешанная оценка:

5.2.Добавляемые к плану линейной модели точки, расположенные на расстоянии от центра, называют «звездными», а само расстояние от центра плана до звездной точки - «звездным плечом». Выбором величины плеча а композиционного плана и числа точек n в центре могут быть обеспечены различные свойства получаемого плана.

Плечо можно выбрать таким образом, чтобы план оставался ортогональным, т.е. чтобы скалярные произведения всех векторов-столбцов в матрице независимых переменных были равны нулю. Можно выбрать плечо а таким образом, чтобы удовлетворить критерий ротатабельности, т.е. добиться такого положения, при котором дисперсии предсказанного значения отклика были одинаковы на равных расстояниях от центра плана.

Композиционные планы приводятся к ортогональным выбором соответствующего звездного плеча. Значения ² в зависимости от числа дублей в центре плана и числа факторов приведены в табл. 5.1.

Таблица 5.1. Значения ² для различного числа факторов и количества опытов в центре плана

Число факторов	Число опытов в центре плана
	1	2	3	4	5	6	7
2	1,000	1,160	1,317	1,475	1,606	1,742	1,873
3	1,476	1,650	1,831	2,000	2,164	2,325	2,481
4	2,000	2,164	2,390	2,580	2,777	2,.950	3,140

5.3. В композиционных ортогональных планах второго порядка все коэффициенты уравнения регрессии определяют независимо друг от друга:

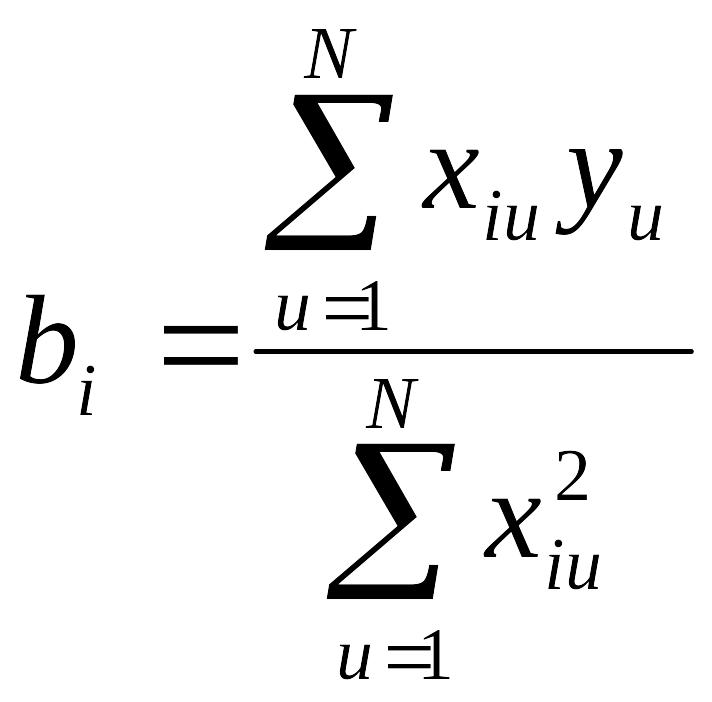
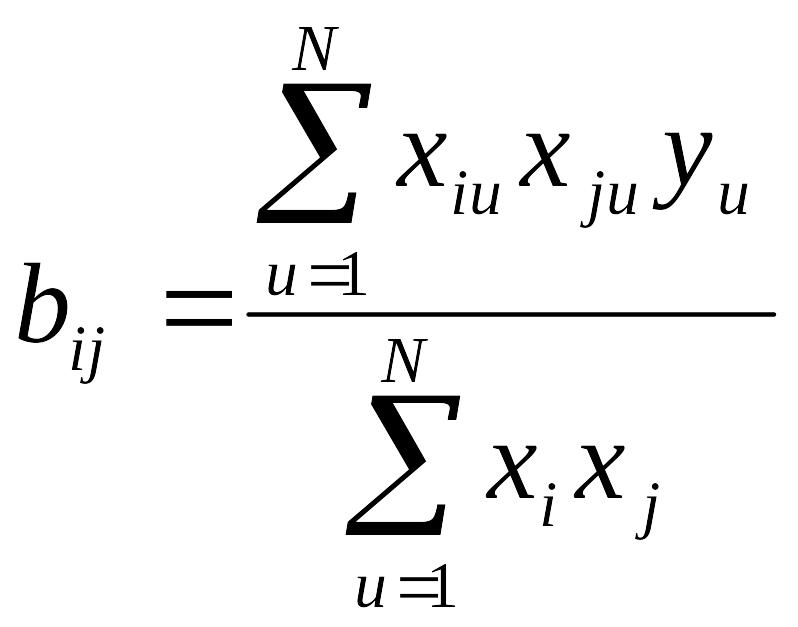
В отличие от линейных, в ортогональных планах второго порядка дисперсии коэффициентов не равны между собой, т.е. коэффициенты рассчитывают с разной точностью:

Знаменатель в этих формулах ( ) не зависит от результатов опытов, поэтому его можно вычислить заранее, что упрощает обработку результатов эксперимента.

5.4 Адекватность проверяют по критерию Фишера, составляя отношение дисперсий: Fрасч = /

Уравнение адекватно, если составленное таким образом F-отношение меньше табличного для выбранного уровня значимости и чисел степеней свободы дисперсии адекватности и дисперсии воспроизводимости:

где f_ад = N-L - число степеней свободы дисперсии адекватности, N -число опытов в матрице планирования; L - число значимых коэффициентов в уравнении регрессии;

f_y = n-1 - число степеней свободы дисперсии воспроизводимости; n - число дублей.

5.5 Планы второго порядка содержат, кроме основных эффектов, все парные взаимодействия и квадратичные эффекты. Число коэффициентов в полиноме второго порядка

L = (k+ l)•(k + 2)/2.

5.6 Трехуровневый план, в котором реализованы все возможные комбинации из к факторов на трех уровнях требуют слишком большого числа опытов, намного превышающего число определяемых коэффициентов уже при числе факторов больше 2:

Число:

факторов k 2 3 4 5

опытов в ПФЭ 9 27 81 243

определяемых коэффициентов L 6 10 15 21

Можно сократить число опытов, воспользовавшись композиционными планами.

5.7 Планы полного факторного эксперимента типа З^к неприемлемы из-за большого количества опытов. Попытка сократить число опытов, необходимых для нахождения всех коэффициентов регрессии второго порядка, привела к разработке различных планов. Однако, в отличие от планов первого порядка, построение планов второго порядка, отвечающих одновременно многим критериям оптимальности, оказалось невозможным. Предложено большое количество планов второго порядка, удовлетворяющих отдельным критериям оптимальности.

По методу построения планы второго порядка бывают композиционные и некомпозиционные.

В зависимости от того, какие точки добавляются к планам первого порядка, композиционные планы могут быть центральные и нецентральные. Математическая теория планирования эксперимента наиболее полно разработана для центральных композиционных ортогональных и центральных композиционных ротатабельных планов.

Для определения значимости коэффициентов необходимо по опытам в центре плана определить дисперсию воспроизводимости . В отличие от планов первого порядка величина для каждого коэффициента рассчитывается индивидуально (см. ответ 5.3).

Значимость коэффициентов проверяется по критерию Стъюдента:

Коэффициент значим, если t^расч больше t^табл с соответствующим уровнем значимости и числом степеней свободы, равным числу продублированных опытов минус единица.

5.9 Композиционный план для квадратичных моделей может быть получен путём добавления некоторого количества специальных точек к «ядру». В качестве «ядра» могут быть использованы планы типа 2^k или 2^k-р. К ядру добавляются точки в центре плана с координатами 0, …,0 и так называемые «звездные» точки. На рис. 5.1 показаны схемы композиционных планов для двухфакторного и трехфакторного экспериментов. Здесь в качестве ядра использованы точки полного факторного эксперимента (обозначены кружками). Крестиками обозначены звездные точки, расположенные на координатных осях на расстоянии от центра плана.

x₂

3

4

1

2

7

8

6

x₁

x₁

3

5

4

2

1

x₂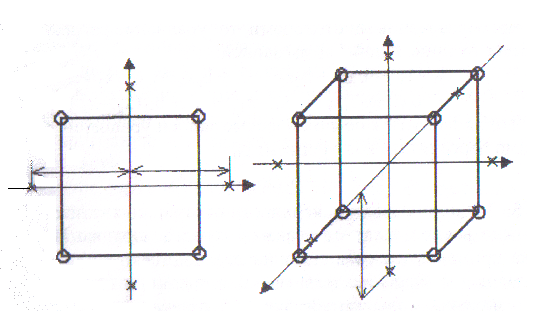

Рис. 5.1. Композиционные планы второго порядка: а - для k=2; б - для k=3

Матрица планирования композиционного плана второго порядка для двух факторов, соответствующая рис. 5.1, представлена в табл. 5.2.

Таблица 5.2. Композиционный план второго порядка для двух факторов

Опыты	Номер опы­та	Код опыта	x0	x1	x2
На ядре плана	1	ab	+1	+1	+ 1
	2	а	+1	+1	-1
	3	b	+1	-1	+ 1
	4	-1	+1	-1	-1
В звездных точках	5	+ (а)	+1	+	0
	6	- (а)	+1	-	0
	7	+ (b)	+1	0	+
	8	- (b)	+1	0	-
В центре плана	9	0	+1	0	0
	…	0	…	…	…
	N	0	+1	0	0

5.10. Для получения ортогональной матрицы необходимо, выбрав звездное плечо, преобразовать квадратичные столбцы

.

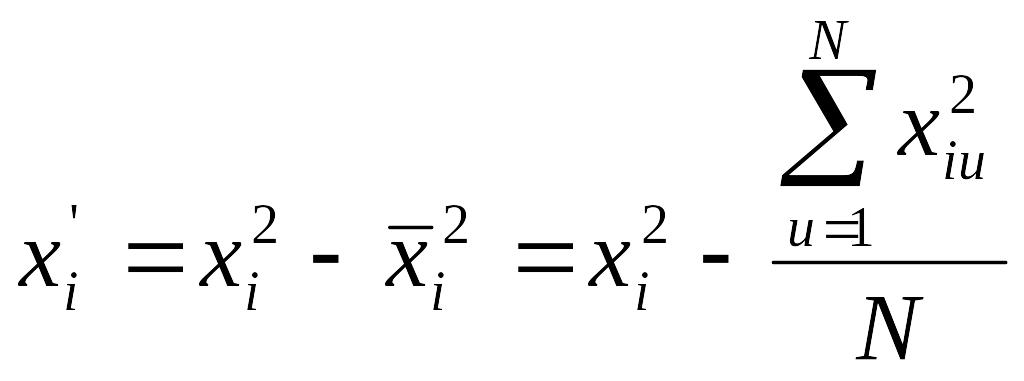5.11 Так как расчеты для квадратичных эффектов ведутся по мат­рице с преобразованными столбцами, то уравнение регрессии несколько отличается от привычной формы записи:

Чтобы перейти к обычной форме записи уравнения регрессии, необходимо пересчитать коэффициент b₀:

b₀ = b₀'-b₁₁

5.12 Для описания поверхности отклика со значительной кривизной можно воспользоваться планами второго порядка. Планы третьего порядка применяются сравнительно редко, только в тех случаях, когда квадратичная модель неадекватна. Для оценки коэффициентов модели второго порядка, содержащей функции независимых переменных типа , эта переменная (x) в плане должна принимать, по крайней мере, три различных значения. Если априорная информация об объекте исследования отсутствует и полиоминальную модель приходится подбирать последовательно, начиная с линейной модели, то целесообразно воспользоваться композиционными планами, содержащими в «ядре» планы первого порядка.