Контрольные вопросы

4.1. Как рассчитать коэффициенты, если опыты дублируются?

4.2. Для чего опыты необходимо повторять несколько раз?

4.3. Как сравнить дисперсии между собой?

4.4. В каком случае рассчитанный коэффициент считается статистически значимым?

4.5. Что такое остаточная дисперсия?

4.6. Что такое стандартное отклонение?

4.7. Как проверить адекватность уравнения эксперименту?

4.8. Для чего необходимо знать дисперсию опытов?

4.9. Как рассчитать дисперсию опытов?

Краткие ответы

4.1. Статистическую обработку результатов полного факторного эксперимента, при дублировании измерений, желательно начать с рассмотрения однородности дисперсий и отброса грубых измерений. Если дублируются текущие измерения, то после отброса грубых измерений в каждой строке плана эксперимента рассчитывается среднее, и по ним оцениваются коэффициенты, если ставятся дубли в центре плана, то расчет коэффициентов ведется по единичным измерениям. В общем виде формула для оценки эффектов имеет вид

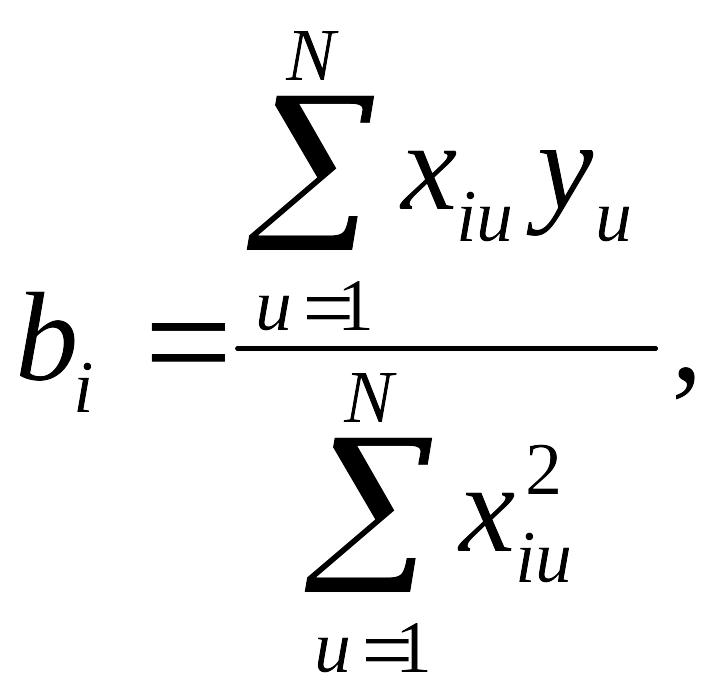
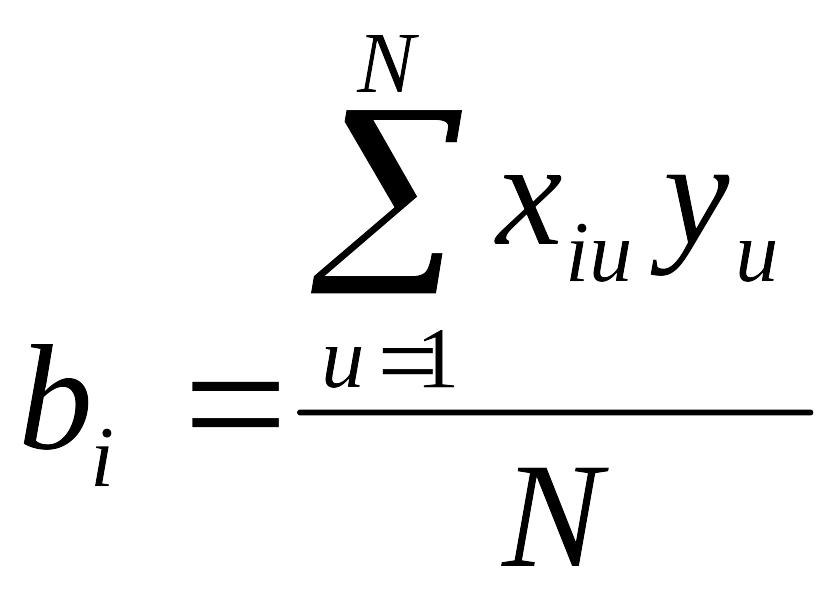
(i=0,1,…,k),

здесь i - номер фактора; u - номер опыта.

4.2. По параллельным опытам оценивается ошибка опыта (ошибка воспроизводимости). Для этого опыт воспроизводится в одинаковых условиях несколько раз и затем берется среднее арифметическое всех результатов - у:

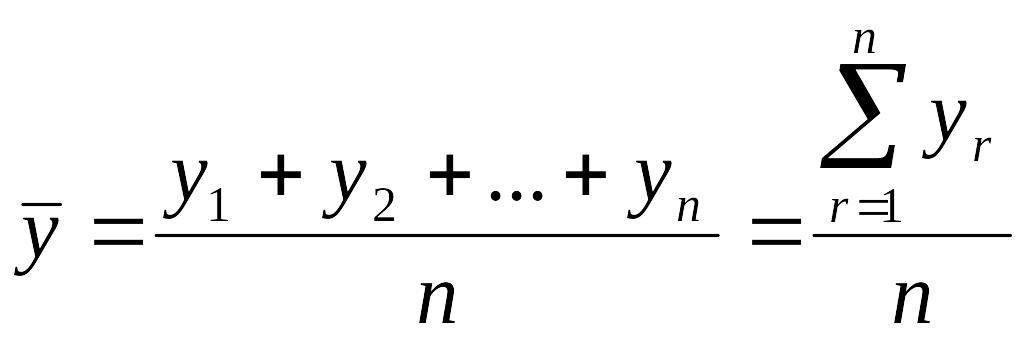
Далее рассчитывается дисперсия , характеризующая рассеяние результатов экспериментов и стандартное отклонение (см. ответ 4.8). Результат опыта может быть представлен в виде

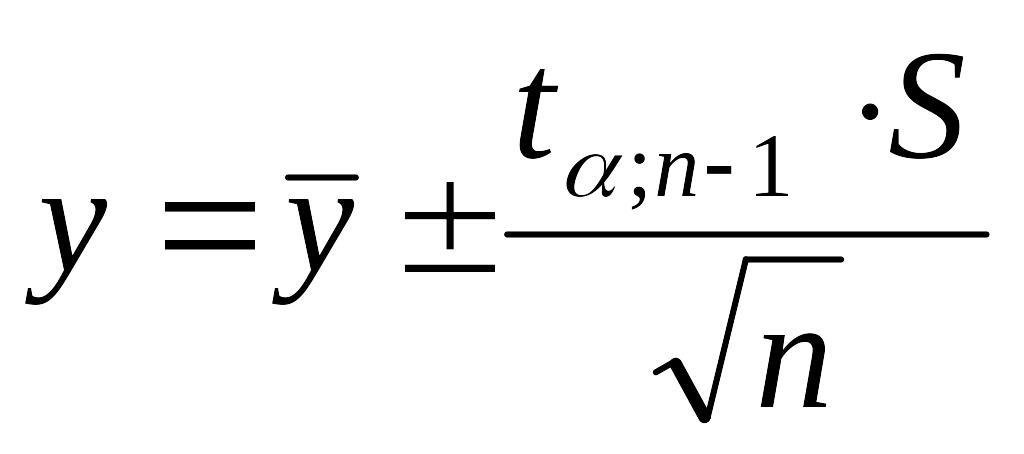
4.3 Оценить однородность можно по критерию Фишера. Критерий Фишера (F-критерий) представляет собою отношение большей дис­персии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия. Если полученное значение дисперсионного отношения больше приведенного в таблице для соответствующих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т.е. что они неоднородны.

4.4 Проверку значимости коэффициентов можно осуществить двумя способами. В одном случае можно сравнивать абсолютную величину коэффициента с его доверительным интервалом, рассчитываемым по формуле

где - критерий Стьюдента, берется из таблиц, в зависимости от числа степеней свободы при определении дисперсии опыта и выбранно­го экспериментатором уровня значимости .

Коэффициент считается статистически значимым, когда его абсолютная величина больше доверительного интервала, т.е.

или

Смысл этого неравенства заключается в том, что абсолютная величина коэффициента должна быть в t раз больше, чем ошибка определения.

В другом случае можно получить расчетное значение t-критерия и сравнить его с табличным:

,

Коэффициент значим, если расчетное значение критерия Стьюдента больше табличного:

Статистическая незначимость коэффициентов интерпретируется как отсутствие влияния соответствующего фактора (или взаимодействия факторов) в изученных интервалах его изменения. Эти коэффициенты из уравнения регрессии могут быть исключены.

4.5. Остаточная дисперсия, или дисперсия адекватности эксперимента рассчитывается по формуле

где и соответственно, экспериментальное и расчетное значения отклика в u-м опыте; -число степеней свободы дисперсии адекватности, равное разности между числом опытов в плане эксперимента N и числом значимых коэффициентов L в уравнении регрессии, включая N-L.

4.6 Корень квадратный из дисперсии, взятый с положительным знаком, называется средним квадратичным отклонением, стандартом, стандартным отклонением, или квадратичной ошибкой S. Среднеквадратичная ошибка в определении коэффициентов

4.7 Гипотезу об адекватности, чаще всего проверяют с помощью критерия Фишера - F. Уравнение адекватно описывает эксперимент, если расчетное значение F-критерия не превышает табличного для выбранного уровня значимости, т.е. когда выполняется соотношение

Расчетное значения критерия Фишера - это отношение остаточной дисперсии (дисперсии адекватности) к дисперсии опыта:

4.8. Отклонение результата любого опыта от среднего арифметического можно представить как разность , где - результат отдельного опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений повторных опытов. Для измерения этой изменчивости чаще всего используют дисперсию. Дисперсией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозначается .

При дублировании только одного опыта (чаще на основном уровне) оценку дисперсии воспроизводимости опытов получают по формуле

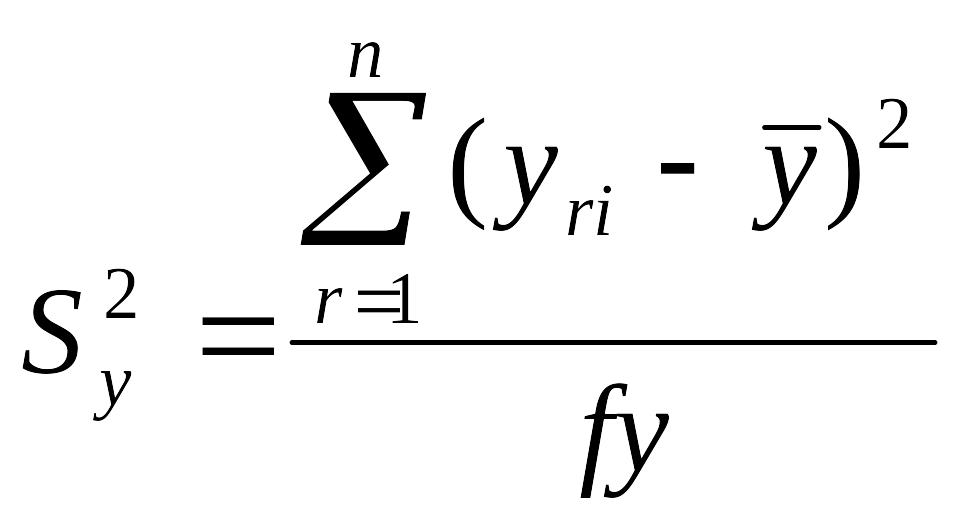
где г - номер параллельного опыта; n - число параллельных опытов; у - среднее арифметическое всех параллельных опытов; - число степеней свободы, = n - 1, равное количеству опытов минус единица. Одна степень свободы использована для вычисления среднего значения.

Матрица планирования состоит из серии опытов, и дисперсия все­го эксперимента получается в результате усреднения дисперсий всех опытов. Дисперсию параметра оптимизации (суммарную дисперсию воспроизводимости) можно рассчитать по формуле

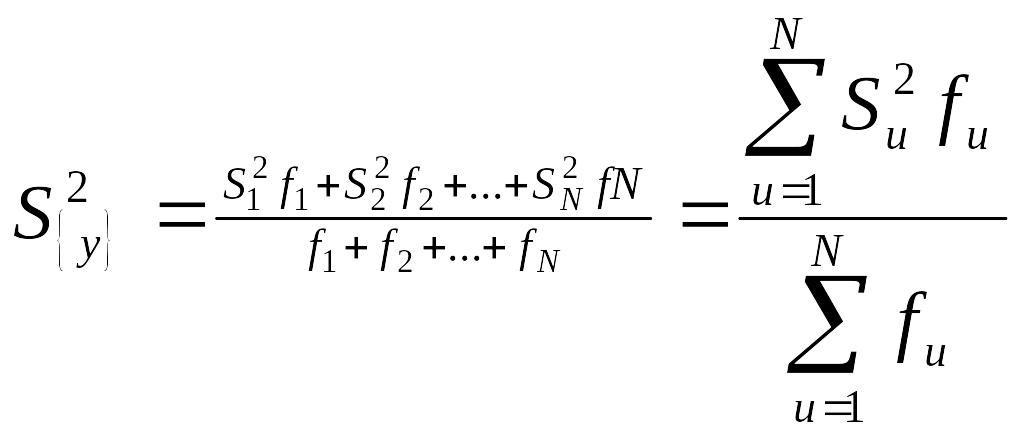
Пользоваться ею можно в тех случаях, когда дисперсии однородны. Последнее означает, что среди всех суммируемых дисперсий нет таких, которые бы значительно превышали все остальные. Проверка однородности дисперсий может быть произведена с помощью критерия Фишера (см. ответ 4.3).