§6.Бесконечные пределы

Определение. Расширенной прямой будем называть множество с естественным продолжением основных операций из , а именно:

1. 

2. ;

3. не определено; ;

4. ; ; и не определены

5. 

6. не определено; .

Замечание1. Операции «-» и «/» получаются из «+» и « » переходом к обратным.

Замечание2. Для «+» и « » коммутативность, ассоциативность и дистрибутивность сохраняются в .

Определение1. , если .

Определение2. , если .

Замечание1. Если имеет бесконечный предел, то не ограничена, кроме того, обратное неверно.

Замечание2. Естественным образом можно определить и для , так как — верхняя грань ; — нижняя грань .

Замечание3. ;

Замечание4. и .

Замечание5. Критерий о том, что

верен в .

Теорема. Свойства пределов, связанные с арифметическими операциями, остаются верными в , когда эти операции определены. Доказательство:

1. .

2. .

3. . .

Замечание. Случаи и в пунктах II. и III. получаются из описанных случаев домножением соответствующих последовательностей на -1.

§7. Аксиома отделимости. Некоторые функции

Аксиома(верхней грани). Пусть и . Тогда .

Теорема. Аксиома отделимости Аксиома верхней грани. Доказательство: . Возьмем (он существует, так как — верхняя грань ). Такое подходит. Действительно, , так как — верхняя грань , так как — наименьшая из верхних граней.

. Пусть и у есть верхняя грань. Обозначим — множество всех верхних граней множества . Заметим, что . Тогда по аксиоме отделимости . Значит, — верхняя грань множества и наименьшая из всех верхних граней. Тогда . Теорема доказана.

Некоторые функции

1. Будем последовательно определять эту функцию на различных подмножествах :

   1. : ;

   2. ;

   3. ;

   4. :

, то есть такое число , что . Докажем, что такое существует. Пусть — множество чисел , — множество чисел . Очевидно, что . Тогда по аксиоме отделимости . Теперь докажем, что . Будем строить доказательство от противного. Пусть . Рассмотрим . Если такое существует, то , что противоречит выбору . Докажем, что такое существует. , где — некоторая константа, полученное с помощью замены по неравенству , . Пусть . Рассмотрим такие числа: — множество, полученное из заменой всех элементов на обратные им ( определяется аналогично). Тогда и . Как было доказано ранее, такого случая не бывает. Доказательство окончено. Для необходимо взять .

5. :

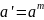Введем некоторые множества: , , , . Предположим, что , иначе заменим на . Тогда . Тогда по аксиоме отделимости . Обозначим . Докажем, что такое единственно. Рассмотрим , кроме того . Такие последовательности, очевидно, существуют, так как на любом интервале найдется рациональное число. Теперь докажем, что , что равносильно тому, что . Заметим, что . Но , где — некоторая натуральная константа, . Тогда .