Графики изменения нагрузки и перегревов проводника

2.3. Электрическая аналогия тепловых процессов и понятие о тепловых сопротивлениях

Однородное тело, которое мы рассматривали в § 2.1, имеет два тепловых свойства - при поступлении в него энергии оно, во-первых, накапливает энергию в себе, повышая свою температуру, а во-вторых – отдает часть

полученной энергии в охлаждающую среду. Нет ли сочетания аналогичных свойств у электрических аппаратов, частей электрической цепи?

Что накапливает энергию в электрической цепи и за счет этого повышает свой (присущий ему) энергетический показатель? Это – электроемкость. Она получает электрический заряд q и вследствие этого повышает разность потенциалов на своих обкладках . Как известно, потенциал – энергетический показатель электрической цепи. Размерность электрической емкости

[C] = Кулон/Вольт = Фарада.

Этому параметру полностью идентичен тепловой параметр – теплоемкость C, размерность которой

[C] = Джоуль/градус,

причем градус (точнее – температура) - именно присущий процессу нагрева энергетический показатель.

По участку электрической цепи протекает электрический ток I, вызываемый разностью потенциалов ₂ - ₁ и ограничиваемый величиной электрического сопротивления R.

Но и при нагреве однородного тела можно найти процесс, в той или иной степени аналогичный электрическому току. Это – процесс отдачи тепла от тела к охлаждающей среде с коэффициентом теплоотдачи A, то

есть тепловой поток, вызываемый разностью температур

тела _т и охлаждающей среды _ос.

Электрическое сопротивление R находится в знаменателе закона Ома, и с ростом сопротивления ток уменьшается. Коэффициент теплоотдачи A является сомножителем во втором слагаемом выражения (2-6), то есть в рассматриваемой аналогии A является тепловой проводимостью.

По аналогии с выражением Закона Ома для элект-рической цепи

₂ - ₁

I = ------------ (2-22)

R

можно написать такое же выражение и для тепловых цепей

₂ - ₁

Q = ------------ = (₂ - ₁) A, (2-23)

R_т

где Q - тепловой поток в Ваттах, а ₂, ₁ - температуры в градусах начала и конца участка тепловой цепи, т. е. тела

(₂=_т) и охлаждающей среды (₁=_ос);

R_т - тепловое сопротивление участка цепи между точ-ками 1 и 2, градус/Ватт.

В случае однородной плоской стенки тепловой поток через единицу поверхности этой стенки определяется законом Фурье – основным законом теплопроводности

q = (₂ - ₁)/ =  /, (2-24)

где  - разность температур на поверхностях стенки;

 - толщина стенки;

 - коэффициент теплопроводности, Вт/(м град).

Если перейти к тепловому потоку через какое-то сечение S

Q = q S = S  / = /R_т, (2-25)

где R_т - тепловое сопротивление стенки, то есть участка тепловой цепи длиной  и сечением S



R_т = ----------. (2-26)

S 

Очевидна аналогия с электрическим сопротивлением



R = ---------. (2-27)

S γ

Отсюда видно, что коэффициент теплопроводности 

аналогичен удельной электрической проводимости γ. Его

величина для материалов, широко применяющихся в

электроаппаратах, составляет в Вт/(м градус)

- обмоточная отожженная медь . . . . . . . . . . . . .. . . . . . .350

- проводниковый алюминий . . . . . . . . . . . . . . . . . . . . . 250

- электротехническая холоднокатаная сталь

с лаковой изоляцией вдоль направления проката . . . . 21

- то же, поперек направления проката . . . . . . . . . . . . . . 1,2

- конструкционная сталь . . . . . . . . . . . . . . . . . . . . . . . . . .50

- вода при отсутствии циркуляции . . . . . . . . . . . . . . . . 0,56

- трансформаторное масло при

отсутствии циркуляции . . . . . . . . . . . . . . . . . . . . . . . 0,15

- резина . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,22

- электрокартон, пропитанный маслом . . . . . . . . . . . . 0,25

- воздух при температуре 20^оС, нормальном

давлении и отсутствии циркуляции. . . . . . . . . . . . . .0,022

Таким образом, воздух при отсутствии циркуляции является самым плохим проводником тепла и, наоборот,

одним из самых хороших теплоизоляционных материалов. Следующий плохой проводник – нециркулирующее трансформаторное масло. При наличии циркуляции – движении масс воздуха или масла – соответствующие значения  увеличиваются в несколько раз.

Хорошие проводники тока являются и хорошими проводниками тепла, а электроизоляторы являются

теплоизоляторами, поэтому, например, обмотка, выполненная из меди или алюминия, и заключенная в изоляцию, будет иметь плохой теплоотвод.

Если заданы температуры, то по выражению (2-23) можно рассчитать тепловой поток только при ₁ = Сonst,

и при ₂ = _у, то есть при отсутствии накопления энергии за счет теплоемкости. В общем случае уравнению (2-6) соответствует схема замещения с теплоемкостью C и

сопротивлением R_т.

Задачи теплового расчета электроаппаратов отличаются ещё и тем, что задают процесс не температуры, как в выражении (2-23), а, наоборот, выделения тепла. Температуры же являются искомыми величинами. Таким образом, тепловой поток Q необходимо представлять в схеме замещения источником тока P, а перегрев тела над охлаждающей средой - в виде неизвестной величины.

Всему сказанному соответствует схема замещения, представленная на рисунке 2.5.

В случае системы двух однородных тел, например, масла и обмотки трансформатора, его схема замещения будет представлять каскад из двух четырехполюсников С - R_т.

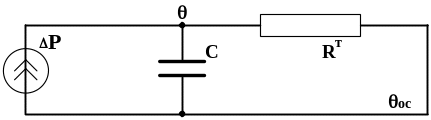
Рис. 2.5.