Лабораторна робота № 9 системи числення і способи переведення чисел із однієї системи числення в іншу

Мета роботи: придбання лабораторних навичок роботи на комп’ютері зі стандартною програмою операційної системи Windows: Калькулятор.

Завдання:

1. Ознайомитися з теоретичним матеріалом до теми.

2. Результати роботи подати у вигляді звіту.

3. Підготуватися до захисту роботи.

Послідовність виконання роботи:

1. Запустити програму Калькулятор.

2. Встановити режим «Обычный» і провести обчислення відповідно до варіанта завдання.

3. Встановити режим «Инженерный» і провести обчислення відповідно до варіанта завдання.

4. Результат обчислень запам’ятати у буфері обміну, а потім вставити зміст буфера в кінець нещодавно створеного текстового файлу „ПЗ_1.doc” (наприклад, A=123,09; B=7,6).

5. Зберегти файл.

Теоретичний матеріал до теми:

Калькулятор використовується для математичних обчислень і може мати два різні режими: «Обычный» або «Инженерный» (пункт меню Вид). Різниця полягає лише у кількості функцій, які використовуються. Результат обчислень можна запам’ятати у буфері обміну (пункт меню Правка → Копировать або з допомогою комбінації клавіш Ctrl+C), а потім вставити зміст буфера у відповідне місце будь-якого файлу (пункт меню Правка → Вставить або з допомогою комбінації клавіш Ctrl+V).

Системою числення (численням, нумерацією) називають систему прийомів і правил, що дозволяють встановити взаємно однозначну відповідність між будь-яким числом і його уявленням у вигляді сукупності кінцевого числа символів. Множини символів, що використовуються для такого уявлення, називають цифрами. Кожній цифрі відповідає певна кількість, що виразима цією цифрою і зветься чисельним значенням або кількісним еквівалентом даної цифри.

Розрізняють непозиційні і позиційні системи числення. В непозиційних системах має місце однозначна відповідність між цифрами і їх кількісними еквівалентами, а будь-яке число визначається як деяка функція від кількісних еквівалентів сукупності цифр, що зображають це число. Якщо як ця функція використовується функція додавання, то систему називають адитивною, якщо ж використовується функція множення, систему називають мультиплікативною. Прикладами непозиційних адитивних систем числення є римська система і одинична (унітарна) система.

Проте непозиційні системи не набули значного поширення в ЦОТ, оскільки вони характеризуються дуже складними і громіздкими алгоритмами подання чисел і виконання арифметичних операцій.

Систему числення називають позиційною, якщо одна і та ж цифра може відповідати різним кількісним еквівалентам залежно від номера місцеположення (розряду) цієї цифри в сукупності цифр, що зображають задане число. Позиційні системи розділяють на однорідні і змішані. У всіх розрядах числа, поданого в однорідній системі, використовуються цифри з однієї і тієї ж множини. Наприклад, в звичній десятковій системі у всіх розрядах будь-якого числа використовуються цифри з множини {0, 1, ..., 9}, у двійковій системі — цифри з множини {0, 1} тощо. У змішаних системах безліч цифр різна для різних розрядів. Прикладами змішаних систем є система для вимірювання кутів і дуг (в розрядах хвилин і секунд можуть бути використано 60 різних цифр, в розряді градусів — 360 різних цифр), система вимірювання часу, наприклад, в тисячоліттях, сторіччях, роках, місяцях, тижнях, добі, годиннику, хвилинах, секундах, десятих, сотих частках секунди.

Коли в позиційній системі для кожної цифри є окремий символ, її називають системою з безпосереднім поданням цифр. Існують також позиційні системи з кодованим поданням цифр. В таких системах кількість символів менше, ніж кількість цифр, а кожна цифра кодується певною комбінацією декількох символів, що є, як правило, цифри іншої системи числення. Наприклад, в змішаній системі вимірювання дуг і кутів кожна цифра розряду градусів кодується трьома десятковими символами, а в розрядах хвилин і секунд — двома десятковими символами.

Переважне поширення в ЦОТ набули однорідні позиційні системи числення. В такій системі з безпосереднім поданням цифр будь-яке число X виражається у вигляді

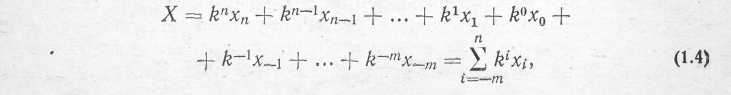
де k — основа системи числення, тобто кількість цифр, що використовуються в даній системі (k= 2, 3, ...); х — цифри i-го розряду подання числа в системі з основою k. Величину kⁱ прийнято називати вагою i-го розряду. Оскільки значення k відомо наперед, то вираз (1.4) запишемо в простішій формі

У виразі (1.5) кома відділяє цілу частину числа (n+1 розрядів) від дробової (m розрядів), а вага i-го розряду в k разів більша вага i-1-го розряду. Таку систему числення називають системою з природним порядком ваг. Існують системи з штучним порядком ваг, для яких вказане співвідношення ваг сусідніх розрядів не є обов’язковим. Відомі, наприклад, системи з штучним порядком ваг, в яких ціле позитивне число X виражається так:

Позиційні однорідні системи з природним порядком ваг розділяють також на системи з натуральними, негативними, дробовими і комплексними основами. Подання числа в якій-небудь системі числення називають кодом.

Системи числення з натуральною основою, в яких має місце взаємно однозначна відповідність між числом і його кодом кінцевої довжини, одержуваним за кінцеве число кроків, називають канонічними. В канонічних системах числення при записі чисел в кожному розряді може бути використана одна з до різних цифр, включаючи цифру 0. Позиційні системи числення з природним порядком ваг, в яких кількість різних допустимих цифр перевищує основу k, називають надлишковими. Надлишкові системи використовують в ЦОТ з метою підвищення надійності обробки інформації і швидкості виконання арифметичних операцій. В таких системах одному числу може відповідати декілька кодів кінцевої довжини, але одному коду відповідає одне число: Якщо кількість різних цифр у надлишковій системі дорівнює k + 2 і при цьому k = 2l, , або k = 2l+l, , то таку с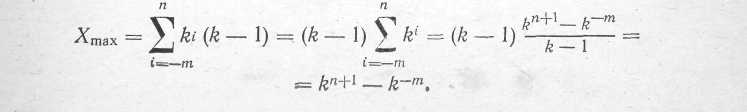 истему називають квазіканонічною.

Найбільше розповсюдження в практиці обчислювальних робіт отримала десяткова позиційна однорідна система числення. Проте ця система не є найзручнішою для реалізації її в ЕОМ, де, як правило, використовують системи числення з не десятковою основою — двійкова, вісімкова і інші, а також двійково кодовані системи (тобто такі системи, цифри яких закодовані двійковими символами). Пояснюється це в першу чергу простотою, високою надійністю і високою швидкодією технічних засобів, що використовуються для подання цифр і виконання операцій, що використовуються для подання, в двійковій системі числення. З порівняння цифрових ЕОМ різного призначення випливає, що звичайно машини, що вирішують задачі з відносно великим числом операцій введення—виведення, що доводяться на одну операцію з оброблення інформації, будують із використанням десяткової (двійково-десяткової) системи числення. В машинах же, що вирішують задачі, де час введення-виведення відносно невеликий в порівнянні з часом обробки інформації, застосовують двійкову систему числення. У зв’язку з цим виникає задача перетворення (переведення) чисел з однієї системи числення в іншу.

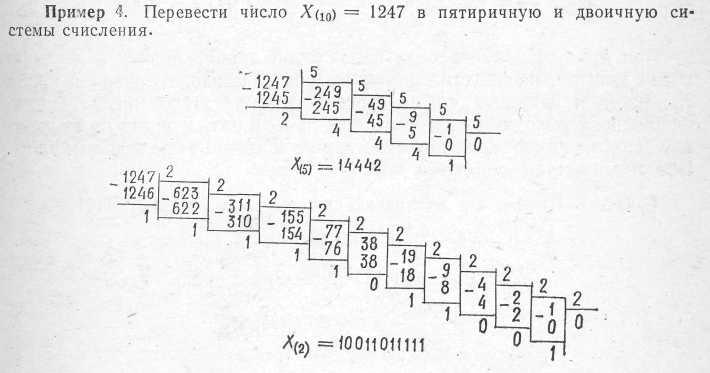
Неважко помітити, що права частина виразу (1.4) визначає правило обчислення кількісного еквівалента числа, записаного у формі (1.5). На цьому заснований один з алгоритмів переведення чисел з однієї позиційної системи в іншу. Позначимо X(k₁) число в k₁-й системі числення. Для переведення числа в систему з основою k₂ необхідно записати X_(ki) у формі (1.4), замінити цифри x_i і основу k₁ їх k₂-ми уявленнями, а потім виконати операції множення і додавання в системі з основою k₂. Розглянемо приклади.

Описаний спосіб переведення чисел з однієї системи в іншу одержав назву способу безпосереднього заміщення. Найбільше поширення цей спосіб набув у так званому табличному варіанті його реалізації. В цьому випадку в пам’яті ЕОМ зберігаються таблиці k₂-x подання k₁-x цифр і ступенів основи . Перевід чисел зводиться до вибірки з цих таблиць k₂-х еквівалентів цифр і ступенів основи, а також до виконання додавання і множення за правилами k₂-ї арифметики. Цей спосіб зручно використовувати у разі, коли k₁ < k₂ і при переводі чисел в таку систему, де просто виконуються операції додавання і множення (наприклад, із двійкової системи в десяткову). Для спрощення обчислень при цьому можна скористатися таким виразом, одержаним з (1.4):

Проте при переводі чисел в системи з «незвиклими» основами, особливо у разі k₁ > k₂, вживання цього способу пов’язано з досить громіздкими обчисленнями. Тому у багатьох випадках зручніше користуватися окремими способами переведення цілих чисел і правильних дробів.

Спосіб переведення цілих чисел з системи з основою k₁ в систему з основою k₂, (k₁ > k₂), полягає в наступному. Число X(k1) ділять на k₂ за правилами ділення з основою k₁ до отримання залишку. Якщо часткове від ділення не нуль, то часткове стає діленим і процес ділення на k₂ продовжують. Як тільки чергове часткове стане рівним нулю, процес ділення на k₂ припиняють. Залишок, одержаний при першому діленні на k₂, представляє цифру розряду результату з вагою , залишок від другого ділення представляє цифру результату з вагою тощо. Останній залишок є цифрою результату, що має вагу .

У разі, коли k₁ < k₂, виконують множення цифри з вагою числа X_(k1) (старшої цифри числа X_(k1)) на основу k₁, після чого до добутку додають наступну (в порядку убування ваг) цифру числа X_(ki). Результат попередньої операції множать на k₁ і додають чергову цифру числа X_(ki). Цей процес закінчують, коли буде додана цифра з вагою (молодша цифра). Всі обчислення при цьому виконуються в k₂-й системі числення.

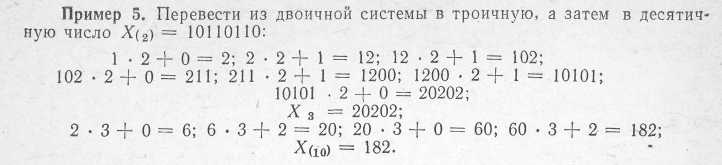
Перевід правильних дробів з системи числення з основою k₁ в систему з основою k₂ (k₁ > k₂) здійснюється так. Дріб, відповідний числу X_(ki). множиться на k₂ за правилами множення в системі з основою k₁. В одержаному добутку відділяється ціла частина, яка може бути рівною нулю, а дробова частина знову множиться на k₂ із подальшим відділенням цілої частини. Ці операції повторюють або до отримання нульової дробової частини добутку, або до отримання необхідної кількості розрядів числа X_k2 в новій системі числення. Старша цифра результату переведення (тобто перша після коми) збігається з першою відокремленою цілою частиною, друга цифра результату —- з другою відокремленою цілою частиною тощо.

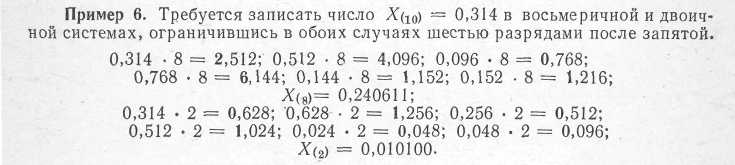
При k₁ < k₂ для переведення правильного дробу, що має m цифр після коми, необхідно розділити цифру молодшого розряду числа X_k1 на k₁ і скласти з наступною цифрою цього числа. Таку операцію необхідно повторити ще m-1 раз, використовуючи на кожному кроці як ділиме суми, одержаної на попередньому кроці. Всі операції виконуються в k₂-й системі.

У тому випадку, коли основи позиційних однорідних систем числення зв’язані співвідношенням k₁ = , де g > 0, перевід чисел виконується дуже просто. Якщо g — ціле, перевід зводиться до заміни кожної k₁-й цифри її g-розрядним k₂-м уявленням. При дробовому g початкове число розбивають на g — розрядні групи (починаючи з молодших розрядів) і кожну групу замінюють її k₂-м уявленням.

Приклад 8. Перевести з четвіркової системи в двійкову, а потім у шістнадцяткову число X₍₄₎ — 23013311. У шістнадцятковій системі кількісним еквівалентам 10, 11… 15 відповідають цифри А, В, ..., F.

Згідно вищевикладеному

X₍₂₎ = 1011000111110101;

X₍₁₆₎ = B 1 F 5.

Для переведення числа X з канонічної k₁-й системи числення в квазіканонічну систему з основою k₂ спочатку необхідно подати X у канонічній k₂-й системі. Потім ті цифри канонічної k₂-й системи, яких немає в квазіканонічній, замінюють комбінаціями цифр квазіканонічної системи. Після цього за правилами k₂-ї системи підсумовують всі одержані комбінації цифр з урахуванням їх ваг.

За результатами роботи оформити звіт, який повинен містити:

1. Титульний лист;

2. Тему и мету лабораторної роботи;

3. Завдання ;

4. Результати виконання завдання;

5. Висновки.

6. Список використаних джерел.

7. Зберегти звіт у власну папку з ім’ям „Прізвище_9.doc”.

8. Підготуватися до захисту роботи у викладача.