12Взаимные нормальные сечения. Уравнение геодезической линии

Геодезические линии, линии на поверхности, достаточно малые дуги которых являются на этой поверхности кратчайшими путями между их концами. На плоскости Геодезические линии — прямые, на круговом цилиндре — винтовые линии, на сфере— большие круги. Не всякая дуга Геодезические линии является на поверхности кратчайшим путём; например, на сфере дуга большого круга, большая полуокружности, не будет на этой сфере кратчайшей между своими концами. Геодезические линии обладает тем свойством, что их главные нормали являются нормалями к поверхности. Геодезические линии впервые появились в работах И. Бернулли и Л. Эйлера. Т. к. определение Геодезические линии связано только с измерениями на поверхности, они относятся к объектам т. н. внутренней геометрии поверхности. Понятие Геодезические линии переносится в геометрию римановых пространств. Советские математики А. Д. Александров и А. В. Погорелов исследовали аналоги Геодезические линии на общих выпуклых поверхностях. Понятие Геодезические линии широко применяется в теоретических и практических вопросах геодезии. Точки земной поверхности проектируются на поверхность земного эллипсоида и соединяются Геодезические линии При этом применяются некоторые специальные приёмы для перехода от расстояний и углов на земной поверхности к соответствующим дугам Геодезические линии и углам между ними на поверхности земного эллипсоида.

13Обратная угловая засечка. Решение задачи Ганзена

К элементарным измерениям относится и измерение угла β на определяемой точке P между направлениями на два пункта A и B с известными координатами X_A, Y_A и X_B, Y_B (рис. 2.10). Однако, это измерение оказывается теоретически довольно сложным, поэтому рассмотрим его отдельно.

Проведем окружность через три точки A, B и P. Из школьного курса геометрии известно, что угол с вершиной на окружности измеряется половиной дуги, на которую он опирается. Центральный угол, опирающийся на ту же дугу, измеряется всей дугой, следовательно, он будет равен 2β (рис. 2.10).

Рис. 2.10

Расстояние b между пунктами A и B считается известным, и из прямоугольного треугольника FCB можно найти радиус R окружности:

                  (2.41)

Уравнение окружности имеет вид:

                 (2.42)

где X_C и Y_C - координаты центра окружности. Их можно вычислить, решив либо прямую угловую, либо линейную засечку с пунктов A и B на точку C. В уравнении (2.42) X и Y - координаты любой точки окружности, в том числе и точки P, но для нахождения двух координат точки P одного такого уравнения недостаточно.

Обратной угловой засечкой называют способ определения координат точки P по двум углам β₁ и β₂, измеренным на определяемой точке P между направлениями на три пункта с известными координатами A, B, C (рис. 2.11).

Графическое решение. Приведем способ Болотова графического решения обратной угловой засечки. На листе прозрачной бумаги (кальки) нужно построить углы β₁ и β₂ с общей вершиной P; затем наложить кальку на чертеж и, перемещая ее, добиться, чтобы направления углов на кальке проходили через пункты A, B, C на чертеже; переколоть точку P с кальки на чертеж.

Исходные данные: X_A, Y_A, X_B,

                                    Y_B, X_C, Y_C;

Измеряемые элементы: β₁, β₂.

Неизвестные элементы: X, Y.

Рис. 2.11

Аналитическое решение. Аналитическое решение обратной угловой засечки предусматривает ее разложение на более простые задачи, например, на 2 прямых угловых засечки и одну линейную, или на 3 линейных засечки и т.д. Известно более 10-ти способов аналитического решения, но мы рассмотрим только один - через последовательное решение трех линейных засечек.

Предположим, что положение точки P известно, и проведем две окружности: одну радиусом R₁ через точки A, B и P и другую радиусом R₂ через точки B, C и P (рис. 2.11). Радиусы этих окружностей получим по формуле (2.41):

              (2.43)

Если координаты центров окружностей - точек O₁ и O₂ будут известны, то координаты точки P можно определить по формулам линейной засечки: из точки O₁ по расстоянию R₁ и из точки O₂ - по расстоянию R₂.

Координаты центра O₁ можно найти по формулам линейной засечки из точек A и B по расстояниям R₁, причем из двух решений нужно взять то, которое соответствует величине угла β₁: если β₁<90^o, то точка O₁ находится справа от линии AB, если β₁>90^o, то точка O₁ находится слева от линии AB.

Координаты центра O₂ находятся по формулам линейной засечки из точек B и C по расстояниям R₂, и одно решение из двух возможных выбирается по тому же правилу: если β₂<90^o, то точка O₂ находится справа от линии BC, если β₂>90^o, то точка O₂ находится слева от линии BC.

Задача не имеет решения, если все четыре точки A, B, C и P находятся на одной окружности, так как обе окружности сливаются в одну, и точек их пересечения не существует.

В задаче Ганзена находят координаты двух точек P и Q по известным координатам двух пунктов A и B и четырем углам, измеренным на определяемых точках (рис. 2.15), то есть, задача Ганзена является сдвоенной обратной угловой засечкой.

Исходные данные: X_A, Y_A, X_B, Y_B.

Измеренные элементы: β₁, β₂, β₃, β₄.

Неизвестные элементы: X_P, Y_P, X_Q, Y_Q.

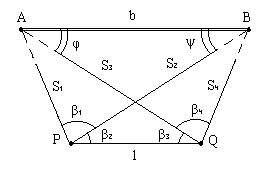
Рис. 2.15. Схема задачи Ганзена

Графическое решение. Взять два листа прозрачной бумаги (кальки) и построить на них углы: на одном листе - углы β₁ и β₂, на другом листе - углы β₃ и β₄. Наложить на чертеж (план или карту) оба листа и, перемещая их произвольным образом, совместить направления углов на этих листах с точками А и В на чертеже. Переколоть точки P и Q на чертеж.

Аналитическое решение. Известно несколько способов решения задачи Ганзена; приведем краткое изложение одного из них.

1. Решить обратную задачу между пунктами A и B, то есть, вычислить длину b отрезка AB и дирекционный угол α_AB направления AB.

2. Ввести условную единицу длины, равную длине l отрезка PQ; l = 1.000 .

3. Вычислить отрезки S'₁ = AP, S'₃ = AQ, S'₂ = BP, S'₄ = BQ в условных единицах с использованием теоремы синусов сначала для треугольника PAQ, затем для треугольника PBQ:

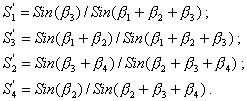             (2.55)

4. Вычислить в условных единицах длину b' отрезка AB из треугольника QAB по теореме косинусов:

               (2.56)

и для контроля - из треугольника PAB:

                (2.57)

Оба значения должны совпасть.

5. Вычислить масштабный коэффициент k:

k = b / b'                   (2.58)

и перевести все вычисленные расстояния в реальные единицы длины:

               (2.59)

6. Вычислить угол φ из треугольника QAB по теореме косинусов:

              (2.60)

7. Вычислить угол ψ из треугольника PAB по теореме косинусов:

                (2.61)

8. Вычислить дирекционный угол направления AQ:

                 (2.62)

и решить прямую геодезическую задачу с пункта A на точку Q :

                (2.63)

9. Вычислить дирекционный угол направления BP α_BP= α_BA - φ и решить прямую геодезическую задачу с пункта B на точку P:

10. Расположение исходных пунктов и определяемых точек может быть таким, что отрезки PQ и AB будут пересекаться (рис.2.16); ход решения задачи остается таким же, только изменятся обозначения углов и сторон. Кроме того, доказано, что в этом варианте положение точек P и Q определяется в несколько раз точнее, чем в общем варианте.

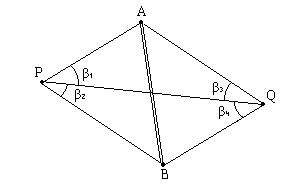
Рис. 2.16. Вариант задачи Ганзена

В однократной задаче Ганзена отсутствует контроль измерений, поэтому на практике четырьмя измерениями углов не ограничиваются, а выполняют какие-либо дополнительные измерения.