17.2. Оптимизационное проектирование

Из всех возможных вариантов при проектировании конструктор должен выбрать оптимальный. Оптимизация, по существу, является главной задачей конструктора.

С применением ЭВМ расширяется объем используемой информации, возрастает значение анализа влияния различных параметров на качественные показатели, на основе которого могут приниматься обоснованные решения.

При автоматизированном проектировании пользователь ставит задачу для ЭВМ и принимает окончательное решение, а машина обрабатывает весь объем информации и делает первичный отбор. Повышаются производительность и качество труда конструктора, ускоряются поиск и выбор оптимального варианта.

Наиболее проста однокритериальная оптимизация, проводимая по одному доминирующему критерию. Она позволяет выделить наиболее важные критерии и параметры, влияющие на качество проектируемого изделия, сократить их число и облегчить многокритериальную оптимизацию, проводимую по нескольким критериям.

В основном проводят параметрическую оптимизацию, при которой обеспечиваются оптимальные параметры элементов заданной структуры (например, параметры редуктора заданной схемы) без изменения самой структуры (без изменения схемы редуктора).

САПР предполагает активное участие человека в анализе вариантов, оптимизации, принятии решений. Такой творческий подход может быть реализован при курсовом проектировании, например, на базе программ по расчету передач [9, 11].

В программах проектного расчета зубчатых и червячных передач вычисления производятся с перебором значений (варьированием) наиболее значимых параметров: способа термической обработки или применяемых материалов (допускаемых напряжений), коэффициента ширины зубчатого венца, распределения общего передаточного числа между ступенями. Пользователю необходимо провести анализ влияния этих параметров на качественные показатели и с учетом налагаемых ограничений выбрать оптимальный вариант.

В качестве критерия оптимальности наиболее часто принимают массу изделия. Масса характеризует материалоемкость, она тесно связана с габаритами (объемом) изделия и трудоемкостью его изготовления, а стоимость материала составляет значительную часть стоимости машины. Особое значение уменьшение массы имеет для транспортных машин, летательных аппаратов.

Выбор варианта выполняют с учетом следующих общих ограничений:

- возможности конструктивного решения выбранного варианта;

- дефицитности материалов (для редукторов общепромышленного применения предпочтительны малолегированные стали и безоловянные бронзы, особенно при крупносерийном производстве);

- технологических возможностей производства (наличие соответствующего оборудования для зубонарезания; при высокой твердости материала колес необходимы отделочные операции: шлифование, притирка поверхностей зубьев);

- соразмерности узлов и деталей привода (электродвигателя, редуктора, ременной или цепной передачи, приводного вала и др.), которая обусловлена требованиями целесообразности и технической эстетики.

Под конструктивными ограничениями понимают прежде всего возможность изготовления зубьев шестерни и обеспечение необходимой прочности и жесткости входного (быстроходного) вала, возможность размещения в корпусе редуктора подшипников валов быстроходной ступени. Чем больше передаточное число Мре_Д редуктора и выше поверхностная твердость зубьев, тем труднее удовлетворить конструктивным ограничениям.

Исходя из обеспечения необходимой прочности и жесткости вычисляют диаметр d (мм) концевого участка входного (быстроходного) вала

(17.1)

где К = 7 для цилиндрических и К = 8 для конических передач; Т_Б -вращающий момент на валу, Н ∙ м.

В связи с обычным по соображениям жесткости увеличением диаметра вала от концевого участка к участку расположения шестерни необходимо выполнение условия (здесь d вычисляют по формуле (17.1)):

- для шестерни цилиндрической передачи редуктора

d_f1≥ 1,25d; (17.2)

- для передвижной шестерни цилиндрической ступени коробки передач

d_f1≥ 1,8d (17.3)

- для шестерни конической передачи

d_f1 ≥ 1,35 d. (17.4)

Ниже приведены рекомендации по выбору рационального варианта для отдельных типов редукторов.

Конический редуктор. В качестве вариантов термообработки шестерни и колеса рассматривают улучшение, закалку с нагревом ТВЧ, цементацию. В соответствии с программой производится расчет передачи по контактным напряжениям с проверкой по напряжениям изгиба, в результате чего определяют: размеры и массу зубчатых колес, габариты корпуса редуктора, массу всего редуктора. Вид термообработки оказывает существенное влияние на перечисленные параметры. Так, например, у цементованных колес по сравнению с улучшенными масса уменьшается в 2,5 ... 3 раза, однако масса редуктора снижается ~ 20 %, так как большая часть массы одноступенчатого редуктора приходится на корпус и валы.

По результатам расчета следует установить зависимость (построить график) массы зубчатых колес и всего редуктора, а также среднего делительного диаметра d_m1 шестерни от вида термообработки.

При выборе рационального варианта необходимо отдать предпочтение варианту с меньшей массой, удовлетворяющему, кроме общих, дополнительным конструктивным ограничениям:

средний делительный диаметр шестерни должен удовлетворять условию (17.4);

для обеспечения соразмерности редуктора и деталей, устанавливаемых на концах входного и выходного валов необходимо, чтобы диаметр ведомого шкива ременной или диаметр ведущей звездочки цепной передачи не превышали более чем на 20 % диаметр d_ae2 вершин зубьев колеса.

Цилиндрический редуктор. В качестве варьируемых параметров могут использоваться варианты термообработки, относительная ширина ψ_ba зубчатых колес. Для анализа строят графические зависимости массы зубчатых колес и всего редуктора от вида термообработки при различных значениях коэффициента ψ_ba .

При выборе рационального варианта необходимо отдать предпочтение варианту с меньшей массой, удовлетворяющему, кроме общих, дополнительным конструктивным ограничениям:

- диаметр d_f] впадин зубьев шестерни должен удовлетворять условию (17.2);

• для обеспечения соразмерности редуктора и деталей, устанавливаемых на концах входного и выходного валов, необходимо, чтобы диаметр ведомого шкива ременной или диаметр ведущей звездочки цепной передачи не превышали более чем на 20 % диаметр d_a2 вершин зубьев колеса;

• должно быть обеспечено размещение в корпусе редуктора подшипников валов передачи с возможной установкой между подшипниками болта крепления крышки и корпуса редуктора (при плоскости разъема корпуса по осям валов).

Коробка передач. Анализ проводят так же, как для цилиндрического одноступенчатого редуктора, но с проверкой выполнения условия (17.3) и учетом того, что колеса в коробках передач уже, чем в редукторах.

Планетарный редуктор. Так же, как и для цилиндрического, основное влияние на массу редуктора оказывает вид термообработки.

В качестве рационального нужно выбрать вариант с меньшей массой, но с возможностью размещения подшипника в сателлите, оценкой соразмерности солнечной шестерни и входного вала, эпицикла и детали, устанавливаемой на конце выходного вала.

Червячный редуктор. При расчете определяют: межосевое расстояние, размеры червяка и колеса, КПД передачи, температуру масла в редукторе.

Расчет проводится последовательно для разных материалов венца червячного колеса: БрО10Ф1, БрО5Ц5С5, БрА9ЖЗЛ. Наиболее целесообразным является вариант с возможно меньшей массой и большим КПД при допустимой температуре масла в редукторе, с оценкой целесообразности установки вентилятора на быстроходном валу и соразмерности редуктора и деталей, устанавливаемых на концах входного и выходного валов.

Двухступенчатый цилиндрический (коническо-цилиндри-ческий) редуктор. При проектировании двухступенчатых редукторов необходимо решить вопрос о распределении известного общего передаточного числа u _ред редуктора между быстроходной u_Б и тихоходной u_т ступенями (u _ред = u_Б u_т ). Поэтому в программе предусматривается проведение расчетов при разных способах термообработки зубчатых колес и разных отношениях u_Б / u_т .

Наибольшее влияние на массу редуктора оказывает термообработка. Закалка зубчатых колес с нагревом ТВЧ по сравнению с улучшением снижает массу редуктора в ~1,2 раза, а цементация в ~1,7 раза. Меньшее влияние оказывает распределение общего передаточного числа u_ред, а влияние относительной ширины колес невелико: при любой термообработке колес при изменении ψ_ba от 0,3 до 0,6 масса редуктора изменяется на ~10 %.

Термообработка оказывает существенное влияние на металлоемкость колес. Так, цементация с последующей закалкой по сравнению с улучшением снижает массу колес в 3,5 раза. При этом масса редуктора, как было сказано выше, изменяется меньше, так как масса улучшенных зубчатых колес составляет 30 ... 40 % общей массы редуктора, а цементованных — 15 ... 20 %.

Для оценки результатов счета строят графики, отражающие влияние распределения передаточного числа u_ред между ступенями, вида термообработки зубчатых колес на основные качественные показатели: массу m_k зубчатых колес, массу т_ред редуктора,

суммарное межосевое расстояние a_wc = a_wБ + a_wТ диаметр d_f1 впадин зубьев быстроходной шестерни, диаметры d_a2B и d_a2T вершин зубьев колес быстроходной и тихоходной ступеней.

Поиск варианта с наименьшей массой редуктора должен предусматривать выполнение следующих конструктивных ограничений:

- диаметр d_f1 (или d_m1) впадин зубьев шестерни быстроходной ступени должен удовлетворять условию (17.2) (или (17.4));

- должно быть обеспечено размещение в корпусе редуктора подшипников валов быстроходной и тихоходной ступеней; между подшипниками валов тихоходной ступени должен быть размещен болт крепления крышки и корпуса редуктора (при плоскости разъема корпуса по осям валов);

- при смазывании зацеплений погружением в масляную ванну зубчатых колес обеих ступеней разность ΔR = диаметров вершин зубьев колес соответственно тихоходной и быстроходной ступеней должна быть по возможности меньше при выполнении условия ΔR ≤ 0,25d_a2T .На рис. 17.1 приведены графики, построенные по результатам расчета двухступенчатого цилиндрического редуктора, выполненного по развернутой схеме, для трех способов термообработки зубьев шестерни и колеса и трех способов распределения передаточного числа u_ред = u_Бu_т между ступенями редуктора (трех значений отношения u_Б/u_т ): всего девять вариантов.

На графиках римскими цифрами обозначены следующие сочетания твердостей рабочих поверхностей зубьев шестерни и колеса, соответствующие способу термической обработки: I - улучшение шестерни и улучшение колеса (H_]ср = 28,5HRC,

Н_2ср - 24,8HRC); II - закалка с нагревом ТВЧ шестерни и улучшение колеса (H_1ср = 47,5HRC, H_2ср = 28,5HRC); III - цементация шестерни и колеса (H_1ср = 59HRC, H_2ср = 59HRC).

На рис. 17.1, а проведена штриховая линия, соответствующая минимально допустимому значению диаметра d_f1 впадин зубьев быстроходной шестерни по условию (17.2). В качестве оптимального следует выбрать вариант с меньшей массой m_ред редуктора из числа тех, что расположены выше штриховой линии и удовлетворяют условию ΔR ≤ 0,25d_a2T . Поэтому для конструктивной проработки рекомендуется принять вариант 5 (см. рис. 17.1, б, г).

При выполнении расчетов передач редукторов с одновременным выбором электродвигателя вычисления проводят при различных частотах вращения валов электродвигателей одной и той же мощности. Масса т_э двигателя при этом тем меньше, чем выше частота вращения вала. Но необходимость реализации большего передаточного числа u_ред приводит к увеличению массы т_ред редуктора. Поэтому оптимальным является вариант с минимальной суммарной массой привода т_сум =т_э + m_ред.

Поиск варианта с наименьшей суммарной массой привода должен предусматривать выполнение перечисленных выше конструктивных ограничений для двухступенчатого редуктора.

При нескольких влияющих параметрах целесообразно проводить поиск оптимальных решений на ЭВМ с выдачей результатов в графическом виде на экране или на бумаге с помощью графопостроителя.

Рассмотрим программу оптимизации двухступенчатого редуктора, выполненного по развернутой схеме. В качестве варьируемого параметра рассматриваем распределение передаточных чисел между быстроходной u_Б и тихоходной и_Т ступенями при заданном общем передаточном числе u_ред = и_Би_Т редуктора. Изменение в распределении передаточных чисел между ступенями характеризуется отношением u_Б/u_т .

В качестве критериев оптимальности примем:

- длину L и площадь А основания редуктора (исходя из рационального использования площади цеха);

- объем V редуктора (что соответствует его массе);

- массу М_к зубчатых колес.

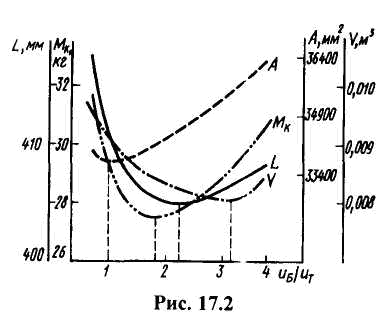
Как показывает анализ, каждый из критериев имеет минимум, который достигается при вполне определенном распределении передаточных чисел между ступенями. На рис. 17.2 приведены зависимости критериев L, А, V, М_к от отношения u_Б/u_т, полученные по результатам расчета двухступенчатого цилиндрического редуктора на сопротивление контактной усталости при следующих исходных данных: вращающий момент на выходном валу T₂ = 420 Н•м, общее передаточное число редуктора u_ред = 20, допускаемые контактные напряжения при расчете быстроходной и тихоходной ступеней [σ]_НБ = [σ]_НТ = 600 Н/мм². Из анализа рис. 17.2 следует, что могут быть получены минимальные значения критериев:

площади основания (А_min) при и_Б/и_T = 1(и_Б=и_Т =4,47);

массы колес (M_Kmin) при u_Б/u_т = 1,75(u_Б =5,91;u_т =3,38);

длины редуктора (L_min) при u_Б/u_т = 2,2 (u_Б = 6,64; и_T = 3,02);

объема редуктора (V_min) при u_Б/u_т = = 3,1 (u_Б= 7,88; и_T = 2,54).

С увеличением общего передаточного числа u_ред минимальным значениям критериев А, М_к, L, V соответствуют большие значения отношения u_Б/u_т, т.е. большие передаточные числа быстроходной ступени u_Б и соответственно меньшие значения u_т (рис. 17.3).

Рис. 17.3.

Более нагруженные зубчатые колеса тихоходной ступени могут иметь другую термообработку и большие допускаемые напряжения [σ]_НБ. С ростом напряжений [σ]_HT отношения u_Б/u_т , соответствующие минимальным значениям критериев А, М_к, L, V, смещаются в область меньших значений (рис. 17.4).

Таким образом, оптимальное распределение передаточных чисел между ступенями двухступенчатого редуктора зависит как от общего передаточного числа u_ред , так и от соотношения допускаемых контактных напряжений [σ]_НБ быстроходной и [σ]_НТ тихоходной ступеней.

От передаточных чисел ступеней, в свою очередь, зависят размеры зубчатых колес, диаметр промежуточного вала, определяемый из расчета по передаваемому вращающему моменту. Поэтому следующей важной задачей является проверка возможности реализации варианта, выбранного по минимальному значению какого-либо критерия, путем сопоставления получаемых расчетом результатов с принятыми конструктивными ограничениями.

В качестве конструктивных ограничений рассматриваются (рис. 17.5):

условие размещения подшипников валов быстроходной ступени (при необходимости с учетом расположения между ними болта соединения крышки и корпуса редуктора) - параметр Δ_ПБ;

- условие размещения колеса быстроходной ступени - параметр Δ _а ;

- условие размещения подшипников валов тихоходной ступени - параметр Δ_ПТ;

- условие изготовления неврезной шестерни быстроходной ступени.

Последнее из перечисленных ограничений не является жестким. При исполнении программы пользователь информируется о получаемых размерах d₁ и d_в1 где d₁ - диаметр делительной окружности шестерни быстроходной ступени, d_в1 - диаметр входного (быстроходного) вала в месте расположения шестерни. При его согласии может быть принято конструктивное исполнение с врезной шестерней.

Допустимые значения параметров устанавливает пользователь, например: Δ_ПБ ⁼ 15 мм; Δ _а = 10 мм; Δ_ПТ = 15 мм [Δ_п = 2(Т₂)^1/3 ].

На рис. 17.6 показан характер изменения числовых представлений конструктивных ограничений в зависимости от распределения передаточных чисел (отношения и_Б/и_Т ). Из рис. 17.6 следует, что с уменьшением отношения и_Б/и_Т (с уменьшением передаточного числа быстроходной ступени) проще удовлетворить конструктивные ограничения, связанные с размещением колеса быстроходной ступени (Δ _а), а также подшипников валов тихоходной ступени (Δ_ПТ), проще получить неврезное исполнение быстроходной шестерни (d₁), но труднее выполнить условие размещения подшипников валов быстроходной ступени (Δ_ПБ), так как с уменьшением и_Б/и_Т величина Δ_ПБ уменьшается.

На параметры Δ_ПБ, Δ_ПТ, Δ_а, d₁ значительное влияние оказывает величина допускаемых контактных напряжений. Значения этих параметров уменьшаются с увеличением контактных напряжений [σ]_н - при высоких значениях [σ]_н труднее удовлетворить конструктивным ограничениям. Общее передаточное число u_ред сильно влияет на размер быстроходной шестерни (d₁ при u_ред = 31,5 в 1,6 раза меньше, чем при u_ред = 12,5), слабо влияет на условие размещения под шипников и не оказывает влияния на условие размещения колеса быстроходной ступени.

Работа по программе предусматривает поиск отношения и_Б/и_T , соответствующего минимальному значению каждого из четырех выделенных критериев (А_min, М_{k min}, L_min, V_min), с последующей проверкой удовлетворения конструктивных ограничений.

Если для рассматриваемого критерия не обнаружено противоречия ни одному из ограничений, то конструктивная схема с минимальным значением критерия вычерчивается на графопостроителе, а на печать выводятся дополнительные сведения (и_Б, и_T, размеры и масса колес и др.).

Если же не удовлетворяется любое из наложенных ограничений, то в этом случае выбирается конструктивная схема не с минимальным значением критерия, а с наименьшим возможным по условию удовлетворения лимитирующего (одного или нескольких) ограничения.

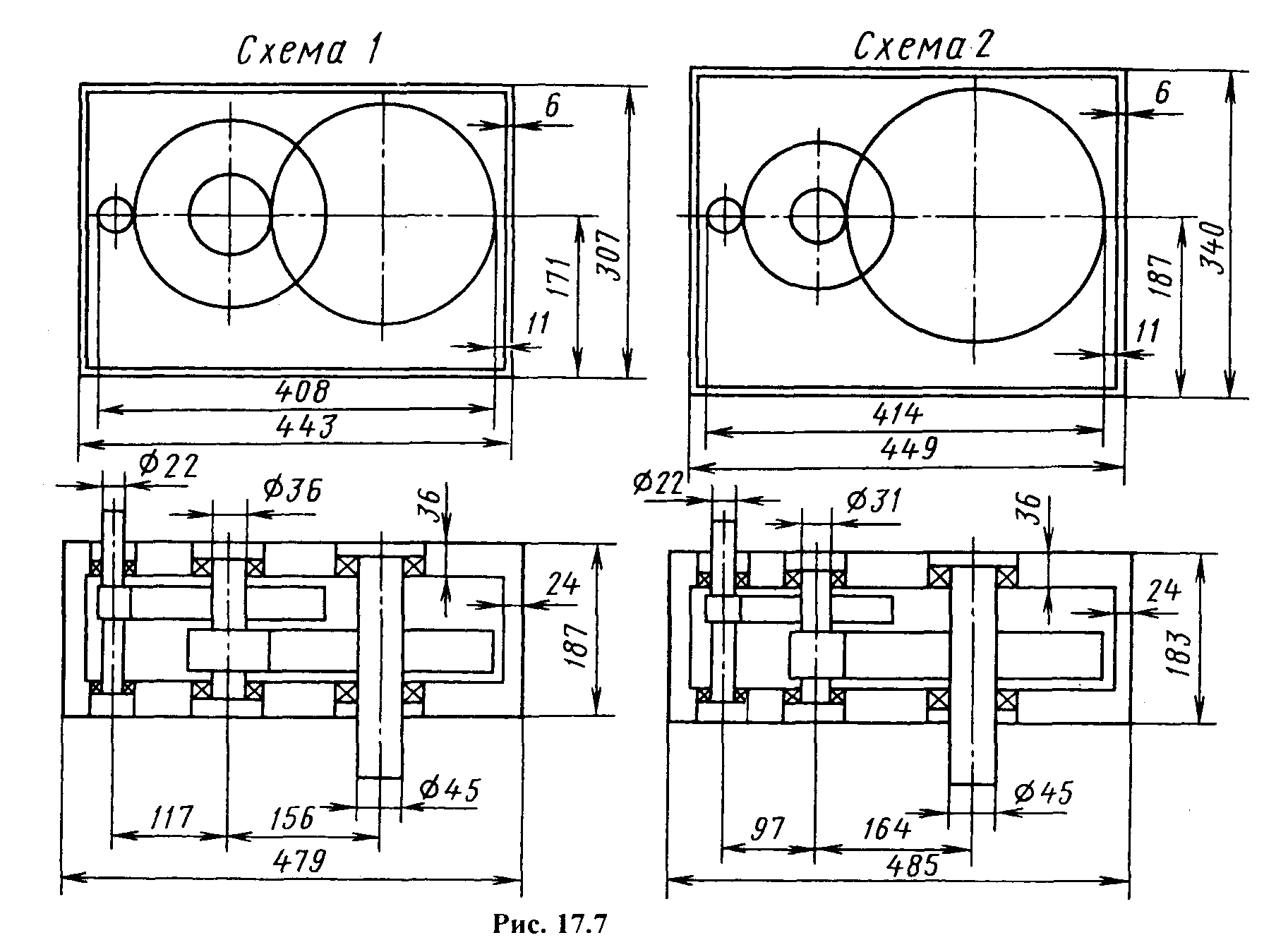
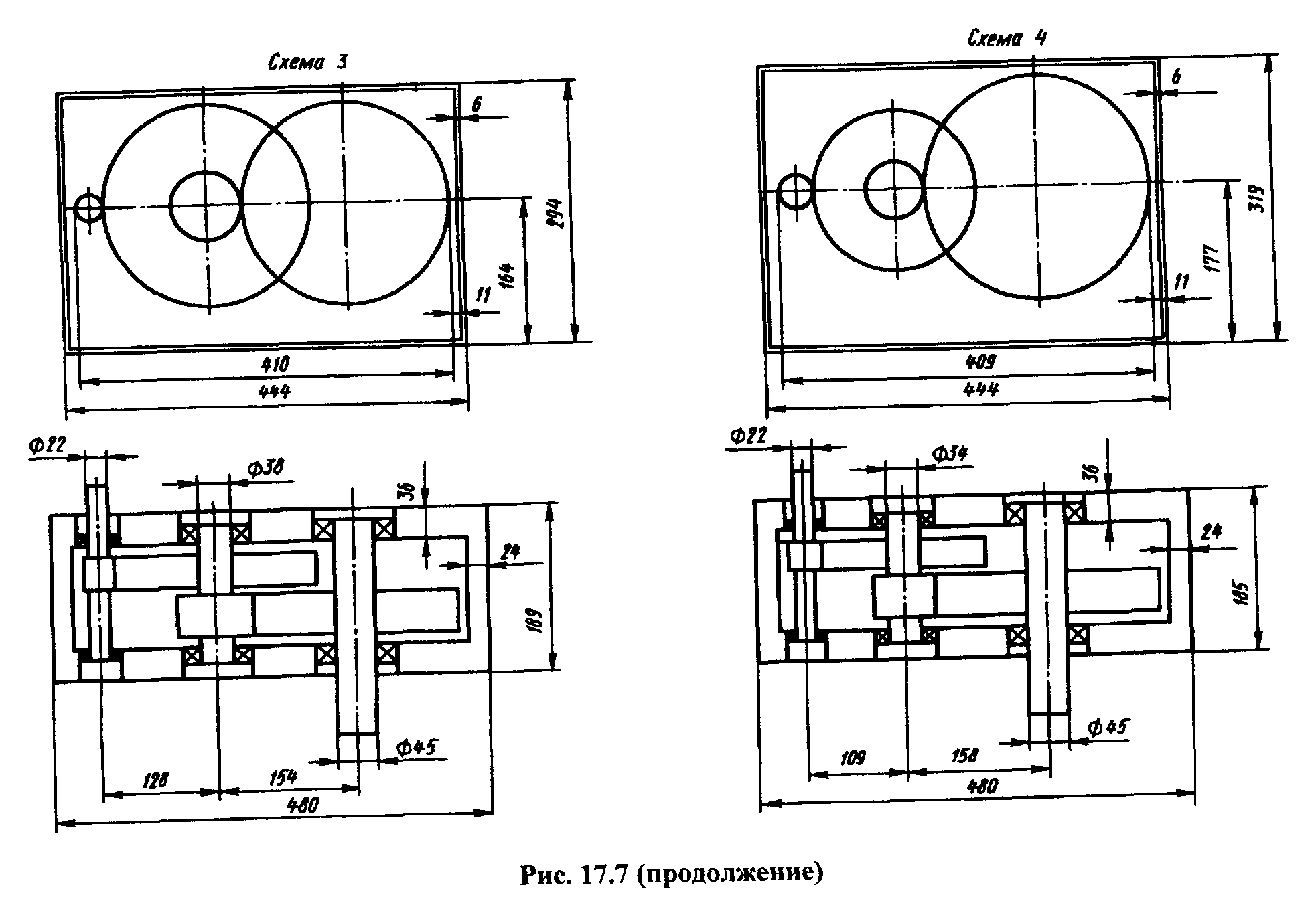
Масштаб изображения компоновочной схемы на графопостроителе задает пользователь. На рис. 17.7 приведены в качестве примера компоновочные схемы для следующих исходных данных: вращающий момент на выходном валу T₂ = 420 Н•м, [σ]_HБ = 600 Н/мм², [σ]_HТ = 600 Н/мм², u_ред = 20, ψ_ba1= ψ_ba2 = 0,315 . Номера схем на рис. 17.7 соответствуют: 1 – L_min (и_Б = 6,2; и_т = 3,2); 2 -L_min(и_Б=4,2; и_т=4,7); 3 – V_min( и_Б = 7,3; и_т = 2,7); 4 -М_{к min}(и_Б =5,4; и_т =3,7).