Тема №7 «Фазові переходи. Явища переносу»

1. Поняття фазового переходу.

2. Діаграма стану.

3. Зміна агрегатного стану речовини.

4. Явища переносу.

5. Дифузія, теплопровідність, поверхневий натяг.

6. Термодинамічні та молекулярно-кінетичні методи дослідження сировини і матеріалів.

Фазовий перехід у фізиці означає таку трансформацію внутрішньої структури речовин, при якій відбувається різкий стрибок певної фізичної характеристики системи, викликаний малою зміною іншої характеристики. Розрізняють фазові переходи першого і другого роду.

П ри фазових переходах першого роду поглинається або виділяється прихована теплота. Фазові переходи другого роду відбуваються без поглинання чи виділення тепла. Така сучасна класифікація дещо відрізняється від класифікації Еренфеста, який назвав фазовими переходами першого роду переходи, при яких стрибком міняються перші похідні від вільної енергії, а фазовими переходами другого роду ті, при яких стрибком міняються, відповідно другі похідні від вільної енергії. Інші, відмінні від вільної енергії термодинамічні потенціали, наприклад, внутрішня енергія або ентальпія, при фазових переходах першого роду міняються стрибком. Недоліком класифікації Еренфеста є те, що при деяких фазових переходах похідні від вільної енергії прямують до нескінченності, наприклад теплоємність при фазовому переході до феромагнітного стану.

Прикладами фазових переходів є:

• зміна агрегатного стану (випаровування, сублімація і т.п.);

• перехід речовини до стану надплинності (коли речовина втрачає в’язкість);

• п 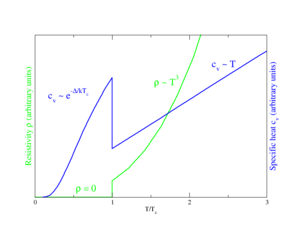ерехід до надпровідності;

Речовина	Т, К	Т, С
Вольфрам	0,012	-273,139
Галій	1,091	-272,059
Алюміній	1,14	-272,01
Індій	3,37	-269,78
Ртуть	4,153	-268,997
Свинець	7,193	-265,957

• п ерехід між феромагнетиком і парамагнетиком, сегнетоелектриком і діелектриком;

• перехід між рідкокристалічною фазою і фазою звичайної ізотропної рідини.

Для графічного зображення співвідношень між параметрами стану фізико-хімічної системи, що приводять до утворення різного складу речовини, служить спеціальний тип діаграм – діаграми стану (діаграми рівноваги, фазові діаграми). У простому випадку, коли система складається лише з одного компонента, діаграма стану є тривимірною просторовою фігурою, побудованою в трьох прямокутних координатних осях, по яких відкладають температуру (Т), тиск (p) і молярний об’єм (v). Користуватися об’ємною діаграмою стану незручно внаслідок громіздкості; тому на практиці застосовують її проекцію на одну з координатних площин, зазвичай на площину p-Т.

Діаграми стану показують стійкі стани, тобто стану, які за даних умов мають мінімум вільної енергії, і тому її також називають діаграмою рівноваги, тому що вона показує, які за даних умов існують рівноважні фази.

Побудова діаграм стану найбільше часто здійснюється за допомогою термічного аналізу. У результаті одержують серію криві охолодження, на яких при температурах фазових перетворень спостерігаються точки перегину й температурні зупинки.

Температури, що відповідають фазовим перетворенням, називають критичними точками. Деякі критичні точки мають назви, наприклад, точки кристалізації, що відповідають початку, називають точками ліквідус, а кінцеві кристалізації – точками солідус.

По кривих охолодження будують діаграму сполуки в координатах: по осі абсцис – концентрація компонентів, по осі ординат – температура.

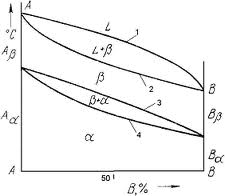
Шкала концентрацій показує зміст компонента В. Основними лініями є лінії ліквідус (1) і солідус (2), а також лінії відповідним фазовим перетворенням у твердому стані (3, 4). По діаграмі стану можна визначити температури фазових перетворень, зміна фазової сполуки, приблизно, властивості сплаву, види обробки, які можна застосовувати для сплаву.

Речовина може існувати в твердому, рідкому і газоподібному станах:

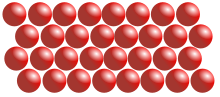
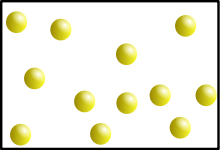
а) б) в)

У твердому стані (а) речовина зберігає форму і об’єм. В рідкому (б) форма не зберігається, а зберігається об’єм. В газоподібному стані (в) речовина ні форми, ні об’єму не зберігає.

Процес перетворення рідини в пару називається випаровуванням. Він відбувається з поглинанням певної кількості теплоти Q_n. Кількість теплоти Q, потрібної для перетворення в пару 1кг рідини при сталій температурі, називають питомою теплотою пароутворення:

. (7.1)

де L – питома теплота пароутворення, яку вимірюють у Дж/кг, m – маса речовини, яка випаровується.

Процес перетворення пари в рідину називається конденсацією. При конденсації пари виділяється певна кількість теплоти. Випаровуються не тільки рідини, а й тверді тіла. Випаровування твердих тіл називають сублімацією.

Якщо число молекул пари, які випаровуються, дорівнює числу молекул пари, які конденсуються за той самий час, то число молекул пари над рідиною буде сталим. Такий стан називають динамічною рівновагою пари і рідини.

Пара, що при незмінному об’ємі й сталій температурі перебуває в динамічній рівновазі зі своєю рідиною, називається насиченою, а відповідний тиск – тиском насиченої пари. Тиск насиченої пари залежить тільки від її температури. Ненасичена пара – це пара, тиск якої менший за тиск насиченої пари при даній температурі р < р_нас.

Повітря завжди містить певну кількість водяної пари. Кількість грамів водяної пари в 1м³ повітря називають абсолютною вологістю повітря. Крім абсолютної вологості, треба знати й ступінь насичення повітря парою. Він характеризується відносною вологістю повітря – величиною, що дорівнює відношенню парціального тиску р водяної пари, що знаходиться у повітрі, до тиску р_нас насиченої пари при тій самій температурі:

. (7.2)

Температуру t_p, при якій водяна пара стає насиченою, називають точкою роси. Нижче точки роси починається конденсація пари (випадає роса, виникає туман).

Відносну вологість повітря вимірюють психрометрами і гігрометрами.

Д ія психрометра заснована на залежності температури рідини від вологості навколишнього повітря. Він складається з двох термометрів – «сухого» і «вологого». «Вологий» термометр вимірює температуру зволоженого шматочка тканини, яким обгорнуто його кульку.

Швидкість випаровування вологи збільшується зі зменшенням відносної вологості повітря. Випаровування, в свою чергу, викликає охолодження об’єкта, з якого волога випаровується. При охолодженні вологого об’єкта зменшується і швидкість випаровування вологи до тих пір, доки при деякій температурі не буде досягнута динамічна рівновага – кількість вологи, яка випарується, зрівняється з кількістю вологи, яка конденсується. Отже, температура вологого об’єкта (наприклад, термометра, обгорнутого вологою тканиною) дає інформацію про відносну вологість повітря.

Сучасні психрометри можна розділити на три категорії: станційні, аспіраційні та дистанційні. У станційних психрометрах термометри закріплені на спеціальному штативі у метеорологічній будці. Основним їх недоліком є залежність показів зволоженого термометра від швидкості повітряного потоку в будці. В аспіраційному психрометрі термометри розташовані в спеціальній оправі, яка захищає їх від пошкоджень і теплового випромінювання навколишніх предметів, де вони обдуваються за допомогою аспіратора (вентилятора) потоком досліджуваного повітря з постійною швидкістю біля 2 м/с. Це найнадійніший прилад для вимірювання температури і вологості повітря. У дистанційних психрометрах використовують термометри опору (терморезистори).

Дія гігрометрів заснована на залежності певних фізичних параметрів (електричний опір, маса, довжина) деяких тіл від вологості навколишнього повітря.

Існує кільки видів гігрометрів, дія яких базується на різних принципах.

В аговий (абсолютний) гігрометр складається з системи U-подібних трубок, наповнених гігроскопічною речовиною, здатною поглинати вологу з повітря. Через цю систему насосом протягують певну кількість повітря, вологість якого визначають. Знаючи масу системи до і після вимірювання, а також об’єм пропущеного повітря, знаходять абсолютну вологість.

Дія волосяного гігрометра базується на властивості обезжиреної волосини змінювати свою довжину при зміні вологості повітря, що дозволяє вимірювати відносну вологість від 30 до 100%. Волосина натягнута на металеву рамку. Зміна довжин волосини передається стрілці, яка переміщується вздовж шкали.

Плівковий гігрометр має чутливий елемент з органічної плівки, яка розтягується при підвищенні вологості і стискується при пониженні. Зміна положення центра плівкової мембрани передається стрілці.

Волосяний і плівковий гігрометр у зимовий час є основними приладами для вимірювання вологості повітря. Їх покази періодично порівнюються з показами психрометра як більш точного приладу.

В електролітичному гігрометрі пластинку з електроізоляційного матеріалу (скло, полістирол) покривають гігроскопічним шаром електроліту – хлористого літію – зі зв’язувальним матеріалом. Зміна вологості повітря впливає на концентрацію електроліту і, як наслідок, його опір. Недоліком цього гігрометра є залежність його показів від температури.

Дія керамічного гігрометра базується на залежності електричного опору твердої і пористої керамічної маси (суміш глини, кремнію, каоліну і деяких окислів металів) від вологості повітря.

Конденсаційний гігрометр визначає точку роси за температурою металевого дзеркальця в момент появи на ньому при його охолодженні слідів води (чи льоду), сконденсованої з навколишнього повітря. Такий гігрометр складається з пристрою для охолодження дзеркальця, оптичного чи електричного пристрою, який фіксує момент конденсації, і термометра, який вимірює температуру дзеркальця. У сучасних конденсаційних гігрометрах для охолодження дзеркальця використовують напівпровідниковий елемент з ефектом Пельтьє, а температуру дзеркальця вимірюють вмонтованим в нього дротяним опором чи напівпровідниковим мікротермометром.

Все більше поширення знаходять електролітичні гігрометри з підігрівом, дія яких базується на принципі вимірювання точки роси над насиченим соляним розчином (зазвичай хлористим літієм), яка для даної солі має відому залежність від вологості. Чутливий елемент складається з термометра опору, на корпус якого обгорнутий скловолокном, просякнутим розчином хлористого літію, і двох платинових електродів, намотаних поверх скловолокна, на які подають змінну напругу.

Плавлення – це процес перетворення речовини з твердого стану в рідину. Кристалічні тіла мають певну температуру плавлення і кристалізації.

Процес плавлення супроводжується поглинанням теплоти, що витрачається на руйнування зв’язків у кристалічній решітці. Для плавлення кристалічного тіла масою m потрібно затратити кількість теплоти:

, (7.3)

де λ – питома теплота плавлення, тобто кількість теплоти, необхідна для перетворення 1кг речовини, взятої при температурі плавлення, у рідину з тією самою температурою, у СІ [λ] = Дж/кг.

Вже йшла мова про те, що одним з напрямків досліджень молекулярної фізики є вивчення так званих явищ переносу. Під явищем переносу у фізиці розуміють явища дифузії, в’язкості, теплопровідності, конвекції, електро-провідності, дифузії та інші, при яких відбувається перенесення енергії чи речовини. Розглянемо деякі з них.

Дифузія – це процес випадкового невпорядкованого переміщення частинок під впливом хаотичних сил, зумовлених тепловим рухом і взаємодією з іншими частинками.

Дифузія є перенесенням речовини, зумовленим вирівнюванням її концентрації (точніше, хімічного потенціалу) у спочатку неоднорідній системі. Це одна зі стадій численних технологічних процесів (адсорбції, сушки, екстрагування, брикетування зі зв’язуючими тощо). Дифузія відбувається в газах, рідинах і твердих тілах. Механізм дифузії в цих речовинах істотно різний. Дифузія що відбувається внаслідок теплового руху атомів, молекул, – молекулярна дифузія. Дифундувати можуть як частинки сторонніх речовин (домішок), нерівномірно розподілених у середовищі, так і частинки самої речовини середовища. У останньому випадку процес називається самодифузією. Термодифузія – це дифузія під дією градієнта температури в об’ємі тіла, бародифузія – під дією градієнта тиску або гравітаційного поля. Перенесення заряджених частинок під дією зовнішнього електричного поля називають електродифузією. У рухомому середовищі може виникати конвекційна дифузія, при вихровому русі газу або рідини – турбулентна дифузія.

Наслідком дифузії є переміщення часток з областей, де їхня концентрація висока, в області з низькою концентрацією, тобто вирівнювання концентрації часток у термодинамічній системі, встановлення рівноваги за складом.

Дифузія дуже розповсюджене явище, яке відіграє велику роль у функціонуванні живих організмів. У легенях кисень дифундує у кровоносні судини, завдяки процесам дифузії відбувається обмін речовин у клітинах.

Мірою дифузії є маса ΔМ речовини, що продифундувала за одиницю часу через одиницю площі поверхні контактних речовин. Для опису процесу вирівнювання концентрації часток в термодинамічній системі використовується рівняння дифузії. В загальному випадку воно є наслідком рівняння неперервності, яке визначає закон збереження кількості часток:

, (7.4)

де n – концентрація часток, j – їхній потік, .

В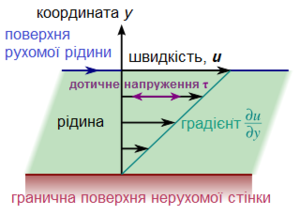 ’язкість або внутрішнє тертя – властивість текучих тіл (рідин і газів) чинити опір переміщенню однієї їх частини відносно іншої. Одиниця вимірювання – пуаз.

В’язкість рідин – це результат взаємодії внутрішньо-молекулярних силових полів, що перешкоджають відносному рухові двох шарів рідини. Отже, для переміщення шару один відносно одного треба подолати їх взаємне притягання, причому чим воно більше, тим більша потрібна сила зсуву. При відносному зсуві шарів у газовому середовищі, в результаті перенесення молекулами газу кількості руху під час їх переходу з шару в шар, виникає дотична сила між шарами, що протидіє проковзуванню останніх.

Таким чином, внутрішнє тертя в рідині, на відміну від газів, зумовлене не обміном молекул, а їх взаємним притяганням. Доказом цього є те, що із збільшенням температури, як відомо, обмін молекул зростає і тертя в газах зростає, а в рідинах спадає у зв'язку із послабленням міжмолекулярного притягання.

В’язкість твердих тіл має низку специфічних особливостей і зазвичай розглядається окремо.

Теплопровідність – здатність речовини переносити теплову енергію, а також кількісна оцінка цієї здатності: фізична величина, що характеризує інтенсивність теплообміну в речовині, яка дорівнює відношенню густини теплового потоку до градієнта температури.

Явище теплопровідності полягає в тому, що кінетична енергія атомів і молекул, яка визначає температуру тіла, передається атомам і молекулам у тих областях тіла, де температура нижча.

Теплопровідність не єдиний шлях, яким тепло передається від тіла з вищою температурою, до тіла з нижчою температурою. Така теплопередача може також відбуватися за рахунок теплового випромінювання і конвекції. Різниця між теплопровідністю й конвекцією в тому, що при конвекції тепло переноситься разом із речовиною, а при теплопровідності переносу речовини немає.

Найбільшу теплопровідність мають речовини, в яких тепло переноситься вільними електронами, що зумовлено їхньою малою масою. Саме тому теплопровідність металів зазвичай висока. В нагрітій області речовини є більше електронів із високою енергією, вони легко мігрують в холодніші області, й втрачають там енергію, розсіюючись на коливаннях кристалічної гратки. Діелектрики, наприклад, кераміка, мають меншу теплопровідність, що робить їх зручними для виготовлення посуду. В діелектриках, де немає вільних електронів, тепло передається повільнішими коливаннями атомів. Гази, наприклад, повітря, мають малу теплопровідність, зважаючи на невелику густину молекул і доволі нечасті зіткнення між ними. В газах тепло швидше переноситься через конвекцію.

З огляду на це, добрими теплоізоляційними властивостями характеризуються матеріали, в яких багато порожнин, заповнених повітрям: вовна, вата, пінопласт тощо (див. таблицю).

Матеріал	Теплопровідність, Вт/(м.К)	Матеріал	Теплопровідність, Вт/(м.К)
Алмаз	1000-2600	Платина	70
Срібло	430	Кварц	8
Мідь	390	Скло	1
Золото	320	Вода	0,6
Алюміній	236	Вовна	0,05
Латунь	111	Повітря	0,026

Поверхневий натяг – фізичне явище, суть якого полягає в прагненні рідини скоротити площу своєї поверхні при незмінному об’ємі. Характеризується коефіцієнтом поверхневого натягу.

Поверхневий натяг виникає як у випадку поверхні розділу між рідиною й газом, так і у випадку поверхні розділу двох різних рідин. Своєю появою сили поверхневого натягу завдячують поверхневій енергії⁷.

З авдяки силам поверхневого натягу краплі рідини приймають максимально близьку до сферичної форми, виникає капілярний ефект, у природі деякі комахи можуть ходити по воді.

Для зменшення сил поверхневого натягу використовуються поверхнево-активні речовини.

Наведемо деякі значення поверхневого натягу різних рідких середовищ:

Рідина	Поверхневий натяг, дин/см при 20С	Рідина	Поверхневий натяг, дин/см при 20С
Етиловий ефір	16,9	Анілін	42,9
Етиловий спирт	22,8	Сірчана кислота (85%)	57,4
Ацетон	23,7	Азотна кислота (70%)	59,4
Нафта	26	Гліцерин	59,4
Оцтова кислота	27,8	Вода	72,9
Бензол	29	Ртуть	465

Є два методи описування і дослідження процесів, які відбуваються в макроскопічних тілах: статистичний і термодинамічний.

Статистичний метод вивчення фізичних явищ ґрунтується на моделюванні внутрішньої структури речовини. Середовище розглядають як деяку фізичну систему, що складається з великого числа молекул (атомів) із заданими властивостями. Визначення макроскопічних характеристик і закономірностей за заданими мікроскопічними властивостями середовища є основним завданням цього методу. Його ще називають молекулярно-кінетичним.

Так, для сукупності молекул, що рухаються хаотично, можна знайти певні значення швидкості, енергії, імпульсу, які властиві більшості молекул. Такі значення величин називають найбільш ймовірними. Можна визначити середні значення швидкості молекул, їхні енергії, вільного пробігу молекул та ін., які є характеристиками руху сукупності молекул. За ними можна визначити такі параметри макроскопічної системи, як тиск, абсолютна температура тощо.

Статистичний метод дає змогу в уявному хаосі випадкових явищ встановлювати закономірності, які справджуються для цілого ансамблю явищ, а не для кожного елемента окремо, як у динамічній закономірності. Встановлені так взаємозв’язки називають статистичними закономірностями.

Ці закономірності втрачають зміст із переходом до систем із малим числом частинок.

Метод описування процесу, який розглядає речовину як суцільне середовище, називають термодинамічним.

Цей метод дає змогу встановити загальні співвідношення між параметрами, що характеризують явища загалом. Область застосування термодинаміки значно ширша, оскільки немає таких розділів фізики чи хімії, де не можна було б застосувати термодинамічний метод. Однак, з іншого боку, термодинамічний метод дещо обмежений: термодинаміка нічого не говорить про мікроскопічну будову речовини, про механізм явища, а лише встановлює зв’язки між макроскопічними властивостями речовини.

Розглядаючи властивості тіл та їхні зміни з двох різних позицій – мікроскопічної і макроскопічної, молекулярна фізика і термодинаміка доповнюють одна одну.

Тема №8. «Механіка рідин та газів»

1. Поняття гідроаеромеханіки.

2. Гідростатика та аеростатика.

3. Гідродинаміка та аеродинаміка.

4. Закон Паскаля. Рівняння неперервності.

5. Рівняння Бернуллі.

6. В’язкість. Формула Ньютона.

7. Рух тіл у рідинах або газах. Формула Стокса.

8. Ламінарний та турбулентний потоки.

9. Число Рейнольдса.

Гідроаеромеханіка – це розділ механіки, пов’язаний з вивченням рівноваги й руху рідинних і газоподібних середовищ, а також їхньої взаємодії між собою і з твердими тілами. Інші назви, що застосовують до цього розділу науки – механіка рідин та газів, гідрогазодинаміка або гідрогазомеханіка.

Сучасна гідроаеромеханіка базується на досягненнях гідромеханіки, розвиток якої йшов двома різними шляхами: теоретичним (теоретична гідромеханіка, що за своїм змістом та методами вивчення є складовою частиною теоретичної механіки) і експериментальним (гідравліка – стародавня наука про течію води). Гідроаеромеханіка, у свою чергу, дала початок самостійним напрямкам таким як газодинаміка, аеродинаміка, технічна гідромеханіка та ін.

Найголовнішим завданням гідроаеромеханіки як науки є встановлення законів розподілу швидкостей і тисків під час руху рідини, а також вивчення силової взаємодії між рідиною і твердими тілами, розміщеними у ній.

Гідрогазомеханіка є невід’ємною частиною комплексу технічних наук, необхідних для підготовки сучасного інженера. Практично усі галузі народного господарства включають питання теоретичної гідромеханіки, експлуатації гідроустаткування та технологій у процесах яких беруть участь рідини та гази. Гідроаеромеханіка займає одне з провідних місць при підготовці інженерів, що працюють в атомній енергетиці, авіації, суднобудуванні, промисловій теплоенергетиці, гідроенергетиці, будівництві гідроспоруд та ін.

Уже у стародавньому світі було накопичено багато спостережень та винайдено цікаві гідравлічні та пневматичні пристрої. Окремі спостереження були викладені у працях давньогрецького філософа Аристотеля (IV ст. до н.е.). Частину законів гідростатики сформулював великий математик та механік Стародавньої Греції Архімед.

Великий вклад у розвиток основ гідромеханіки зроблено Леонардо да Вінчі (1452-1519), Галілеєм (1564-1642), Паскалем (1623-1662), Гюйгенcом (1629-1695), Ньютоном (1642-1727).

М.В.Ломоносов (1711-1765), працюючи в галузі металургії, гірничої справи, водяних двигунів та метеорології вніс великий вклад у гідромеханіку. Л.Ейлером (1707-1783) було виведено рівняння рівноваги і руху рідин та газів, отримано деякі їх інтеграли та сформульовано закон збереження маси щодо рідини. Л.Ейлер вивів основне рівняння лопатевих гідромашин, дослідив питання руху стосовно практичних задач суднобудування та конструювання гідравлічних машин. Д.Бернуллі (1700-1782) вперше увів термін «Гідромеханіка». Він встановив залежність між питомими енергіями при русі рідини, дослідив тиск струменя рідини на пластину. Подією в історії розвитку гідротехніки став випуск його книги «Гідродинаміка або Записки про сили і рух в рідинах».

Подальший етап розвитку гідромеханіки, що об’єднав кінець ХVIII і початок XIX століть, характерний математичною розробкою гідродинаміки ідеальної рідини. У цей період вийшли праці математиків Лагранжа (1736-1813), Коші (1789-1857), присвячені потенціальним потокам, теорії хвиль та ін. Основи теорії в’язкої рідини були закладені Нав’є (1785-1836) та Стоксом (1819-1903). У 1881 р. професор Казанського університету І.С.Громеко (1851-1889) дав нову форму рівнянь руху рідини, зручну для отримання енергетичних залежностей. Ним же були вперше проведені дослідження нестаціонарного руху рідини в капілярах. І.Пулюй (1845-1918) у 1876 р. захистив докторську дисертацію «Залежність внутрішнього тертя газів від температури», у якій він опублікував результати досліджень температурної залежності в’язкості газів.

Англійський фізик О.Рейнольдс у своїх дослідах (1842-1912) встановив закон подібності потоків у трубах. Цілу епоху складають дослідження з повітроплавання, що включає розробку теорії польоту літака та ракети. Результати цих та інших досліджень були викладені в працях вчених Д.І.Менделєєва (1834-1907), М.Є.Жуковського (1849-1912), С.Д.Чаплигіна (1869-1942). Розроблена М.Є.Жуковським теорія крила і повітряного гвинта мала значення не тільки для авіації, але й для сучасного турбомашино-будування. Жуковський М.Є. в тогочасній Росії, як Ейфель (1832-1923) у Франції, Людвіґ Прандтль (1875-1950) в Німеччині, був творцем експериментальної аеромеханіки. Він створив відомий у всьому світі аерогідродинамічний інститут ЦАГІ. Великий внесок в теорію реактивного руху зробив К.Ціолковський (1857-1935).

Сучасний етап розвитку гідромеханіки характеризується появою її нових розділів: фізико-хімічної гідромеханіки, електромагнітної гідромеханіки, пов’язаних з багатьма новими галузями техніки. Механіка рідини у багатьох випадках важко піддається математичному опису. Ця проблема розв’язується за допомогою числових методів з використанням комп’ютерів. Сучасний розділ, що отримав назву обчислювальної гідродинаміки, присвячений розв’язанню задач механіки рідин. Розвиваються також технології візуалізації характеру протікання рідини математичного моделювання, а також експериментальні методи візуалізації та аналізу потоку рідини.

Основними розділами гідроаеромеханіки є: гідростатика, що вивчає рідину, яка перебуває у стані абсолютного чи відносного спокою, коли відсутні переміщення часток одна відносно одної; кінематика рідини, яка вивчає рух рідини без урахування діючих сил. Така властивість рідин і газів, як текучість створює додаткові ступені свободи, а розподіл тиску стає складнішим, ніж розподіл напружень у твердих тілах. Тому вивчення руху рідини і газу набагато складніше за вивчення руху твердих тіл теоретичною механікою чи вивчення їх деформацій в механіці деформованого твердого тіла; прикладна гідродинаміка рідини — розділ, що, ґрунтуючись на основах теоретичної гідромеханіки вивчає рух рідини з урахуванням діючих на неї сил для типових інженерних задач.

Як у будь-якій математичній моделі реального світу, у гідроаеромеханіці роблять деякі припущення про властивості матеріалу, що вивчається. Ці припущення перетворюються у рівняння, що завжди повинні виконуватись. Наприклад, розглянемо нестисливу рідину у трьох вимірах. Припущення, що маса зберігається, означає, що для будь-якої фіксованої замкнутої поверхні (наприклад, сфери) швидкість масового переходу ззовні до середини повинна бути такою ж, як швидкість масового проходження в інший бік. Крім того, маса всередині залишається незмінною, так само як і маса зовні.

Механіка рідини передбачає, що всі рідини підпорядковується таким законам та гіпотезам:

• закону збереження маси;

• закону збереження енергії;

• закону збереження імпульсу;

• гіпотезі про суцільність середовища⁸.

Параметри, що характеризують термодинамічний стан, спокій чи рух середовища, вважаються при цьому нерозривно змінними по всьому об’єму, зайнятому середовищем.

Крім того, часто буває корисно (для дозвукових швидкостей) вважати рідину нестисливою – тобто густина рідини не змінюється. Рідини часто можуть бути змодельовані як нестискувані рідини, чого не можна сказати про гази.

У гідроаеромеханіці зустрічається низка задач, в яких можна знехтувати і в’язкістю, приймаючи, що дотичні напруження відсутні так, як це має місце у рідині, що перебуває у стані спокою. Гази часто можна вважати нев’язкими. Якщо рідина в’язка і її потік, що міститься в деякому руслі (наприклад, у трубі), то потік на стінці повинен мати нульову швидкість. Це явище називається прилипанням.

Описана вище гіпотетична рідина з переліченими властивостями, а саме:

• абсолютною незмінністю об’єму;

• повною відсутністю в’язкості

називається ідеальною рідиною.

Поняття ідеальної рідини вперше було введено Л.Ейлером. Така рідина є граничною абстрактною моделлю, і лише наближено відображає об’єктивно наявні властивості реальних рідин. Однак, ця модель дає змогу з достатньою точністю розв’язувати багато дуже важливих питань гідрогазодинаміки й сприяє спрощенню складних задач.

Отже, гідростатика – це розділ гідромеханіки, що вивчає закони рівноваги рідини, які перебуває у стані абсолютного чи відносного спокою та рівноваги тіл, занурених у рідину за умови, коли відсутні переміщення часток рідини одна відносно одної.

Рідина, що перебуває у стані спокою у системі координат, зв’язаній із Землею, знаходиться в абсолютному спокої. Спокій рідини у системі координат, котра рухається відносно Землі, називають відносним.

У загальному випадку рідина зазнає дії масових і поверхневих сил. При цьому спокій рідини спостерігається тільки у випадку, коли масові сили мають потенціал і постійні у часі. Зазвичай, розглядають стан спокою рідини, що піддається дії сил гравітації та інерції.

Рідина, на відміну від твердих тіл, має властивість текучості, саме тому в рідині не може існувати анізотропії напружень, а значить замість багатокомпонентного тензора напруження в рідині описується скалярною величиною – тиском.

Основним завданням гідростатики є визначення (опис) скалярного поля тиску у рідині, що перебуває у спокої. Цей тиск описується рівнянням:

(8.1)

де: – векторне поле одиничних масових сил (сила, що діє на одиницю маси рідини); ρ– густина рідини; p – тиск.

Це співвідношення може бути отримане з рівняння Нав'є-Стокса, за умови, що швидкість дорівнює нулю. Воно справедливе як для нестисливої (ідеальної) рідини, так і для стисливої (реальної) рідини та газів.

За відсутності масових сил ( ) рівняння спрощується до вигляду:

. (8.2)

Це означає, що коли у рідині масові сили відсутні, тиск в рідині рівномірно розподіляється у всіх точках рідини. Цю закономірність, вперше сформулював Паскаль, звідси і назва «закон Паскаля», що традиційно вважається найважливішим законом гідростатики.

Коли масова сила рівномірно розподілена по всьому об'єму рідини і спрямована вздовж осі, тиск залежить лише від цієї координати, і рівняння рівноваги рідини може бути зведене до вигляду:

(8.3)

або

, (8.4)

де: F_z – одинична сила у напрямку осі z; dz – приріст координати положення; dp – відповідний приріст тиску.

Коли густина рідини не залежить від тиску, що практично справедливе для всіх рідин, і одинична масова сила відповідає прискоренню вільного падіння F_z = g, рівняння, що описують тиск рідини записується як:

, (8.5)

де: р – тиск у рідині на глибині H; р₀ – тиск, що діє на поверхню рідини.

Це основне рівняння гідростатики показує, що абсолютний гідростатичний тиск в будь-якій точці простору, зайнятому рідиною, дорівнює сумі зовнішнього тиску p₀ і надлишкового тиску ρgH.

З цього рівняння випливає рівність рівнів у сполучених посудинах, пояснення гідростатичного парадоксу та закону Архімеда.

Гідростатичний парадокс (парадокс Паскаля) – явище непропорційності тиску на дно посудини вазі налитої в неї рідини. Парадоксальність явища полягає у тому, що вага налитої у посудину рідини може відрізнятися від сили її тиску на дно цієї посудини. Першим на цей факт, що на той час видався парадоксальним, вказав фламандський математик Сімон Стевін (1548-1620).

Друга назва цього парадоксу – «парадокс Паскаля», котрий спопуляризував це явище своїми дослідами. Він продемонстрував цей парадокс у 1648. Паскаль вставив в закриту бочку, наповнену водою, тонку трубку і, піднявшись на балкон другого поверху, влив в цю трубку кухоль води. Через малий діаметр трубки вода в ній піднялася до великої висоти, і тиск в бочці збільшився настільки, що кріплення бочки не витримали, і вона почала пропускати воду через щілини.

Ц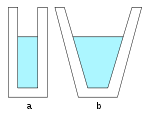 е явище пояснюється основним рівнянням гідростатики, згідно з яким тиск залежить від глибини занурення (висоти стовпа рідини), але не залежить від її кількості у посудині та форми посудини. Якщо вважати, що g і  є сталими в усіх точках рідини, то зміна тиску в залежності від глибини буде мати лінійний характер і описується рівнянням:

. (8.6)

Цим же виразом пояснюється рівність тисків на дно посудин різної форми при однаковій глибині.

У газах, в тому числі і в земній атмосфері (повітрі), густина суттєво залежить від тиску і ця залежність описується рівнянням стану ідеального газу:

, (8.7)

де:  – молярна маса газу, R – універсальна газова стала, T – температура газу.

Звідси випливає залежність тиску газу від висоти (барометрична формула):

. (8.8)

Закон гідростатики: на будь-яке тіло, занурене в рідину або газ, діє виштовхувальна сила, яка дорівнює вазі витисненої даним тілом рідини (газу), за напрямом протилежна їй і прикладена у центрі мас витісненого об’єму рідини.

Основна теорема гідростатики сформульована і доведена Л.Ейлером у 1755 році. У ній говориться, що величина гідростатичного тиску в даній точці не залежить від орієнтації в просторі площини, на якій вона розташована.

З акон Паскаля стверджує, що тиск, прикладений ззовні до рідини або газу у закритій посудині передається у всі точки середовища однаково. Таким чином, рідина має властивість передавати зовнішній тиск усім розташованої всередині неї частинкам рідини без зміни.

Аеростатика (від грец. Αερ – повітря; στατός – «нерухомий») – це розділ гідроаеромеханіки, в якому вивчається рівновага газоподібних середовищ, в основному атмосфери.

Головним представником газоподібних речовин є атмосферне повітря. Повітря, як і рідкі та тверді тіла, перебуває під впливом сили тяжіння, і через це тисне на поверхню Землі. На противагу силі тяжіння повітря має особливе прагнення, характерне для всіх газів, розширитися й зайняти якнайбільший об’єм, тобто, повітря володіє пружністю. Ця властивість є причиною зменшення густини атмосферного повітря у верхніх шарах, оскільки силі розширення, чи пружності шару повітря, яке знаходиться на великих висотах, протидіє відносно менший тиск решти шарів, які знаходяться вище.

Наслідком легкої рухливості частинок повітря є той факт, що будь-який тиск на повітряну масу передається і поширюється рівномірно у всі боки. Можна прийняти в середньому, що повітря тисне на будь-яку площу земної поверхні як стовп ртуті з тією ж основою висотою 760 мм, або як стовп води висотою 10,4 м. Це створює в середньому тиск 1 кг на квадратний сантиметр, що прийнято вважати одиницею тиску, тобто, пружності парів.

Прилади, призначені для вимірювання тиску, називаються манометрами. За призначеннями манометри бувають:

• для вимірювання абсолютного тиску, відлік якого починають від нуля (абсолютного вакууму);

• для вимірювання надлишкового тиску, тобто різниці між атмосферним і абсолютним тиском, більшим від атмосферного;

• для вимірювання різниці двох тисків, відмінних від атмосферного (дифманометри);

• для вимірювання тиску розріджених газів (вакуумметри);

• для вимірювання атмосферного тиску (барометри).

Дослідами встановлено, що об’єм відомої повітряної маси змінюється обернено пропорційно до його пружності, тобто тиску, який на нього діє.

У аеродинаміці розглядають рух з дозвуковими швидкостями, тобто в нормальних умовах до 340 м/с (1200 км/год). Аеродинаміка розв’язує такі прикладні задачі:

• розподіл тиску по поверхні тіла;

• визначення сил і моментів, що діють на тіло, яке обтікає газ;

• розподіл швидкостей у повітряному потоці, що обтікає тіло;

• розрахунок вентиляції;

• розрахунок пневмотранспорту.

Спеціальний розділ аеродинаміки – аеродинаміка літаків – займається розробкою методів аеродинамічного розрахунку і визначенням аеродинамічним сил і моментів, які діють на літак в цілому і на його частини (крило, фюзеляж та ін.) зокрема. До аеродинаміки літака належать: розрахунок стійкості, балансування літака, теорію повітряних гвинтів, теорію крила.

Закони аеродинаміки враховуються в літакобудуванні, авіабудуванні, автомобілебудуванні, в різноманітних літальних апаратах.

У подальшому розвитку аеродинаміки, при вивченні умов, які суттєво відрізняються від нормальних, виникла газова динаміка. Особливістю, що відрізняє її від класичної аеродинаміки, є умови, при яких стискуваність газів стає суттєвим фактором, який впливає на рівняння стану і, відповідно, поведінку. У першу чергу, це швидкості газових потоків, близькі чи більші від швидкості звуку в газі, що призводить до появи значних перепадів тиску і ударних хвиль. Іншим прикладом є процеси в газових середовищах, які супроводжуються екзотермічними (горіння, вибух) чи ендотермічними (дисоціація) хімічними реакціями: у цих випадках через зміну середньої молекулярної маси газу і процесів енерговиділення модель ідеального газу неприйнятна.

Рівняння неперервності в гідродинаміці називають рівнянням нерозривності. Воно уособлює закон збереження маси в елементарному об’ємі, тобто безперервність потоку рідини чи газу. Його диференціальна форма має вигляд:

(8.9)

де  – щільність рідини (або газу),  – вектор швидкості рідини (або газу) в точці з координатами (x, y, z) в момент часу t.

Вектор називають щільністю потоку рідини. Його напрямок збігається з напрямком течії рідини, а абсолютна величина визначає кількість речовини, що протікає в одиницю часу через одиницю площі, розташовану перпендикулярно вектору швидкості.

Для нестискуваних рідин . Тому рівняння приймає вид

.

Рівняння Бернуллі – рівняння гідродинаміки, яке визначає зв’язок між швидкістю течії v, тиском p та висотою h певної точки в ідеальній рідині. Встановив його у 1738 році Даніель Бернуллі.

Для ламінарної течії ідеальної нестисливої рідини рівняння Бернуллі має вигляд:

(8.10)

або

. (8.11)

В останньому рівнянні всі члени мають розмірність тиску: p – статичний тиск; – динамічний тиск; hρg – ваговий тиск.

Якщо такі рівняння записати для двох перерізів течії, то матимемо:

. (8.12)

Для горизонтальної течії середні члени у лівій і правій частині рівняння скорочуються і воно набуває вигляду:

, (8.13)

тобто в стаціонарній горизонтальній течії ідеальної нестисливої рідини в кожному її перерізі сума статичного і динамічного тисків буде сталою. Отже, в тих місцях течії, де швидкість рідини більша (вузькі перерізи), її динамічний тиск збільшується, а статичний зменшується. На цьому явищі заснована дія струминних насосів, ежекторів, витратомірів Вентурі й Піко, пульверизаторів.

Рівняння Бернуллі є наслідком закону збереження енергії. Якщо рідина не ідеальна, то її механічна енергія розсіюється і тиск вздовж трубопроводу, яким тече така рідина, спадає. Для реальної в’язкої рідини в правій частині рівнянь, слід додати величину втрат тиску Δр_вт на гідравлічний опір рухові.

Рівняння Бернуллі широко застосовують для розв’язання багатьох гідравлічних задач у нафтогазовій справі.

Донедавна закон Бернуллі застосовували для пояснення причини підіймальної сили крила. Відповідно до цього закону, пояснення підіймальної сили літака виглядає так: крило має особливу будову – знизу воно пряме, а його верхня частина заокруглена. Це дозволяє збільшити площу верхньої частини крила. Згідно із законом Бернуллі, зі збільшенням швидкості тиск зменшується. А оскільки повітря долає шлях під крилом та над крилом за однаковий проміжок часу, під крилом виникає область підвищеного тиску, що зумовлює підйом літака у повітря. Так виникає підйомна сила.

Проте, згідно з сучасними уявленнями, підіймальна сила крила виникає не внаслідок закону Бернуллі. Рух повітряної маси перед крилом можна вважати суцільним, він характеризується одним показником швидкості. Коли повітряна маса контактує з крилом, вона розбивається на дві частини, які, внаслідок форми крила, мають різні швидкості і це зумовлює різний тиск. Однак це не може бути причиною підйомної сили, оскільки ці дві повітряні маси обтікають відповідно верхню і нижню частини крила не за однаковий час, бо, на відміну від колишніх уявлень, ці повітряні потоки не поєднуються на кінці крила. Тобто, більша довжина верхньої частини крила не означає більшої швидкості руху повітря. Отже, хоча закон Бернуллі й можна застосувати для повітряних мас, які розсікаються крилом (більша швидкість зумовлює менший тиск), проте він один не пояснює підіймальну силу крила. Для повного пояснення слід застосовувати теорему Жуковського:

, (8.14)

де Y – підйомна сила, ρ – густина повітря, v – швидкість руху незбуреного потоку, Г – циркуляція швидкості, яку обчислюють за формулою (dА – елемент контура). Частина аеродинаміки, що пояснює рух стисливої рідини (газу), називається газовою динамікою.

У пульверизаторі застосовується головний наслідок закону Бернуллі: зі зростанням швидкості відбувається зростання динамічного тиску та спадання статичного тиску. У капіляри пульверизатора вдувається повітря або пара. Вдування знижує атмосферний тиск у капілярі, і рідина з балону пульверизатора під дією більшого атмосферного тиску піднімається капіляром. Там вона роздроблюється струменем повітря.

Водоструминний насос – резервуар, у який впаяні дві трубки. Під дією тиску у першу трубку протікає вода, потрапляючи потім у другу трубку. У звуженій частині першої трубки виникає зменшений тиск, який менший за атмосферний. Тому у резервуарі створюється напруження. Трубку приєднують до резервуару, який проходить у посудину, з якої необхідно відкачати повітря.

Карбюратор – пристрій у системі живлення карбюраторних двигунів внутрішнього згоряння, що застосовується для змішування бензину та повітря. Під час руху поршня у такті впускання тиск у циліндрі знижується. При цьому навколишнє повітря всмоктується циліндром через повітряну трубу карбюратора – дифузор. У найвужчій частині дифузора, де тиск відповідно найменший, розташовано розпилювач, із якого витікає паливо. Паливо подрібнюється струменем повітря на маленькі краплі, і утворюється горюча суміш.

Осушування боліт за принципом закону Бернуллі проводилося дуже давно. До болота підводили канали від найближчої річки. Внаслідок великої різниці тисків між водою з болота та водою з каналу вода з каналу «всмоктувала» воду з болота.

У конструюванні ракет також застосовується закон Бернуллі. Для створення тяги у ракеті використовується паливо, яке спалюють у камері згоряння. Гази утворюють реактивний струмінь, який прискорюється, коли проходить через спеціальне звуження – сопло. Саме звуження сопла і є основною причиною прискорення реактивного струменя газів і збільшення реактивної тяги.

Свисток являє собою приклад використання закону Бернуллі у газо-струменевих випромінювачах звукових хвиль. Вихровий свисток являє собою циліндричну камеру, у подається потік повітря через тангенціально розташовану трубку. Утворений вихровий потік надходить у вихідну трубку меншого діаметру, яка розташована на осі. Там інтенсивність вихору різко підвищується та тиск в його центрі стає значно нижче атмосферного. Перепад тиску періодично вирівнюється за рахунок прориву газів з атмосфери у вихідну трубку та руйнування вихору.

Диск Релея – прилад для вимірювання коливальної швидкості частинок у звуковій хвилі та сили звуку. Являє собою тонку пластинку круглої форми, із слюди або металу, підвішену на тонку кварцову нитку. Зазвичай диск розміщують під кутом у 45º до напряму коливань частинок середовища, оскільки таке розташування є найчутливішим до коливань. При розповсюдженні звукових хвиль диск повертається перпендикулярно до напряму коливань. Це відбувається через те, що при обтіканні пластинки тиск, згідно із законом Б ернуллі більший у тому місці, де швидкість менша. Сили тиску утворюють обертальний момент, який урівноважується за рахунок пружності нитки. При цьому диск встановлюється до напряму потоку під кутом, що більший, ніж 45º. За кутом повороту диска визначають силу звуку. У постійному потоці кут повороту диска Релея пропорційний квадрату швидкості, при звукових коливаннях – квадрату амплітуди швидкості, і цей кут не залежить від частоти.

Згідно із законом Ньютона для внутрішнього тертя в’язкість характеризується коефіцієнтом пропорційності η між напруженням зсуву і градієнтом швидкості руху шарів у перпендикулярному до деформації зсуву напрямку (поверхні шарів):

. (8.15)

Коефіцієнт η називають коефіцієнтом динамічної в’язкості, динамічною в’язкістю або абсолютною в’язкістю. Одиниця вимірювання коефіцієнта динамічної в’язкості – Па c, Пуаз (0,1Па·с).

Кількісно коефіцієнт динамічної в'язкості дорівнює силі F, яку треба прикласти до одиниці площі зсувної поверхні шару S, щоб підтримати в цьому шарі ламінарну течію зі сталою одиничною швидкістю відносного зсуву.

Закон Ньютона для в’язкості, наведений вище, є класичною моделлю в’язкості. Це не основний закон природи, а наближення, що має місце для деяких матеріалів і не підтверджується для інших. «Не-ньютонівські» рідини мають значно складніший зв’язок між напруженням зсуву і градієнтом швидкості, ніж проста лінійність. Тому, для різних видів рідин застосовують різні моделі в’язкості:

• Н 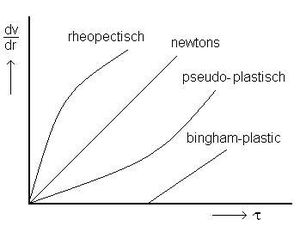ьютонівська рідина: рідина, така як вода і більшість газів, що має стале значення динамічної в’язкості.

• Дилатантна рідина: рідина, в’язкість якої зі зростанням градієнту швидкості зростає (глиняні суспензії, солодкі суміші, гідрозоль кукурудзяного крохмалю, системи пісок/вода).

• Псевдопластик: рідина, в’язкість якої зі зростанням градієнту швидкості зменшується (фарби, емульсії, деякі суспензії).

• Tиксотропна рідина: рідина, в’язкість якої з перебігом часу зменшується (водоносні ґрунти (пливуни), біологічні структури, різні технічні матеріали).

• Реопексна рідина: рідина, в'язкість якої з перебігом часу зростає (гіпсові пасти, суспензії оксиду ванадію, бетоніти та окремі види принтерного чорнила).

• Бінгамівський пластик: модель Бінгама, схожа до моделі сухого тертя. В статичних умовах рідина веде себе як твердий матеріал, а при силовому впливі починає текти.

• Магнітореологічна рідина – це тип «смарт-рідини», яка, при впливі магнітного поля значно збільшує свою умовну в’язкість і набуває властивостей в’язко-пружного твердого тіла.

В основу методів вимірювання в’язкості та їхньої класифікації покладено математичні залежності, які описують різні види течій середовищ. Вимірювання в’язкості здійснюють віскозиметрами.

Існує два режими течії рідини: ламінарний і турбулентний. При ламінарному режимі рідина рухається струминками або шарами без взаємного перемішування. При турбулентному режимі, навпаки, відбувається досить сильне перемішування частинок рідини.

Безрозмірне число Рейнольдса дозволяє судити про характер руху рідини

, (8.16)

де l – характерний лінійний розмір потоку, м; ν – кінематична в’язкість рідини, м/с².

Для труб круглого перерізу число Рейнольдса розраховують за формулою

, (8.17)

де d – діаметр труби, м.

Для всіх інших поперечних перерізів (а також для відкритих русел)

, (8.18)

або

, (8.19)

де d_e – еквівалентний (гідравлічний) діаметр, м,  .

Критерієм визначення режиму потоку є нерівність , де Re_кр – критичне значення числа Рейнольдса.

Критичним значенням числа Рейнольдса можна вважати: стосовно до формули (8.17) ; стосовно до формули (8.18) .

Якщо заміряти швидкість у турбулентному потоці в визначеній точці, то характер зміни швидкості в часі буде мати вигляд, близький до показаного на такому рисунку:

Складові швидкості турбулентного потоку. – усереднена в часі швидкість рідини; u – миттєве значення швидкості; – пульсаційна складова швидкості.

Для миттєвих значень складових швидкості і тиску мають місце співвідношення:

, (8.20)

де – інтеграл по достатньо великому проміжку часу від дійсного значення швидкості, тобто усереднена в часі складова дійсного значення швидкості вздовж осі х; – осі у; – осі z.

Тоді усереднені в часі значення пульсаційних величин будуть дорівнювати нулю

.

Пульсаційні складові швидкості, як і всі інші періодично змінні величини, можуть бути охарактеризовані частотою n і амплітудою А. Турбулентний рух має широкий діапазон величин А і n. В кожній точці турбулентного потоку мають місце пульсаційні швидкості з цілим спектром частот: низькі – 5...10 Гц, дуже високі – 50...100 Гц. Переважають завжди низькочастотні коливання.

Величина інтенсивності турбулентності змінюється від 0,3% в атмосфері до 7-8% і більше в машинах.

Природа дотичних напружень, які виникають в турбулентному потоці, більш складна, ніж в ламінарному. В процесі турбулентного перемішування маси рідини із центральної частини труби попадають в область потоку у стінок, і навпаки, частинки, які рухаються у стінок – в центральну область потоку. Маси, які переміщуються із центральної частини потоку до периферії, мають більші повздовжні швидкості, ніж ті, що переміщуються в протилежному напрямку, так як усереднена місцева швидкість більша в центральній області потоку. Маси, які рухаються з меншими швидкостями, коли попадають в область більших усереднених швидкостей, гальмують рух рідини в цій області. Отже, обмін масами рідини в потоці у поперечному напрямку призводить до відповідного обміну кількістю руху.

Для найпростішого випадку плоскопаралельного турбулентного потоку, який тече вздовж осі х, можна записати:

. (8.21)

Перший доданок відповідає в’язкісним дотичним напруженням, які визначаються за гіпотезою Ньютона, а друге τ₀ – турбулентним напруженням.

Якщо представити турбулентні напруження по аналогії з законом Ньютона

, (8.22)

то величину А в цій формулі можна розглядати як коефіцієнт «турбулентної в’язкості», викликаний макропереносом кількості руху скінчених об’ємів рідини поперечними пульсаціями швидкості. Якщо на випадок руху в плоскій труби припустити, що величина А постійна по перерізу, і визначити її по виміряному опору труби, то виявиться, що вона в десятки разів перебільшує величину коефіцієнта молекулярної в’язкості m.

Тема №9. «Електрика. Електростатика»

1. Порівняння електричної та гравітаційної взаємодій. Закон Кулона.

2. Електростатика. Закон збереження електростатичного заряду.

3. Електричне поле. Напруженість та потенціал поля.

4. Енергія електричного поля.

5. Теорема Гаусса, її застосування для розрахунку поля.

6. Електричне поле в діелектриках.

7. Поляризація діелектриків, діелектрична сприйнятливість та проникність речовини.

8. Умови на границі двох діелектриків. Електричне зміщення.

9. Типи діелектриків. Сегнетоелектрики.

Ще достатньо давно було відомо, що бурштин, потертий вовняною тканинкою, набуває здатності притягувати легкі предмети. Однак лише наприкінці XVI століття англійський лікар Джільберт детально дослідив це явище і відкрив подібну властивість в інших речовин. Такі тіла він назвав наелектризованими (від грецького ηλεκτρόν – бурштин). Тепер ми кажемо, що тіла в такому стані характеризуються електричним зарядом, і їх називають зарядженими.

В деяких тілах електричні заряди можуть вільно переміщуватися між різними частинами тіла, в інших такого бути не може. Тіла першого виду називають провідниками, тіла другого виду – діелектриками чи ізоляторами. Провідниками є всі метали в твердому чи рідкому стані, водні розчини солей і кислот, та багато інших речовин. Прикладами ізоляторів можуть слугувати бурштин, кварц, ебоніт і всі гази в нормальних умовах.

Одним з відомих проявів електромагнітної взаємодії є притягання й відштовхування заряджених тіл. У 1785 році Шарль Кулон ⁹ дослідним шляхом встановив закон взаємодії електричних зарядів

, (9.1)

д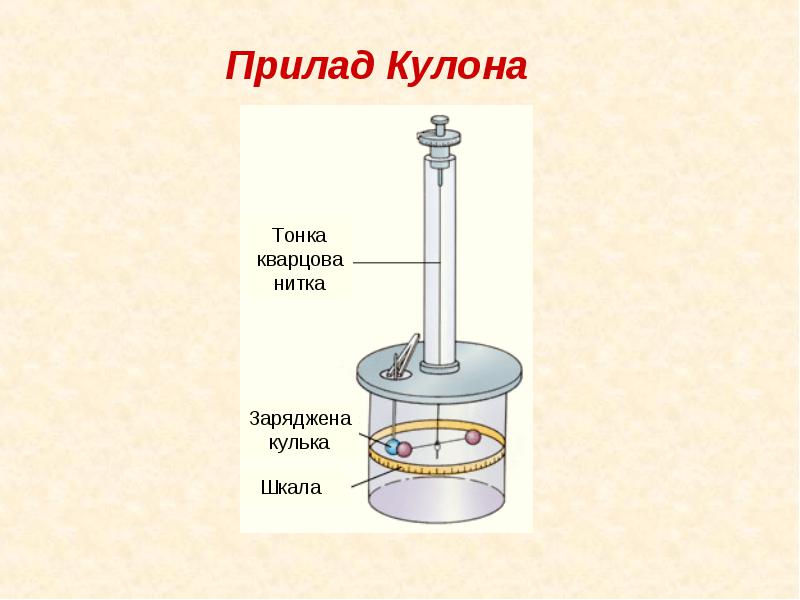 е k – коефіцієнт, що дорівнює 9^.10⁹ Н^.м²/Кл². Згідно з цим законом два електричних заряди q_t і q_r, що знаходяться на відстані r, притягаються (якщо вони різнойменні) або відштовхуються (якщо однойменні) з силою, обернено пропорційною до віддалі між зарядами.

Для заряджених тіл довільних розмірів такий закон в загальному вигляді подавати не можна, оскільки сила взаємодії розмірних тіл залежить від їх форми та взаємного розташування. Однак, якщо віддаль між тілами суттєво більша від їх розмірів, то форма й розміри тіл перестають відігравати роль. Тому закон взаємодії, що має загальне значення, можна встановити лише для точкових зарядів.

Досліди Кулона, звичайно, не є єдиним доказом справедливості закону (9.1). На сьогодні проведено багато інших експериментів, які демонструють виконання закону Кулона як на великих, так і на достатньо малих віддалях. Зокрема, дослідження атомних явищ дозволяють зробити висновок, що закон взаємодії електричних зарядів справедливий, по крайній мірі, до віддалей порядку 10^-15 м.

Досліди показують, що при електризації завжди виникають два типи зарядів, рівні за значенням, але протилежні за знаком. При терті електризуються обидва тіла однаково з точки зору величини заряду, але протилежними за знаком зарядами. Звідси й притягання між тілами. Такий ефект привів до висновку, що у всіх тілах є в наявності заряди обох знаків в рівних кількостях, що зумовлює електричну нейтральність тіл в звичайному стані. Заряджання тіл означає не виникнення зарядів, а їх перерозподіл між тілами (чи частинами тіл). Однак, алгебраїчна сума зарядів, що виникають в будь-якому електричному процесі, дорівнює нулю.

На сьогодні вже чітко встановлено, що носіями заряду є так звані елементарні частинки, які в межах класичної фізики прийнято вважати неподільними (звідси й назва «елементарні»). За одиницю вимірювання прийнято вважати заряд однієї негативно зарядженої частинки – електрона, рівний 1,6^.10^-19 Кл. Маса електрона надзвичайно мала і складає 10^-30 кг. Тому заряджання тіла практично не впливає на його масу.

Закон взаємодії електричних зарядів дуже схожий на закон гравітаційної взаємодії: там сила взаємного тяжіння тіл прямо пропорційна добутку їх мас і обернено пропорційна квадрату відстані між ними Обидві взаємодії, електромагнітна й гравітаційна, належать до числа далеко діючих. Вони виявляються на будь-якій відстані. Однак ці взаємодії дуже сильно розрізняються за своєю інтенсивністю.

Порівняємо, наприклад, силу гравітаційного притягання (F_гр) двох протонів, що знаходяться на відстані 2^.10^-13 см (на такій відстані вони розташовані в атомному ядрі) з силою їх електростатичного відштовхування (F_ел). Знаючи масу й електричний заряд протона, легко обчислити, що:

F_гр = 5^.10^-35Н, F_ел = 60H.

Тобто, електростатична взаємодія двох протонів приблизно в 10³⁶ разів сильніша, ніж їхня гравітаційна взаємодія, причому це співвідношення справедливе при будь-якій відстані між протонами. Якби ми для порівняння взяли не два протони, а протон з електроном, то розходження зросло б ще приблизно в 2000 разів, а якби взяли два електрони, то в 4^.10⁶ разів.

Чому ж, зіштовхуючись з електростатичною взаємодією в житті, ми не помічаємо цієї її величезної сили; навпаки, у нас складається враження, що електростатична взаємодія набагато слабша за гравітаційну?

Це пояснюється двома причинами. По-перше, гравітаційні ефекти, які ми спостерігаємо, визначаються величезною масою Землі. По-друге, у гравітаційній взаємодії беруть участь усі без винятку атоми всіх тіл, тобто усі нейтрони, усі протони й електрони, із яких ці атоми складаються. Між тим, у повсякденному житті ми ніколи не бачимо повного прояву електростатичних тіл. У макроскопічному шматку речовини майже всі позитивні й негативні заряди компенсують один одного, тому що вони зв’язані в електрично нейтральні системи – атоми. Ефект взаємодії наелектризованих тертям предметів, наприклад, зумовлений лише незначним надлишком (або нестачею) однойменного заряду в порівнянні із загальною кількістю зв’язаних зарядів у цих предметах. Ці невеликі надлишки зарядів і впливають на весь шматок речовини, наприклад надають йому прискорення. Зрозуміло, що через велику масу нейтральних атомів із взаємно компенсованими зарядами прискорення макротіла буде невеликим. Тільки в мікросвіті, де кожен заряд працює «винятково на себе» (тобто, на масу тієї елементарної частинки, з якою він зв’язаний електростатично), ці сили проявляються повною мірою. Цікаво, що якби предмети навколо нас складалися не з нейтральних атомів, а хоча б з однозарядних іонів (тобто, атомів, що мають один позитивний або негативний заряд), то електростатична взаємодія між ними була б надзвичайно великою. При цьому досить «перетворити» на однозарядні іони лише невелику частку атомів.

Наприклад, між двома макротілами існуватиме електромагнітна взаємодія, сила якої дорівнює силі їхньої гравітаційної взаємодії, якщо в них перетворити на іони всього 10^-18 частини атомів. У 1 см³ будь-якої твердої речовини міститься в середньому 5^.10²² атомів. З них треба іонізувати всього 5^.10⁴. Ця кількість міститься в кубику з ребром 0,01 мкм. Навіть якщо розподілити всі ці іони в одноатомному шарі (завтовшки 10⁸ см), то й тоді площа ділянки шару, зайнятого іонами, складе всього 10^-10 см², тобто 0,01 мкм². От яка мізерна кількість іонів може повністю компенсувати гравітацію!

Крім електростатичного притягання (або відштовхування) електричних зарядів за законом Кулона, існує ще багато видів електромагнітної взаємодії. Електромагнітна взаємодія, наприклад, визначає хімічні, пружні сили й сили тертя, випромінювання електромагнітних хвиль і багато чого іншого.

В електромагнітній взаємодії беруть участь всі елементарні частинки, крім нейтрино й антинейтрино. Навіть якщо частинка не має електричного заряду, вона все одно бере участь в електромагнітній взаємодії, тому що взаємодія електричних зарядів – це лише один із численних електромагнітних ефектів, що спостерігаються в природі.

Найменший час, за який мікрочастинки встигають провзаємодіяти електромагнітним способом, t_ел-маг ≈ 10^-20 с.

Одним з основних законів електростатики є закон збереження електростатичного заряду, згідно з яким в замкнутій системі сумарний електричних заряд залишається постійним:

. (9.2)

Електричне поле – це одна з двох складових електромагнітного поля, яка характеризується впливом на електрично заряджену частинку з силою, пропорційною заряду частинки, і незалежною від її швидкості.

Векторна фізична величина, яка дорівнює силі, що діє у даній точці простору у даний момент часу на одиничний електричний заряд у електричному полі, називається напруженістю електричного поля:

, (9.3)

де – сила, q – електричний заряд. В системі СІ вимірюється у В/м, на практиці здебільшого у В/см.

Для опису електричного поля потрібно задати вектор напруженості у кожній точці поля. Це можна зробити аналітично, виражаючи залежність напруженості від координати точки. Однак, таку залежність можна подати й графічно, використовуючи лінії напруженості електричного поля.

Л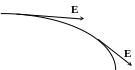 ініями напруженості електричного поля називають лінії, дотичні до яких напрямлені так само, як і вектор напруженості в даній точці поля (див. рисунок). Оскільки дотична, як і будь-яка пряма, визначає два взаємно протилежні напрямки, то лінії напруженості приписують певний напрям, який на рисунку позначають стрілкою.

Оскільки в кожній точці поля напруженість має строго визначене значення і напрям, лінії напруженості ніде не перетинаються. Вони починаються й закінчуються на тілах (предметах), на яких виникають індукційні заряди. Величину напруженості на схемах прийнято позначати за допомогою віддалі між лініями. Отже, маючи таку карту поля, можна завжди визначити величину й напрям напруженості в кожній його точці.

Потенціал електричного поля – енергетична характеристика електричного поля. Це скалярна величина, що дорівнює відношенню потенційної енергії заряду в полі до величини цього заряду. В системі СІ потенціал електричного поля вимірюється у вольтах.

У електростатиці електростатичний потенціал φ визначається згідно зі співвідношенням

, (9.4)

де – напруженість електричного поля.

Електростатичний потенціал визначають з точністю до довільної сталої. На практиці найчастіше за початок відліку служать потенціал заряду на нескінченості, або потенціал землі. В системі одиниць СІ й на практиці одиницею вимірювання потенціалу є вольти.

Точковий заряд q створює в точці спостереження r електричне поле з напруженістю

. (9.5)

Згідно з означенням електростатичного потенціалу

. (9.6)

В середовищі потенціал зменшується в ε разів, де ε – діелектрична стала¹⁰.

Матеріал	Діелектрична стала
Вакуум	1 (за визначенням)
Повітря	1,0005
Папір	3
Гума	7
Метиловий спирт	30
Вода	80
Титанат барію	1200

Електростатичний потенціал має властивість адитивності: потенціал системи зарядів дорівнює сумі потенціалів, створених кожним із них:

. (9.7)

На поверхні провідника електростатичний потенціал сталий, незалежно від форми провідника. Сталість потенціалу досягається перерозподілом зарядів. В такому випадку задачею електростатики є знаходження розподілу зарядів і водночас електростатичного потенціалу в просторі між цими зарядами, де потенціал задовольняє рівнянню Лапласа

. (9.8)

Якщо скористатись співвідношенням при , то маємо . Це означає, що всередині металів немає об’ємної густини заряду! Це не означає, що ніяких зарядів у металі немає. Просто позитивний і негативний заряд взаємно компенсують один одного. Розрахунки показали, що якщо виникне локальний об’ємний заряд внаслідок флуктуації, він буде скомпенсований за час с.

Що все це дає? Якщо вирізати порожнину у металі, розподіл полів не зміниться. На цьому принципі базується електростатичний захист чутливої апаратури від збурювальної дії зовнішніх електростатичних полів. Весь заряд у провіднику збирається на поверхні у шарі атомарної товщини.

Електричне поле – це одна зі складових електромагнітного поля, що існує навколо тіл або частинок, які мають електричний заряд, а також у вільному вигляді при зміні магнітного поля (наприклад, в електромагнітних хвилях). Електричне поле може спостерігатися завдяки силовому впливу на заряджені тіла.

Кількісними характеристиками електричного поля є вектор напруженості електричного поля  й вектор електричної індукції .

Електричне поле викликає переміщення вільних зарядів і може виконувати роботу, а це значить, що воно має енергію.

Енергія електричного поля W задається формулою

. (9.9)

Якщо електричне поле неоднорідне, то його завжди можна розбити на елементарні об’єми dv і вважати, що в межах кожного з них поле є однорідним. Тоді повна енергія електричного поля може бути представлена у вигляді

, (9.10)

де інтегрування проводиться по всьому простору.

Обчислення електричного поля у багатьох випадках можна спростити, застосувавши одну важливу теорему, яка була сформульована М.В.Остроградським ¹¹ у вигляді загально математичної теореми і К.Гауссом – стосовно випадку електричного поля.

Для формулювання згаданої теореми використаємо поняття електричної індукції (електричного зміщення) . Аналогічно до силових ліній введемо поняття ліній електричної індукції, напрям яких співпадає з напрямом вектора електричної індукції, а густина дорівнює величині електричної індукції.

Розглянемо деяку площину S, розташовану в просторі під кутом α до напряму вектора електричної індукції. Величину

(9.11)

називають потоком вектора електричного зміщення (індукції) через дану поверхню. Через D_n позначена проекція вектора на напрям нормалі до площини S. Оскільки густина ліній електричної індукції дорівнює D, то можна також сказати, що потік вектора електричного зміщення через дану поверхню дорівнює повному числу ліній електричного зміщення, що проходять через дану поверхню.

При неоднорідному полі величину повного потоку через поверхню S визначають інтегруванням:

. (9.12)

Відзначимо, що потік є величиною скалярною, причому, можне мати як додатне, так і від’ємне значення, залежно від величини кута.

Розглянемо тепер точковий позитивний заряд q і обчислимо потім електричного зміщення через сферичну поверхню навколо нього. У цьому випадку густина ліній електричної індукції у всіх точках сфери однакова, крім того, всюди . Враховуючи зв’язок між електричною індукцією та напруженістю електричного поля, нескладно показати, що справедливою буде рівність

. (9.13)

Легко побачити, що результат буде аналогічним не лише для будь-якої сферичної поверхні, а й для замкнутої поверхні довільної форми, розташованої навколо заряду. Тобто, враховуючи вирази (9.12) та (9.13), можна записати:

. (9.14)

Формула (9.14) виражає зміст теореми Остроградського-Гаусса, згідно з твердженням якої потік електричного зміщення через замкнуту поверхню дорівнює алгебраїчній сумі всіх зарядів, розташованих всередині поверхні.

Співвідношення, яке виражає теорему Остроградського-Гаусса у диференціальній формі, називають рівнянням Пуассона:

, (9.15)

де – об’ємна густина заряду.

В же йшла мова про те, що тверді тіла мають різні властивості стосовно взаємодії з електричним полем. Наприклад, внісши в електричне поле провідник (метал), ми спостерігатимемо наявність його впливу на величину поля. При дії на провідники зовнішнього електричного поля частина металу, що розміщена ближче до позитивного заряду, який створює електричне поле, набуває негативного заряду, протилежна частина заряджена позитивно. Такий ефект пояснюється електростатичною індукцією.

Що відбуватиметься, якщо в поле внести діелектрик, в якому практично відсутні вільні заряди? Як показують досліди, при піднесенні діелектрика до зарядженого електрометра стрілка також відхилиться, як і у випадку провідника. Але ж у діелектрику заряди переміщуватися не можуть. Яким чином тоді на діелектрику виникають електричні заряди?

Якщо внесений в електричне поле провідник розділити на окремі частини, то кожна з них після зняття зовнішнього поля виявиться зарядженою. А от частини діелектрика при такому досліді будуть нейтральними. Тобто, просторового розділення зарядів не відбулося.

Виявляється, що виникнення зарядів на діелектрику спричиняє ефект, який у фізиці називають поляризацією діелектриків, а заряди, що виникають при цьому, відповідно називають поляризаційними.

У діелектриках носії зарядів обох знаків у звичайних умовах зв’язані між собою, і можуть зміщуватися лише на незначні віддалі, в межах однієї молекули. При відсутності зовнішнього електричного поля рівномірність і хаотичність розподілу молекул в тілі визначає електричну нейтральність діелектрика в цілому. При накладанні зовнішнього поля кожна молекула дещо деформується, внаслідок чого вона стає диполем – утворенням, яке характеризується наявністю на кінцях заряду певного знаку.

Кожен диполь має певний електричний момент, величину якого можна розрахувати за формулою

,

де вектор зміщення вважають напрямленим від негативного заряду до позитивного.

Для кількісної характеристики ефекту поляризації діелектрика використовують спеціальну фізичну величину, яку називають вектором поляризації, і яка дорівнює електричному моменту одиниці об’єму діелектрика:

. (9.16)

Для однорідних діелектриків значення вектора поляризації однакове по всьому об’єму тіла, і поляризацію в цьому випадку називають однорідною.

Діелектрична сприйнятливість – фізична величина, що характеризує властивість речовини поляризуватись, тобто змінювати свою поляризацію під дією електричного поля

. (9.17)

Для анізотропного середовища κ_ij – тензор. Діелектрична сприйнятливість пов’язана з діелектричною проникністю:

. (9.18)

Тому діелектрична проникність має ті самі властивості (залежність від різних параметрів середовища і зовнішніх умов), що й діелектрична проникність. В системі СІ діелектрична сприйнятливість – безрозмірна величина. У діелектриків вона як правило додатна, для вакууму κ = 0.

Р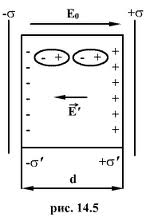 озглянемо однорідне діелектричне середовище певної сталої ширини (наприклад, плаский конденсатор). При накладанні зовнішнього електростатичного поля напруженість всередині діелектрика складатиметься з двох компонентів: поля , створеного зовнішнім полем, і поля , викликаного поляризованим діелектриком (див. рисунок).

Величина першого компонента дорівнює σ/ε₀, де σ – поверхнева густина заряду на обкладинках конденсатора. Дія поляризованого діелектрика проявиться через поляризаційні заряди, тому , де σ' – поверхнева густина поляризаційних зарядів. Отже,

. (9.19)

Різницю між зарядом обкладинок і поляризаційним зарядом часто називають вільним зарядом.

Раніше ми вводили поняття електричного зміщення у вакуумі. У загальному випадку, для довільного діелектрика вектор електричного зміщення буде визначатися за формулою

. (9.20)

Для випадку однорідного діелектрика, як випливає з формули (9.19)

, (9.21)

тобто, у випадку однорідного діелектрика електричне зміщення всередині співпадає з електричним зміщенням у вакуумі, створеним лише зарядами обкладинок конденсатора.

Р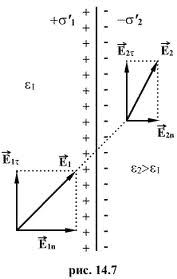 озглянемо тепер межу двох однорідних і однорідно поляризованих діелектриків 1 і 2. У кожному з діелектриків поблизу поверхні розділення з’являться поляризаційні заряди з густинами та , що матимуть різні знаки. Границя розділення діелектриків виявиться зарядженою з поверхневою густиною заряду , внаслідок чого з’явиться додаткове електричне поле , перпендикулярне до межі розділення і напрямлене в кожному з діелектриків у протилежні боки.

Врахувавши довільність напряму зовнішнього електричного поля, позначимо напруженості полі в кожному з діелектриків через і , і розкладемо кожний з векторів на дві складові – паралельну та перпендикулярну до границі розділення. Оскільки електричне поле зарядів поверхні розділення перпендикулярне до цієї поверхні, то паралельні складові поля не зміняться, і їхні значення будуть однаковими:

. (9.22)

Нормальні ж складові будуть різними, і їх різниця дорівнюватиме

,

де P_1n і P_2n – нормальні складові вектора поляризації у кожному з діелектриків. Отже, кількості силових ліній, що проходить через одиницю поверхні розділення в діелектриках 1 і 2 не рівні між собою, а це означає, що частина їх переривається на межі розділення. А це, в свою чергу, означає зміну напряму силових ліній при проходження через границю розділення двох діелектриків.

Деякі хімічні сполуки у твердому стані мають достатньо незвичні властивості. Вперше знайдені в кристалах сегнетової солі, ці властивості дали назву подібним діелектрикам, які почали називати сегнетоелектриками (чи ферроелектриками). Детально діелектрична властивості сегнетової солі були проведені І.В.Курчатовим і П.П.Кобеко¹².

Сегнетова сіль є подвійною натрій-калієвою сіллю винної кислоти , кристали якої належать до ромбічної системи. ці кристали проявляють різку анізотропію властивостей.

Першою особливістю є надзвичайно висока діелектрична проникність (біля 10 000) в певному температурному діапазоні. Друга особливість – це специфіка залежності електричної індукції від напруженості електричного поля, де відсутня пропорційність. Власне, така залежність є різною для різних сегнетоелектриків.

Третьою особливістю є той факт, що значення електричного зміщення в сегнетовій солі визначається не лише напруженістю зовнішнього електричного поля, але й попередніми станами поляризації. Це явище називають діелектричним гістерезисом.

П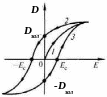 ри початковому збільшенні поля наростання зміщення описується гілкою 1 кривої, яка не є лінійною. Якщо потім зменшувати електричне поле, то зменшення зміщення відбуватиметься по гілці 2. коли величина поля досягає нульового значення, зміщення не дорівнює нулю і зображується відрізком D_зал.

Тобто, у сегнетовій солі існує залишкова поляризація, що робить кристал поляризованим навіть при відсутності зовнішнього електричного поля. Для ліквідації цієї залишкової поляризації потрібно створити електричне поле протилежного знаку -Е_с. при подальшій циклічній зміні електричного поля зміщення описується гілкою 3, що у результаті приводить до утворення петлеподібної кривої – петлі гістерезису.

Такі властивості характерні для всіх сегнетоелектриків, а відмінність спостерігається лише у ширині гістерезисної петлі.

Сегнетоелектричні властивості є дуже залежними від температури середовища. При температурах, що перевищують деяке значення Т_к (різне для різних сегнетоелектриків), сегнетоелектрик перетворюється у звичайний діелектрик. Таку температуру називають температурою (чи точкою) Кюрі ¹³.

При температурі Кюрі, пов’язаній з фаховим переходом другого роду, у всіх випадках фазових переходів зникаю будь-який тип атомної впорядкованості, наприклад, впорядкованість електронних спінів (для сегнетоелектриків), атомних магнітних моментів (для феромагнетиків), впорядкованість розташування атомів різних компонентів сплаву у вузлах кристалічної гратки (для сплавів) тощо. Поблизу точки Кюрі спостерігають різкі аномалії фізичних властивостей (п’єзоелектричних, електрооптичних, теплових). Для деяких сегнетоелектриків, зокрема, для сегнетової солі, спостерігають дві точки Кюрі (+22,5С та –15С), у проміжку між якими і проявляються сегнетоелектричні властивості.

Одним з важливих застосувань сегнетоелектриків є створення на їх основі конденсаторів, для яких характерним буде висока ємність при малих розмірах і високій якості роботи.

Крім сегнетоелектриків, окрему важливу групу діелектриків складають п’єзоелектрики. У 1880 році відомий вже П’єр Кюрі разом зі своїм братом Жаком Кюрі ¹⁴ виявили п’єзоелектричний ефект – явище поляризованості під дією тиску на кристали цукру, кварцу, турмаліну, топазу і тієї ж сегнетової солі. У 1881 році вони відкрили протилежний ефект – деформацію кристалів під дією електричного поля. Це дозволило використовувати кварц як перетворювач електричних коливань в звукові. Технічні розробки п’єзоелектричних явищ привели до створення малогабаритних випромінювачів і приймачів ультразвуку.

Тема №10. «Електростатика. Постійний електричний струм»

1. Провідники в електричному полі.

2. Енергія електростатичного поля.

3. Різниця потенціалів. Напруга.

4. Електроємність. Конденсатори. З’єднання конденсаторів.

5. Постійний електричний струм. Закон Ома.

6. Потужність. Закон Джоуля-Ленца. Електрорушійна сила.

7. З’єднання опорів. Резистори.

8. Правила Кірхгофа. Шунт. Додатковий опір.

9. Нагрівні прилади. ТЕНи.

10. Електричний струм у газах. Плазма.

11. Природа носіїв струму в металах.

Якщо електричні заряди в якомусь провіднику заходяться у рівновазі, тобто в ньому відсутнє перенесення заряду, то напруженість поля в будь-якій точці всередині провідника дорівнює нулю. Дійсно, якби ця умова не виконувалася, то рухомі електричні частинки під дією сил поля почали б рухатися, що порушило б рівновагу. З рівняння Пуассона (9.15) випливає, що об’ємна густина заряду всередині провідника також дорівнює нулю. Тобто, при відсутності електричного струму заряди розподіляються лише на поверхні провідника.

З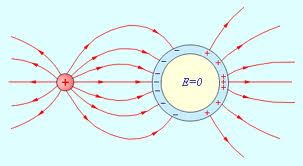 аряди у стані рівноваги розподіляються по поверхні провідника завжди, незалежно від того, яким чином вони виникли. Якщо замкнутий порожнистий металевий провідник знаходиться у зовнішньому електричному полі, то на ньому з’являться індукційні заряди. Вони будуть зосереджені лише на зовнішній поверхні, а електричне поле і у товщині металу, і всередині контуру дорівнюватиме нулю. Тому порожнистий металевий провідник екранує електричне поле усіх зовнішніх зарядів. Це явище широко використовують для захисту чутливих електричних приладів від збурень зовнішній полів.

Однак, замкнутий порожнистий провідник екранує лише поле зовнішніх зарядів. Якщо заряд знаходиться всередині порожнини, то індукційні заряди виникнуть не лише на зовнішній частині провідника, але й на внутрішній. Розподіл цих зарядів буде таким, щоб повне поле, створене індукованими зарядами та зарядом, розташованим всередині порожнини, в будь-якій точці провідника було рівним нулю. Але всередині порожнини поле не буде н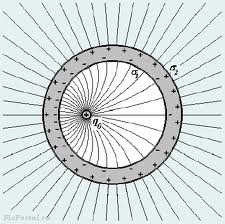 ульовим, і тут будуть проходити силові лінії, які з’єднуватимуть центральний заряд індукційними зарядами на внутрішній поверхні провідника. Індукційні заряди на зовнішній поверхні викличуть появу поля у зовнішньому середовищі. Отже, замкнута провідна поверхня не екранує поле електричних зарядів, розташованих всередині неї.

Для розуміння властивостей електричного поля велике значення має поняття різниці потенціалів, або електричної напруги.

Нехай електричний заряд переміщується у деякому електричному полі з точки 1 у точку 2. Оскільки на заряд в електричному полі діє сила, то при такому переміщенні буде виконана певна робота А₁₂. Очевидно, що при зворотному переміщенні буде виконана така ж за величиною, але протилежна за знаком робота: А₂₁ = – А₁₂.

Н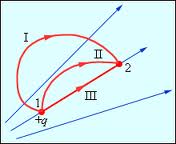 ескладно довести, що в електростатичному полі робота з переміщення заряду не залежить від форми шляху, яким рухається заряд, і визначається лише розташуванням точок 1 і 2 – початку й кінця шляху. Справді, якби це було не так, то при переміщенні заряду замкнутим контуром була б виконана деяка, відмінна від нуля робота, що суперечить закону збереження енергії, оскільки заряд повернувся у вихідну точку електростатичного поля, що означає відсутність змін у цьому полі.

Уявимо, що відбувається переміщення одиничного заряду (+1). Тоді робота, виконана при такому переміщенні, залежатиме від властивостей наявного електричного поля і може слугувати його характеристикою. Її називають різницею потенціалів точок 1 і 2 або електричною напругою між точками 1 і 2.

Отже, різниця потенціалів двох точок електростатичного поля вимірюється роботою, яку здійснюють сили поля при переміщенні одиничного заряду з однієї точки в іншу.

Знаючи напруженість поля в кожній точці, можна обчислити й різницю потенціалів будь-яких двох точок:

, (10.1)

де ds – елемент переміщення заряду, E_s – проекція вектора напруженості поля на напрямок .

Якщо переміщується не одиничний заряд, а довільний величиною q, то робота, що при цьому виконується, дорівнюватиме

. (10.2)

Часто ведуть мову про потенціал чи напругу в даній точці. Однак, слід взяти до уваги, що при цьому все одно мають на увазі різницю потенціалів, вибираючи іншу точку «на нескінченості», тобто на значній віддалі від заряджених тіл.

Розглянемо два провідники, кожен з яких характеризується наявністю певного заряду. Зі сказаного раніше випливає, що вони створюватимуть навколо себе певне поле, і при невеликих віддалях між провідниками можна уявити, що всі лінії зміщення, які виходять з одного провідника, закінчуються на іншому. Таку пару провідників називають простим конденсатором (або просто конденсатором), а самі провідники – обкладинками.

Оскільки лінії зміщення в конденсаторі починаються й закінчуються на обкладинках, то звідси випливає, що заряди на них однакові за величиною, але протилежні за знаком.

Напруженість поля в довільній точці між обкладинками конденсатора завжди пропорційна величині заряду обкладинок:

. (10.3)

Коефіцієнт С в цій формулі називають електричною ємністю конденсатора або просто його ємністю.

Ємність конденсатора визначається зарядом на кожній з обкладинок, якщо напруга між ними дорівнює одиниці. Одиницею вимірювання ємності є фарада (Ф = Кл/В). На практиці застосовують дрібніші одиниці вимірювання – мікрофарада (1 мкФ = 10^-6 Ф), пікофарада (1 пФ = 10^-12 Ф).

Р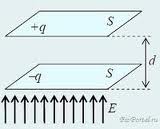 озглянемо деякі приклади. Якщо на одиниці площі обкладинок є заряд σ і діелектриком між ними є вакуум, то повна напруга між обкладинками дорівнюватиме

, (10.4)

Для повної площі пластин вираз для ємності конденсатора матиме вигляд:

. (10.5)

Якщо ж простір між обкладинками заповнений деяким діелектриком з діелектричною проникністю ε, то ємність буде в ε разів більшою:

. (10.6)

Н ехай конденсатор складається з двох коаксіальних циліндрів з радіусами а (внутрішній) і b (зовнішній). Довжину циліндрів вважатимемо суттєво більшою порівняно із зазором між ними. Напруга між циліндрами дорівнюватиме

, (10.7)

де q₁ – заряд на одиницю довжини циліндрів. Тому ємність циліндричного конденсатора у вакуумі на кожну одиницю довжини складатиме величину

. (10.8)

Якщо віддаль між обкладинками циліндричного конденсатора значно менша від різниці їх радіусів, то вираз (10.8) можна спростити, розклавши логарифм у ряд і використавши лише перший доданок цього ряду:

. (10.9)

Отже, у цьому випадку ємність можна обчислити, використовуючи формулу для плаского конденсатора.

Я кщо напруга на конденсаторі перевищує певне значення, то конденсатор «пробивається», тобто між його обкладинками виникає електрична іскра (або всередині діелектрика, або на його поверхні), і конденсатор виходить з ладу. Тому кожен конденсатор характеризують не лише його ємністю, але й робочим значенням напруги.

Для того, щоб отримати для даної напруги потрібне значення ємності, конденсатори об’єднують в батареї.

При паралельному з’єднанні конденсаторів заряд на батареї складається з суми зарядів на кожному конденсаторі, тому ємність такої батареї обчислюють за формулою

. (10.10)

Допустима напруга для всіх паралельно з’єднаних конденсаторів у батареї буде однаковою.

При послідовному з’єднанні загальна напруга батареї дорівнюватиме сумі напруг на кожному конденсаторі

,

тому для ємності такої батареї справедливим буде вираз

. (10.11)

Для послідовно з’єднаних конденсаторів робоча напруга кожного конденсатора буде меншою, ніж для батареї в цілому.

При необхідності перенесення електричного заряду в просторі потрібно створити такі умови, які б цьому сприяли. Основною вимогою тут є мінімізація втрат заряджених носіїв. Розглянемо, що відбувається з цієї точки зору в різних речовинах, матеріалах, середовищах. При цьому всяке переміщення електричних зарядів називатимемо електричним струмом. За напрям струму прийнято вважати напрям переміщення позитивно заряджених носіїв.

Для початку візьмемо метали. Їх будова сприяє добрій провідності, оскільки в металах є значна кількість вільних електронів, які під дією зовнішнього електричного поля можуть достатньо легко рухатися вздовж провідника. Позитивно заряджені іони, закріплені у вузлах кристалічної гратки, участі в перенесенні заряду не беруть. Отже, струм у металах протікає в напрямі, протилежному до напряму руху вільних електронів (їх ще називають електронами провідності).

Для кількісної характеристики електричного струму служать дві основні величини: густина заряду та сила струму.

Густина струму дорівнює величині заряду, що проходить за одиницю часу через одиничну поверхню, перпендикулярну до ліній струму (ліній, вздовж яких рухаються заряджені частинки):

, (10.12)

і є, власне, векторною величиною, оскільки швидкість – це вектор.

Сила струму і в будь-якому провіднику дорівнює величині заряду, що проходить за одиницю часу через повний переріз провідника:

. (10.13)

Оскільки і величина заряду, і час є скалярами, то й сила струму є також величиною скалярною.

Знаючи вектор густини струму в будь-якій точці поперечного перерізу провідника, можна виразити силу струму через його поздовжні N складових:

. (10.14)

Одиницею вимірювання сили струму є Ампер (А). На практиці часто використовують менші за розміром одиниці – міліампер (1 мА = 10^-3 А) або мікроампер (1 мкА = 10^-6 А). Одиницею вимірювання густини струму є А/м².

Якщо густина і сила струму в провіднику з часом не змінюються, то кажуть, що має місце постійний струм. Для постійного струму сила струму однакова для усіх перерізів провідника.

Якщо у провіднику є струм, то потенціал в різних його точках вже не є однаковим. При наявності струму в провіднику створюється спад напруги вздовж нього, тобто існує складова напруженості поля E_t, напрямлена вздовж провідника. А це, в свою чергу, означає, що силові лінії вже не є перпендикулярними до поверхні провідника. Вони нахилені в напрямку струму на деякий кут α.

Спад напруги означає також наявність у провіднику явища, яке приводить до зменшення швидкості переміщення зарядів – електричного опору. При незмінному стані провідника (постійній температурі тощо) для кожного провідника спостерігається однозначна залежність між прикладеною напругою U та силою струму і в ньому. Цю залежність називають вольт-амперною характеристикою даного провідника.

Для багатьох провідників, особливо для металів. Ця залежність виглядає достатньо просто – сила струму в провіднику прямо пропорційна прикладеній напрузі. Коефіцієнт пропорційності називають електропровідністю провідника, а величину, обернену до електропровідності – електричним опором. Електропровідність і опір залежать від роду речовини провідника, його геометричних розмірів і форми, а також від стану провідника. Формулу такої залежності називають законом Ома:

. (10.15)

Електричний опір вимірюють в Омах. Тобто, 1 Ом – це опір провідника, в якому при прикладеній напрузі 1 В виникає струм силою 1 А. Для провідників циліндричної форми можна записати такий вираз залежності опору від параметрів провідника:

, (10.16)

де l – довжина провідника, S – його поперечний переріз. Коефіцієнт пропорційності ρ залежить від роду речовини і називається питомим опором провідника. Це опір куба з ребром 1 м з даної речовини при протіканні струму паралельно одному з ребер. Одиниця вимірювання питомого опору – Ом^.м.

Речовина	Питомий опір в Ом.м при кімнатній температурі
Срібло	1,6.10-8
Мідь	1,8.10-8
Ніхром (67,5% Ni, 15% Cr, 16% Fe, 1,5% Mn)	1,1.10-6
Графіт	3.10-5
NaCl, 10%-ний водний розчин	8,25.10-2
Хімічно чиста вода	~106
Порцеляна	~1013
Бурштин, плавлений кварц	>1018

Питомий опір залежить не лише від роду речовини, але й від її стану, в першу чергу, від температури. Ця залежність не є лінійною. Однак, для багатьох провідників, зокрема, для металів, така залежність є не надто великою, і може бути виражена формулою

, (10.17)

де ρ₀ – значення питомого опору при абсолютному нулі температури, а коефіцієнт α називають температурним коефіцієнтом опору

, (10.18)

який дає відносний приріст опору при збільшенні температури провідника на один градус. Даний коефіцієнт може мати як додатне, так і від’ємне значення. Наприклад, для всіх металів спостерігається підвищення опору з ростом температури (α > 0), а для електролітів α < 0, тобто їх опір при підвищенні температури падає.

Закон Ома у вигляді виразу (10.15) використовують для випадку, коли трубки струму мають постійний переріз. Однак, така ситуація трапляється не завжди. При складнішій формі провідника, для циліндричного чи сферичного конденсаторів наведений вигляд закону Ома вже не придатний. Тому він має інший варіант, який може бути застосований для довільного провідного середовища. Це так званий закон Ома в диференціальній формі:

, (10.19)

де – вектор напруженості електричного поля всередині провідника, – вектор густини струму. Коефіцієнт λ має зміст питомої електропровідності середовища .

Існування вольт-амперної залежності дозволяє вимірювати опір провідників за допомогою амперметра і вольтметра. При цьому важливо, щоб струм, що відгалужується на вольтметр, був суттєво меншим порівняно зі струмом у провіднику.

Якщо створити в колі струм за допомогою конденсатора із замкнутими обкладинками, то перетікання зарядів з однієї обкладинки на іншу буде супроводжуватися зменшенням, згідно із законом Ома, сили струму. Ця обставина є спільною для всіх електростатичних полів: таке поле завжди переміщує заряди таким чином, що б різниця потенціалів зменшувалася.

Для отримання постійного струму потрібна дія сторонніх сил. Всі пристрої, в яких ці сили виникають, називають джерелами струму. Прикладом джерела струму може бути гальванічний елемент.

Розглянемо довільну ділянку електричного кола, через яку протікає електричний струм. Якщо сила струму дорівнює і, то за час t через ділянку пройде заряд it, й, відповідно буде виконана робота

. (10.20)

Величину роботи, виконаної за одиницю часу, можна обчислити за формулою

. (10.21)

Цю величину називають потужністю електричного струму. Одиницею вимірювання потужності є Ватт (1Вт = 1В ^. 1А). Якщо у провіднику справедливий закон Ома, то потужність можна обчислити за альтернативними формулами:

. (10.22)

Перша частина формули (10.22) для оцінювання виконаної струмом роботи була встановлена незалежно двома вченими – Е.Х.Ленцом та Дж.Джоулем ¹⁵ і сформульована у вигляді такого твердження (закон Джоуля-Ленца): кількість теплоти, що виділяється струмом у провіднику, пропорційна квадрату сили струму і опору провідника.

Будь-яке джерело струму, включене в електричне коло, стає ділянкою цього кола, через яку також протікає струм. А, отже, воно характеризується наявністю певного опору r, який називають внутрішнім опором. Враховуючи хімічну (як правило) природу джерела струму, наприклад, гальванічного елемента, закон збереження енергії для такого кола матиме вигляд

, (20.23)

де Q_Х – енергія, що вивільняється при хімічних реакціях, А – робота струму, Q_Т – кількість тепла, що виділяється (чи поглинається) джерелом для підтримування постійної температури. Отже, в роботу струму перетворюється не вся енергія хімічних реакцій, а лише різниця

.

Максимальна робота при даній постійній температурі є певною долею енергії Q_Х , і, як і ця енергія, пропорційна величині заряду, що пройшов по колу. Тому можна записати:

, (20.24)

де  – максимальна робота даної хімічної реакції (чи реакцій), розрахована на одиницю заряду. Вона отримала назву електрорушійної сили (е.р.с.).

Для повної роботи струму в електричному колі отримає рівність

, (10.25)

а, поділивши обидві частини на величину заряду , отримаємо:

. (10.26)

Отриманий закон (10.26) називають законом Ома для повного (замкнутого) кола. Суму опорів у знаменнику називатимемо повним опором кола. Розмірність е.р.с. така сама, як і у напруги – Вольт.

В раховуючи вигляд закону Ома, нескладно зробити висновок, що з’єднавши кілька опорів послідовно, ми отримаємо один опір величиною

, (10.27)

при цьому на кожному з резисторів буде свій спад напруги, який визначатиметься тим же законом Ома. Через всі опори такого з’єднання протікатиме однаковий струм.

Паралельне з’єднання реалізує ситуацію, коли спад напруги буде однаковим для всіх резисторів, а сила струму через кожен з них визначатиметься величиною його опору. Загальний опір такої ділянки можна розрахувати з формули

. (10.28)

Дотепер ми розглядали найпростіші електричні кола, які складалися лише з одного замкнутого контуру. Але на практиці необхідно з’єднувати провідники в набагато складніші контури, з місцями розгалужень двох і більше ділянок. Кожна з ділянок такого складного контуру може містити джерело з е.р.с. і характеризується певним опором. Виникає питання про розрахунок сили струму, що протікатиме кожною з ділянок.

Р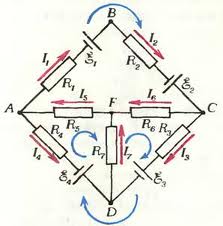 озглянемо один з можливих варіантів такого розгалуженого електричного кола в точці, наприклад, F. У цій точці сходяться три ділянки (5, 6 і 7), через які протікають струми відповідно І₅, І₆ та І₇. домовимося вважати струм додатнім, якщо він напрямлений до точки розгалуження (струми І₆ та І₇), і від’ємним, коли струм напрямлений від неї (І₅).

Алгебраїчна сума струмів (І₆ + І₇ – І₅) у точці F є зарядом, що надходить в дану точку за одиницю часу. Якщо в колі в цілому струми постійні, то сума струмів в точці F повинна бути рівною нулю, оскільки інакше це означало б зміну потенціалу в точці з часом, що приводило до зміни струмів у колі. Це твердження справедливе для будь-якої точки кола, тобто для довільної точки розгалуження

. (10.29)

Формула (10.29) є аналітичним вираженням першого правила Кірхгофа ¹⁶: алгебраїчна сума сил струмів в ділянках кола, що сходяться в будь-якій точці розгалуження, дорівнює нулю.

Якщо для ділянок довільного замкнутого контуру наведеного кола застосувати закон Ома для ділянки з е.р.с.

,

то отримаємо систему рівностей

,

,

,

.

Додавши почленно записані рівняння, отримаємо зліва нуль, звідки

.

Подібний вираз можна отримати для будь-якого замкнутого контуру, тому в загальному можна записати:

. (10.30)

Рівняння (10.30) виражає друге правило Кірхгофа: для довільного замкнутого контуру сума всіх спадів напруг дорівнює сумі всіх електрорушійних сил у даному контурі.

Тема №11. «Магнетизм. Електромагнетизм»

1. Магнітний потік. Робота з переміщення провідника і контуру зі струмом у магнітному полі.

2. Електромагнітна індукція. Правила Ленца.

3. Явище самоіндукції. Взаємна індукція.

4. Енергія магнітного поля.

5. Магнітне поле в речовині.

6. Типи магнетиків. Діа-, пара- та феромагнетики. Точка Кюрі.

7. Основи теорії Максвелла для електромагнітного поля.

8. Рівняння Максвелла в диференціальній формі.

9. Рух зарядженої частинки в електромагнітному полі.

10. Вимірювання ємнісного, індуктивного та комплексного опору

у колі змінного струму.

11. Електромагнітні методи дослідження матеріалів.

Гідро

Тема №12. «Геометрична оптика»

1. Розвиток уявлень про природу світла.

2. Геометрична оптика.

3. Закон незалежності світлових променів.

4. Основні закони геометричної оптики.

5. Явище повного внутрішнього відбивання, його використання в оптичних лініях зв’язку.

6. Побудова зображень у деяких оптичних системах: плоске дзеркало, сферичне дзеркало, лінза.

Гідро

Тема №13. «Хвильова оптика»

1. Інтерференція світла.

2. Когерентність світлових хвиль. Деякі способи одержання

когерентних хвиль.

3. Дифракція світла.

4. Принцип Гюйгенса-Френеля. Дифракція Френеля.

5. Дифракція Фраунгофера.

6. Дифракційна решітка. Формула Вульфа-Брегга.

7. Застосування дифракції. Визначення довжини хвилі світла за допомогою дифракційної решітки.

8. Визначення показника заломлення рідини рефрактометром.

9. Дисперсія світла. Нормальна та аномальна дисперсія.

10. Поляризація світла. Поляризатори. Природне та поляризоване світло.

11. Подвійне заломлення променів.

12. Штучна оптична анізотропія.

13. Явище повороту площини поляризації.

14. Оптичні методи дослідження товарів, сировини і матеріалів.

Гідро

Тема №14. «Теплове випромінювання»

1. Теплове випромінювання.

2. Фізична природа теплового випромінювання.

3. Закон Кірхгофа. Формула Планка.

4. Закони Стефана-Больцмана та Віна.

5. Пірометри. Визначення сталої Стефана-Больцмана

за допомогою оптичного пірометра.

6. Теплове обладнання при обробці сировини і матеріалів.

Гідро

Тема №15. «Квантова оптика. Дуальна природа світла»

1. Корпускулярно-хвильова природа світла.

2. Фотоефект. Основні закономірності.

3. Формула Ейнштейна.

4. Червона границя фотоефекту.

5. Робота виходу. Затримуючий потенціал.

6. Види фотоефекту: зовнішній, внутрішній, багатофотонний.

7. Застосування фотоефекту.

8. Визначення сталої Планка методом затримуючого потенціалу.

9. Ефект Комптона.

10. Тиск світла.

11. Люмінесценція.

Гідро

Тема №16. «Мікроструктура світу»

1. Лазери (оптичні, квантові генератори, ОКГ). Принципи будови.

2. Спонтанне та вимушене випромінювання.

3. Нерівноважні системи. Активна речовина.

4. Позитивний зворотній зв’язок.

5. Застосування лазерів у науці, техніці, медицині, побуті.

6. Напівпровідникові прилади (діод, тріод).

7. Визначення параметрів напівпровідникових приладів.

8. Застосування напівпровідникових приладів.

9. Мікросхеми. Чіпи. Комп’ютери.

10. Квантовий транзистор. Спіновий транзистор.

11. Квантовий комп’ютер. Спіновий комп’ютер.

Гідро

Тема №17. «Елементи ядерної фізики»

1. Склад атомного ядра. Нейтрони. Протони. Нуклони.

2. Масове число. Ізотопи.

3. Дефект маси. Енергія зв’язку ядра. Розміри і форми ядер.

4. Ядерні сили. Ядерні реакції. Радіоактивність.

5. Взаємодія заряджених частинок, квантів і нейтронів з речовиною.

6. Лічильники частинок і квантів.

7. Візуальні методи спостереження треків.

8. Елементи дозиметрії.

Гідро

1 Очевидно, що рівномірний рух можливий лише по прямій в одному напрямку, інакше переміщення будуть різними.

2 Джеймс Ватт запропонував своєму приятелю, який був власником шахти, замінити коня який працював на підйомнику паровою машиною. Той погодився, але поставив умову, щоб парова машина не поступалася коневі силою. Для цього було вирішено поставити експеримент і замірити, яку саме роботу робить кінь за день. Господар наказав нещадно ганяти бідолашну стару конячину, аби отримати якомога більший результат, тож тварина надірвалася і потім здохла. Насправді, потужність в 1 к.с. є надмірним навантаженням для більшості коней, і зазвичай під час роботи вони її не розвивають.

3 Дисипація (лат. dissipatio – розсіювання) – процес розсіювання чого-небудь, наприклад, енергії.

4 За формальним означенням моль – це кількість речовини, виражена в грамах, що чисельно дорівнює її молекулярній масі й відзначається тим, що одному молю будь-якої речовини відповідає однакова кількість молекул. А саме, 1 моль містить стільки молекул (атомів, іонів, інших структурних елементів речовини), скільки атомів у 0,012 кг вуглецю ¹²С, тобто дорівнює сталій Авогадро. Позначення «моль» введене у 1893 році Вільгельмом Оствальдом і походить від слова «молекула».

5 Кількістю теплоти називають енергію, яку тіло отримує або втрачає в результаті теплопередачі,. Кількість теплоти позначається літерою Q та в системі СІ вимірюється у Джоулях.

6 Закон Джоуля-Коппа базується на законі Дюлонга-Пті й описує теплоємність складних кристалічних тіл, тобто таких, що складаються з кількох хімічних елементів. Кожен атом у молекулі має три ступені вільності і енергію Е_а = 3kT.

7 Поверхнева енергія – це енергія, потрібна на виконання роботи зі збільшення площі поверхні на одиницю. Вимірюється в Дж/м² або в ерг/см².

8 Згідно з цією гіпотезою, реальні дискретні об’єкти замінюються спрощеними моделями, які подаються як матеріальний континуум, тобто матеріальне середовище, маса якого нерозривно розподілена по об’єму. Така ідеалізація спрощує реальну дискретну систему і дозволяє використовувати для її опису добре розвинений математичний апарат числення нескінченно малих величин та теорію нерозривних функцій.

9 Шарль Огюстен де Кулон (1736-1806) – французький військовий інженер і вчений-фізик, дослідник електромагнітних і механічних явищ; член Паризької Академії наук. На його честь названі одиниця вимірювання електричного заряду і закон взаємодії електричних зарядів.

10 Діелектрична проникність (діелектрична стала) середовища ε – це безрозмірна величина, що характеризує ізоляційні властивості середовища. Вона показує, у скільки разів взаємодія між зарядами в однорідному середовищі менша, ніж у вакуумі.

11 Карл Фрідріх Гаусс (1777-1855) – німецький математик, фізик, астроном і геодезист. Його вважають одним з найвидатніших математиків світу. Винайшов і створив (спільно з Вебером) перший електричний телеграф.

Михайло Васильович Остроградський (1801-1861) – видатний український математик. Праці М.В.Остроградського присвячено аналітичній механіці, гідромеханіці, теорії пружності, небесній механіці, математичній фізиці, матаналізу і теорії дифрівнянь. Розвинув теорію хвиль на поверхні важкої ідеальної рідини. Досліджував малі коливання пружних тіл. Приятелював з Т.Г.Шевченком.

12 Ігор Васильович Курчатов (1903-1960) – видатний радянський фізик, організатор і керівник робіт в галузі атомної науки і техніки в СРСР, академік АН СРСР.

Павло Павлович Кобеко (1897-1954) – радянський фізик, досліджував механічні і фізичні властивості діелектриків. Йому належать важливі роботи по сегнетоелектриці. Вперше почав досліджувати фізичні властивості аморфних тіл і полімерів.

13 Названа на честь французького вченого-фізика П’єра Кюрі (1859-1906), одного з перших дослідників радіоактивності, члена Французької АН, лауреата Нобелівської премії з фізики за 1903 рік.

14 Поль-Жак Кюрі (1856-1941) – французький фізик-дослідник. Основний напрямок досліджень – мінералогія.

15 Еміль Християнович (Генріх Фрідріх Еміль) Ленц (1804-1965) – відомий російський вчений-фізик. В основному працював в галузі електромагнетизму. Сформулював закон індукції (правило Ленца), провів досліди з доведення явища Пельтьє та ін.

Джеймс Пресскотт Джоуль (1818-1889) – англійський фізик і пивовар. Вивчав природу тепла й встановив її зв’язок з механічною роботою. Це привело до ідеї збереження енергії, і, в свою чергу, до розробки першого закону термодинаміки. На честь Джоуля названа одиниця вимірювання енергії.

16 Густав Роберт Кірхгоф (1824-1887) – один з видатних фізиків ХІХ століття. Разом з німецьким вченим Бунзеном заклав основи спектрального аналізу, відкрив цезій та рубідій. Встановив один з законів випромінювання (закон Кірхгофа) та правила для розрахунку електричних кіл (правила Кірхгофа).