Проекти вічних двигунів першого роду.

Особливий розділ даного напрямку досліджень присвячений вивченню теплоємності твердих тіл. Справа в тому, що, на відміну від газів чи рідин, структуру твердого тіла можна умовно поділити на дві групи: атоми кристалічної гратки та вільні електрони. Кожна з цих груп робить свій внесок у теплоємність тіла, причому при різних умовах внесок кожної з груп різний.

Існує декілька теорій теплоємності твердого тіла:

• закон Дюлонга-Пті і закон Джоуля-Коппа⁶. Обидва закони виведені з класичних уявлень і з певною точністю справедливі лише для нормальних температур (приблизно в межах 15-100°C);

• квантова теорія теплоємності Ейнштейна;

• квантова теорія теплоємності Дебая.

Закон Дюлонга-Пті визначає питому теплоємність твердого тіла за формулою

, (6.3)

де c – питома теплоємність, R – універсальна газова стала, μ – молярна маса.

Закон відкрили в 1819 році П’єр Дюлонг і Алексіс Пті. Для того, щоб підвищити температуру, потрібно збільшити кінетичну енергію руху кожного з атомів твердого тіла. Однак, внаслідок сильної взаємодії атомів між собою, збільшення кінетичної енергії потребує рівного за величиною збільшення потенціальної енергії. Тому теплоємність твердого тіла вдвічі більша за теплоємність ідеального газу.

За моделлю Дюлонга-Пті тверде тіло розглядається як сукупність гармонічних осциляторів. В одному молі твердого тіла таких осциляторів 3N_A, тому що з кожним атомом (молекулою) твердого тіла можна зв’язати три незалежні осцилятори, які здійснюють коливання вздовж трьох взаємно перпендикулярних осей.

За теоремою про рівнорозподіл енергії по ступенях вільності на кожний осцилятор припадає енергія kT. Тому внутрішня енергія 1 моля твердого тіла

, (6.4)

звідси молярна теплоємність за сталого об'єму

(6.5)

Отже, молярна теплоємність твердих тіл рівна 3R й не залежить від температури. Однак, такий висновок, як мінімум, не відповідає дослідним фактам. В дослідах виявлено, що за умови T → 0 питома молярна теплоємність зменшується за законом Т³.

Для справедливості закону Дюлонга-Пті необхідно, щоб енергії теплового руху вистачало для збудження всіх можливих типів коливань у твердому тілі. При низьких температурах деякі з коливань не збуджуються. Це явище зумовлене законами квантової статистики. Тому при низьких температурах закон Дюлонга-Пті не діє.

Альбертом Ейнштейном була запропонована модель теплоємності твердого тіла, яка виходила з припущення, що тверде тіло складається з осциляторів з певною власною частотою ω. При розрахунку Ейнштейн вирахував квантову природу осциляторів. В цьому випадку середня енергія одного осцилятора становить

, (6.6)

де – енергія квантового осцилятора за нескінченно низької температури, – енергія кванта, що випромінюється чи поглинається внаслідок переходів між коливальними рівнями гармонічного осцилятора.

Для молярної теплоємності в межах цієї моделі отримуємо:

. (6.7)

За моделлю Ейнштейна , якщо ; , якщо . Але за низьких температур не пропорційна Т³.

Теорія Ейнштейна пояснює закон Дюлонга-Пті при високих температурах і падіння теплоємності до нуля при низьких температурах, однак не може кількісно відтворити закон цього падіння. Недоліком теорії є те, що вона не враховує взаємодію між осциляторами.

Врахувавши таку взаємодію, в 1912 році Петер Дебай побудував теорію теплоємності, яка правильно відтворює кубічну залежність теплоємності від температури при низьких температурах.

Закон Дебая стверджує, що при низьких температурах теплоємність твердого тіла зростає пропорційно кубу температури. Цей закон справедливий для діелектриків і напівпровідників при температурах, набагато менших за температуру Дебая, яка є характеристикою кожної конкретної речовини. Знаючи температуру Дебая, теплоємність при сталому об’ємі можна оцінити за формулою

, (6.5)

де N – число атомів, k – стала Больцмана, Т – температура, – температура Дебая.

Наведемо значення температури Дебая для деяких речовин:

Алюміній	429 К	Срібло	225 К	NaCl	280 К
Кадмій	186 К	Тантал	240 К	Свинець	96 К
Хром	610 К	Біле олово	195 К	α-марганець	476 К
Мідь	344,5 К	Титан	420 К	Нікель	440 К
Золото	165 К	Вольфрам	405 К	Платина	240 К
α-залізо	464 К	Цинк	300 К	Лід	192 К
Кремній	640 К	Алмаз	2200 К	KBr	180 К

Внутрішня енергія за означенням є функцією стану, тому її можна записати у вигляді деякої функції параметрів стану

. (6.6)

Із рівняння стану

. (6.7)

Можемо знайти один з параметрів стану, припустимо тиск р, і підставити у рівняння для внутрішньої енергії. Тоді внутрішню енергію можна записати як

. (6.8)

Залежність такого типу має назву калоричного рівняння. Як і рівняння стану, так і калоричне рівняння не можуть бути отримані у рамках термодинаміки. Їх вигляд знаходять із досліду.

Оскільки внутрішня енергія є функцією стану, можна взяти від неї повний диференціал:

. (6.9)

Підставимо цей диференціал у вираз для першого начала термодинаміки й отримаємо:

_(6.10)

За означенням теплоємності

. (6.11)

Ми отримали загальне рівняння для теплоємності.

Найпростішим було б знайти калоричне рівняння для ідеального газу, оскільки його рівняння стану відоме – це рівняння Клапейрона

.

Для ідеального газу внутрішня енергія залежить лише від температури, і калоричне рівняння набуває вигляду

. (6.12)

Цей експериментальний факт має назву закону Джоуля. Вигляд функції не може бути визначений методами термодинаміки, вона може бути лише виражена через теплоємність. Оскільки внутрішня енергія ідеального газу не залежить від об’єму

; ,

тоді повна внутрішня енергія дорівнює інтегралу

(6.13)

від початкового до кінцевого стану.

Якщо сумістити початковий стан з нулем температури, то

. (6.14)

Але знову ж таки, розв’язати таке рівняння неможливо, оскільки теплоємність є невідомою функцією стану. Хоча для великої кількості газів у досить великих межах зміни теплоємність є сталою величиною:

. (6.15)

Розглянемо друге начало термодинаміки. Саді Карно теоретично розглянув роботу ідеальної теплової машини, що складається з одного моля ідеального газу, який є робочим тілом. Згідно з першим началом термодинаміки кількість теплоти, отримана газом, в результаті всього циклу повинна дорівнювати виконаній за цикл роботі:

. (6.16)

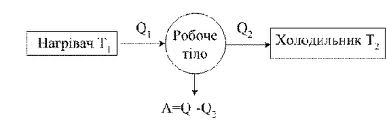
Отже, в результаті циклу газ, отримавши кількість теплоти Q₁ від нагрівача і передавши частину цієї теплоти Q₂ холодильнику, виконує зовнішню роботу, що дорівнює А.

Віддавання теплоти холодильнику є необхідною умовою виконання роботи, отже A < Q₁, тобто розглянута теплова машина не може всю отриману кількість теплоти повністю переводити в роботу. Наведені формули є математичним вираженням другого начала термодинаміки: неможливий механізм, який би всю отриману від нагрівача кількість теплоти повністю переводив у роботу (вічний двигун другого роду); частина цієї теплоти повинна бути віддана холодильнику.

У 1865 році Рудольфом Клаузіусом було вперше введено поняття ентропії. Він визначив зміну ентропії термодинамічної системи при оборотному процесі як відношення загальної кількості теплоти ΔQ, отриманої або втраченої системою, до величини абсолютної температури T:

. (6.16)

Клаузіус дав величині S назву «ентропія», утворивши її від грецького слова τρoπή (зміна, перетворення).

Рівність відноситься саме до зміни ентропії. У термодинаміці ентропія визначається лише з точністю до сталої.

Зв'язок між теплоємністю та ентропією дається формулою

. (6.17)

У 1877 році, Людвіг Больцман зрозумів зв’язок між ентропією системи та кількістю можливих «мікростанів», якими може реалізуватися макроскопічний стан із заданими властивостями. Розглянемо, наприклад, ідеальний газ у посудині. Мікростан визначений як положення та імпульси кожного атома, з яких складається система. Братимемо до уваги тільки ті мікростани, для яких: 1) розташування всіх частинок не виходить за межі посудини, 2) загальна енергія газу, що визначається як сума кінетичних енергій атомів, дорівнює певній величині. Больцман постулював що

. (6.18)

де константа k =1,38·10^-23 Дж/К відома тепер як стала Больцмана, а є числом мікроскопічних станів, можливих у заданому макроскопічному стані. Цей постулат, відомий як принцип Больцмана, може розцінюватися, як початок статистичної механіки, яка описує термодинамічні системи, використовуючи статистичну поведінку компонентів, із яких вони складаються. Принцип Больцмана зв'язує мікроскопічні властивості системи (Ω) з однією з її термодинамічних властивостей (S).

Згідно з визначенням Больцмана, ентропія є функцією стану. Більш того, оскільки (Ω) може бути тільки натуральним числом (1,2,3.), ентропія повинна бути додатною – виходячи з властивостей логарифма.

Ентропія є екстенсивною величиною (залежить від маси і об’єму системи), тому сумарна ентропія двох систем

. (6.19)

Якщо друге начало термодинаміки тісно пов’язане з ім’ям Людвіга Больцмана, так третє начало пов’язують з ім’ям німецького фізика й хіміка Вальтера Нернста. Аналізуючи поведінку тіл при низьких температурах поблизу абсолютного нуля, Нернст сформулював теорему, яка має назву теплового закону Нернста або теореми Нернста і стала основою третього начала термодинаміки :

При прямуванні температури до абсолютного нуля зміна ентропії прямує до деякої кінцевої межі, яка не залежить від значень параметрів, що визначають рівноважний стан системи.

Т

обто межа, до якої прямує

не залежить від кінцевого стану системи. Нернст стверджував, що переходи від стану 1 у стани 2 поблизу абсолютного нуля абсолютно рівноцінні.

З такого формулювання випливає, що при процеси, що переводять систему із одного рівноважного стану у інший, протікають без зміни ентропії. Це твердження можна записати у вигляді так званого рівняння Нернста:

. (6.20)

Макс Планк постулював, що ентропія усіх тіл незалежно від їх фізико-хімічної природи та індивідуальних властивостей при абсолютному нулеві температури набуває однакового значення, рівного нулеві. Рівняння

(6.21)

називається рівнянням Планка. Воно загальніше, ніж рівняння Нернста, оскільки рівняння Нернста випливає з нього.

Зваживши на рівняння Планка, теорему Нернста можна сформулювати так: при наближенні до абсолютного нуля температури ентропія усіх тіл прямує до нуля.