Тема №5 «Основні положення молекулярно-кінетичної теорії»

1. Термодинамічні параметри. Стан рівноваги.

2. Гази. Закони ідеальних газів. Рівняння стану ідеального газу.

3. Молекулярна маса. Атомна маса.

4. Розміри молекул. Закон Авогадро.

5. Основне рівняння молекулярно-кінетичної теорії газів.

6. Три положення молекулярно-кінетичної теорії газів.

7. Абсолютна або термодинамічна температура.

8. Закон Максвелла розподілу молекул за швидкостями.

9. Внутрішня енергія. Робота газу.

Молекулярна фізика – це розділ фізики, що вивчає фізичні властивості тіл на рівні розгляду їх молекулярної будови. Задачі молекулярної фізики розв’язують методами фізичної статистики, термодинаміки і фізичної кінетики, вони пов’язані з вивченням руху і взаємодії частинок (атомів, молекул, іонів), з яких складаються тіла.

Успіх теорії Ньютона викликав спроби створити інші теорії, які базувалися б на законах руху. Такі спроби призвели до створення кінетичної теорії газів, яка стала першим сформованим розділом молекулярної фізики. Суть цієї теорії полягала в тому, що тиск газу є результатом бомбардувань стінок дрібненькими частинками, «молекулами», газу. В процесі розвитку кінетичної теорії газів наприкінці XIX століття завдяки роботам Дж. Максвелла, Л. Больцмана, Дж. Гіббса була створена класична статистична фізика. Приблизно в той же час в теорії капілярних явищ почали розвиватися кількісні уявлення про взаємодію молекул, чому сприяли роботи К.Клеро, П.Лапласа, Т.Юнга, К.Гаусса. Міжмолекулярні взаємодії були враховані Й.Ван-дер-Ваальсом при поясненні фізичних властивостей реальних газів та рідин.

На початку ХХ століття молекулярна фізика вступила в новий етап розвитку. Роботи Ж. Перрена, Т. Сведберга, М. Смолуховського і А. Ейнштейна, присвячені броунівському рухові, довели існування молекул. Методами рентгеноструктурного аналізу, а пізніше – методами електронографії та нейтронографії були вивчені структурні особливості твердих тіл та рідин, їх зміна при здійсненні фазових переходів, зміні температури, тиску та інших характеристик.

Коло питань, які охоплює молекулярна фізика, надзвичайно широкий. Вона розглядає будову речовини та її зміни під дією зовнішніх факторів (тиску, температури, електричного і магнітного полів), явища переносу (дифузію, теплопровідність, в’язкість), фазову рівновагу і процеси фазових переходів (кристалізацію, плавлення, випаровування, конденсацію та ін.), критичний стан речовини, поверхневі явища на границях розділення фаз.

Стан будь-якої речовини чи тіла можна охарактеризувати за допомогою цілого рядку показників чи параметрів. Молекулярна фізика використовує так звані термодинамічні параметри.

Термодинамічні параметри – це величини, що можуть змінюватися зі зміною самої системи внаслідок її взаємодії з навколишнім середовищем. До термодинамічних параметрів належать температура, густина, теплоємність, питомий електричний опір і багато інших фізичних величин.

Термодинамічні параметри можна поділити на основні та допоміжні. До основних термодинамічних параметрів належать такі, які легко визначити простими технічними засобами (тиск, температура, питомий об’єм). Сукупність зазначених основних термодинамічних параметрів визначає стан системи у даний момент.

Важливим поняттям молекулярної фізики є поняття стану термодинамічної рівноваги – це такий стан термодинамічної системи, в який вона переходить впродовж тривалого проміжку часу в умовах ізоляції від зовнішнього середовища. При досягненні стану рівноваги в системі припиняються всі незворотні процеси, пов’язані з дисипацією³ енергії: теплопровідність дифузія, хімічні реакції та ін. в стані термодинамічної рівноваги параметри системи не змінюються з часом, хоча, якщо говорити строго, то ті з параметрів, які не фіксують задані умови існування системи, можуть мати флуктуації – незначні коливання відносно своїх середніх значень. Як правило, ізоляція здійснюється за допомогою нерухомих стінок, непроникних для речовини. Якщо стінки не проводять теплоти (наприклад, в посудині Дьюара), то ізоляція називається адіабатичною. При теплопровідних (діатермічних) стінках між системою й зовнішнім середовищем можливий обмін теплообмін до встановлення стану термодинамічної рівноваги. Перехід системи в рівноважний стан називають релаксацією.

Агрегатний стан речовини, в якому атоми в молекули, з яких вона складається, майже вільно й хаотично рухаються у проміжках між зіткненнями, при яких відбувається різка зміна характеру їх руху, називається газом. Слід зазначити, що в газах час вільного руху молекул значно перевищує час їх зіткнення. На відміну від рідин гази не утворюють вільної поверхні й рівномірно заповнюють увесь доступний об’єм.

За хімічними властивостями гази та їх суміші надзвичайно різноманітні – від малоактивних інертних газів до вибухових газових сумішей. Газами інколи називають не тільки системи з атомів і молекул, але й системи інших частинок – фотонів, електронів, броунівських частинок, а також плазму.

Газ називають ідеальним, якщо для нього можна знехтувати розмірами молекул та силами молекулярної взаємодії. Молекули в такому газі взаємодіють за законами пружної взаємодії тіл. Реальні гази поводять себе як ідеальні при значному їх розрідженні.

Процеси, які відбуваються в газі при сталому значенні одного з термодинамічних параметрів(Т, V або p), називаються ізопроцесами.

При сталій температурі в газі відбувається процес, який називають ізотермічним. Згідно із законом Бойля-Маріотта, тиск даної маси газу при сталій температурі обернено пропорційний об’єму газу:

або . (5.1)

Криву залежності тиску газу від його об’єму при сталій температурі називають ізотермою. Графік залежності між параметрами газу при Т = const має вигляд:

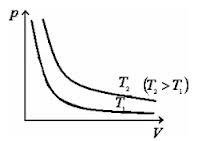
Ізобаричний процес – процес, який відбувається при сталому тиску (р = const). Виходячи із закону Гей-Люссака, відносна зміна об’єму даної маси газу в ізобарному процесі прямо пропорційна зміні температури Т:

або або . (5.2)

де V₀ – об’єм газу при Т = 0^оС, V – його об’єм при температурі Т, α – термічний коефіцієнт об’ємного розширення. Для всіх газів .

Криву залежності об’єму газу від температури при сталому тиску називають ізобарою. Графік залежності між параметрами при р= const:

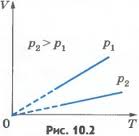
Вищому тиску відповідає нижча ізобара. Штрихи означають, що закон Гей-Люссака в області низьких температур не застосовується. Об’єм не може перетворитися в нуль при температурі -273 ⁰С.

Ізохоричний процес – це процес, який відбувається при сталому об’ємі (V = const). Виходячи із закону Шарля, тиск даної маси газу при сталому об’ємі пропорційний його абсолютній температурі:

або , (5.3)

де р₀ – тиск при 0⁰С, α – термічний коефіцієнт тиску газу.

Залежність тиску газу від температури при сталому об’ємі графічно зображується прямою, яка називається ізохорою. Меншому об’ємові відповідає ізохора, що лежить вище. Графік залежності між параметрами при сталому об’ємі V = const:

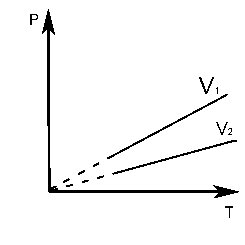
Температуру -273,16С називають абсолютним нулем температур.

Англійський вчений У.Томсон запропонував абсолютну шкалу температур. За абсолютний нуль було прийнято температуру t = -273C (точніше, t₀ = -273,16С) абсолютна температура Т пов’язана з температурою t за шкалою Цельсія таким співвідношенням :

. (5.4)

В шкалі Цельсія за 0С прийнято температуру танення льоду при нормальному тискові, за 100С – температуру кипіння води при нормальному тискові.

В шкалі Кельвіна за 0 прийнято температуру, при наближенні до якої швидкість поступального руху молекул ідеального газу прямує до нуля, а 1 кельвін відповідає 1/100 інтервалу температур між температурами танення льоду і кипіння води за нормального тиску.

За шкалою Фаренгейта:

. (5.5)

Основна одиниця температури в СІ є Кельвін [Т] = К.

Змінюючи всі три параметра р, V і Т газу і користуючись газовими законами, можна отримати рівняння Клапейрона:

. (5.6)

Добуток тиску даної маси газу на об’єм, поділений на абсолютну температуру, є величиною сталою.

При t = 0C, р = 1,013^.10⁵Па один моль будь-якого газу має об’єм V₀=22,4^.10^-3м³. Підставивши ці дані в закон Клапейрона, отримуємо значення константи, яка є однакова для будь-якого 1 моля газу. Її називають молярною універсальною газовою сталою:

. (5.7)

Для одного моля газу тепер можна записати:

. (5.8)

Цей вираз називають рівнянням Менделєєва – Клапейрона.

А для будь-якої маси газу рівняння Менделєєва – Клапейрона матиме вигляд:

. (5.9)

Якщо в об’ємі V знаходиться суміш газів, які не реагують один з одним, то, використавши рівняння Менделєєва – Клапейрона, визначимо тиск:

, (5.10)

де т_і, _і – маса і молярна маса і-того газу.

Закон Дж. Дальтона: Тиск суміші газів дорівнює сумі парціальних тисків газів, з яких складається дана суміш.

Парціальним тиском називається тиск, який був би створений за даних умов (Т,V) окремо одним газом з суміші.

У 1811 році італійським фізиком Амедео Авогадро був відкритий закон, згідно з яким однакові об’єми будь-яких газів при однаковому тиску і температурі містять однакову кількість молекул. Цей закон назвали законом Авогадро. Як наслідок закону Авогадро, можна сформулювати твердження про те, що однакові кількості молекул різних газів при однаковій температурі і однаковому тиску займають однакові об’єми.

Оскільки 1 моль⁴ будь-яких газів містить однакову кількість молекул – 6,02^.10²³, це число називають сталою Авогадро і позначають N_A.

Об’єм, який займає один моль будь-якого газу при нормальних умовах, називається молярним об'ємом (позначається V_m). Нормальними (скорочено н.у.) називаються такі умови, коли температура дорівнює 0°C, а тиск 1 ат., або 760 мм рт.ст. Молярний об’єм усіх газів незалежно від їх маси однаковий і дорівнює 22,4 дм³ (22,4 л).

Молекула – це найдрібніша частинка речовини, яка може існувати окремо, зберігаючи при цьому властивості речовини. Руйнування будь-якої молекули означає втрату відповідних властивостей.

Д ля більшості газів молекули складаються з двох-трьох атомів, або й зовсім з одного (гелій, неон). Та є й такі, що містять кілька тисяч атомів, поєднаних у певній послідовності. Наприклад, молекула чистого каучуку складається приблизно з 75 тис. атомів вуглецю і 100 тис. атомів водню. Отже, розмір молекули – поняття достатньо широке. Якщо молекула води має розмір у мільярдну частку сантиметра, то розмір тієї ж молекули гуми в тисячі разів більший. Або: в 10 см³ льоду міститься більше ніж 300 мільйонів мільярдів молекул (3^.10²⁰). При цьому варто пам’ятати, що значну частину такого кубика льоду займає вільний простір.

Взагалі кажучи, розмір молекули, тобто розмір її електронної оболонки, є величиною до певної міри умовною. Існує ймовірність (хоча й дуже мала) знайти електрони молекули і на більшій відстані від її атомного ядра. Практичні розміри молекули визначаються рівноважною відстанню, на яку вони можуть бути зближені при щільному упакуванні молекули в молекулярному кристалі та в рідині. На великих відстанях молекули притягаються одна до одної, на менших – відштовхуються. Розміри молекули можна знайти за допомогою рентгеноструктурного аналізу молекулярних кристалів. Порядок величини цих розмірів може бути визначений з коефіцієнтів дифузії, теплопровідності та в’язкості газів та з густини речовини в конденсованому стані. Відстань, на яку можуть зблизитись валентно не зв’язані атоми однієї й тієї ж чи різних молекул, може бути охарактеризована середніми значеннями так званих ван-дер-Ваальсових радіусів (Ǻ).

Молекулярно-кінетична теорія виходить з того положення, що речовина, зокрема, газ, складається з величезної кількості молекул чи атомів, які, рухаючись хаотично і стикаючись між собою та зі стінками посудини, здійснюють на них тиск. Всі зіткнення вважаються пружними, тобто проходять без втрати енергії. Середня кінетична енергія руху таких частинок залежить від температури.

Середня кінетична енергія руху молекули дорівнює:

, (5.11)

де m – маса частинки, v – її швидкість, k – стала Больцмана, Т – температура.

Середня швидкість частинок у газі дорівнює:

, (5.12)

де R – газова стала, μ – молярна маса.

Врахувавши той факт, що при пружному ударі об стінку зміна імпульсу частинки дорівнюватиме 2mv_x, де v_x – перпендикулярна до стінки складова швидкості, можна отримати рівняння для тиску

, (5.13)

де n – кількість частинок в одиничному об’ємі. Вираз (5.13) називають основним рівнянням молекулярно-кінетичної теорії газів.

Основні положення МКТ речовини:

I. Будь-які речовини мають дискретну (переривчасту) будову. Вони складаються з найдрібніших частинок молекул і атомів.

II. Молекули знаходяться в стані неперервного хаотичного (невпорядкованого) руху, що називається тепловим і у загальному випадку є сукупністю поступального, обертального і коливального рухів.

III. Молекули взаємодіють одна з одною із силами електромагнітної природи, причому на великих відстанях вони притягуються, а на малих – відштовхуються. Сили притягання і відштовхування між молекулами діють постійно.

Внаслідок безперервного хаотичного руху молекул, а також взаємного зіткнення молекул під час цього руху кожна молекула зокрема може змінювати свою швидкість як за величиною, так і за напрямком. Тому в газі будуть як швидкі, так і повільні молекули. Але, хоча швидкості окремих молекул змінюються, властивості газу у стані термодинамічної рівноваги загалом при цьому не змінюються: залишаються постійними параметри системи. Зумовлено це тим, що швидкості газових молекул підлягають певному законові, тобто, незважаючи на повну хаотичність молекулярних рухів, розподіл молекул за швидкостями виявляється не випадковим, а цілком визначеним. До того ж він є однозначним і єдино можливим.

Дж. Максвелл теоретично розв’язав задачу про розподіл молекул ідеального газу за швидкостями поступального руху. Він встановив закон, що дає змогу визначити, яка кількість молекул dn із загальної кількості n молекул ідеального газу в одиниці об’єму мають при даній температурі швидкості, які лежать в інтервалі від v до v + dv. Максвелл вважав, що газ складається з великої кількості однакових молекул, температура в усіх частинах посудини з газом теж однакова і відсутні зовнішні дії на газ.

Закон Максвелла описується деякою функцією f(v), що називається функцією розподілу молекул за швидкостями руху. Ця функція визначає відносну кількість молекул , швидкості яких лежать в інтервалі від v до v + dv.

Застосовуючи методи теорії імовірності, Максвелл знайшов функцію f(v) у такому вигляді:

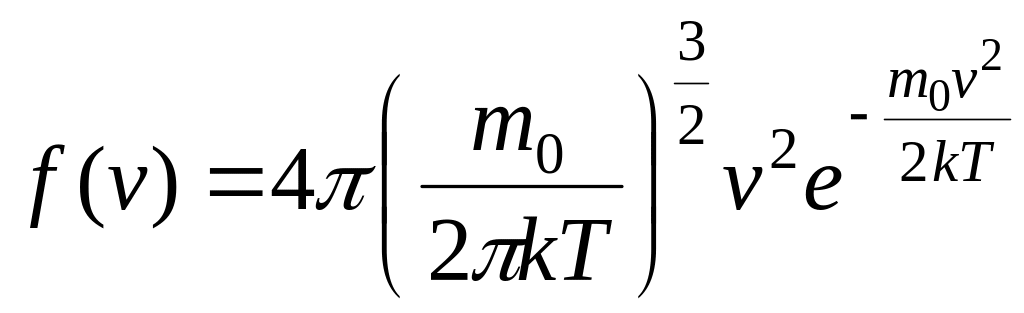. (5.14)

Конкретний вигляд функції залежить від роду газу і його параметрів. Графік функції наведений на рисунку:

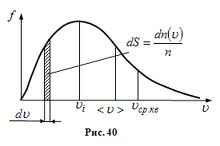
Як видно з графіка, функція несиметрична відносно максимального значення.

Виходячи з графіка розподілу, є три швидкості, які характеризують стан газу:

, (5.15)

яку називають найімовірнішою;

, (5.16)

яку називають середньою арифметичною;

, (5.17)

яку називають середньою квадратичною.

Оскільки в ідеальному газі відсутні сили взаємодії, то це означає, що молекулярно-потенціальна енергія у нього відсутня. Отже, внутрішня енергія ідеального газу представляє собою тільки суму значень кінетичних енергій хаотичного руху всіх його молекул.

, де . (5.18)

Для одного моля внутрішня енергія буде виражена формулою:

, (5.19)

а для довільної маси одноатомного газу

. (5.20)

Стискуючи газ, ми виконуємо роботу, а під час розширення газу він сам буде виконувати роботу:

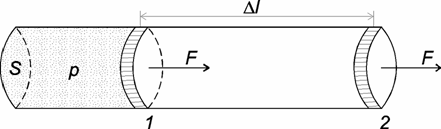
Якщо газ нагріти від Т₁ до Т₂, то тиск газу збільшиться і поршень переміститься з положення 1 в положення 2 на відстань в результаті виконаної газом роботи проти зовнішніх сил.

Сила, яка виконує цю роботу, дорівнює добутку тиску на площу. Оскільки – це зміна об’єму, то маємо 

або .

Газ виконує роботу тільки тоді, коли є зміна об’єму.

Виходячи з поняття роботи ідеального газу, можна так сформулювати зміст уведених раніше констант:

а) універсальна газова стала чисельно дорівнює роботі, яку виконує моль ідеального газу при його ізобаричному нагріванні на 1 Кельвін:

; (5.21)

б) стала Больцмана показує, скільки роботи припадає в середньому на одну молекулу ідеального газу при ізобаричному нагріванні на один Кельвін:

. (5.22)