25. Баланс энергий в скважине. Классификация способов добычи нефти

W_П+W_Н=W₁+W₂+W₃

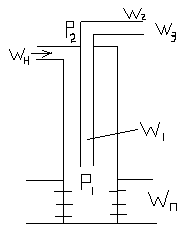
W_П – энергия пласта, W_Н – энергия подаваемая с поверхности

W₁ - энергия затрачиваемая на подъем жидкости и газа с забоя до устья

W₂ – энергия расходуемая газожидкостной смесью при движении через устьевое оборудование

W₃ – энергия уносимая потоком за пределы устья скважины

На забое жидкость и газ обладают потенциальной энергией. Количество этой энергии определяется энергией жидкости и газа. Потенциальная энергия затрачивается для совершения работы по подьему жидкости на некоторую высоту h от забоя скважины. Отсюда W_Ж=ρgh. Если высоту подъема жидкости выразить через забойное давление то получим:

, тогда W_Ж=Р_С-Р₀ . Энергия свободного газа , Г₀ – объем газа поступившего к забою скважины в свободном виде с одной тонной жидкости. При давлении равном Р_с в каждой тонне нефти содержится какое то количество растворенного газа которое будет выделено из жидкости по мере приближения к устью. Этот газ так же обладает некоторым запасом энергии W_П =W_Ж+W_Г+W₀ . Но эта энергия не вся используется для подъема жидкости т.к. на устье создается некоторое противодавление Р₂. Тогда энергия W₁ расходуется на подъем жидкости при изменении давления от Р_с до Р₂ будет учитываться с добавлением энергии газа выделившегося из нефти от от Р_с до Р₂.

Способы добычи. При эксплуатации фонтанных скважин давление на забое бывает выше давления насыщения нефти и газа. При этом Г₀=0 и подъем жидкости происходит за счет энергии жидкости и энергии выделившегося в стволе скважины газа. Для фонтанных скважин справедливо условие W_П >W₁+W₂+W₃. При наличии энергии подаваемой с поверхности, будет уже механизированная эксплуатация скважины.

Классификация:

1 фонтанные подъемники W_H=0

2 Механизированные способы W_H>0

2.1 механические

2.2 компрессорные

26. Подъем жидкости за счет энергии расширяющегося газа

Проведем опыт.

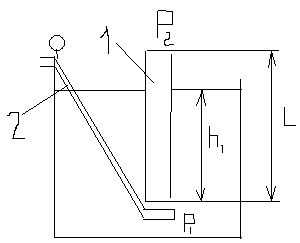
Представим, что трубка 1 длинною L погружена под уровень жидкости не ограниченного объема на глубину h. К нижнему открытому концу трубки подведена другая трубка 2 для подачи с поверхности сжатого газа. Давление у башмака 1 равно гидростатическому на глубине h, т.е. Р₁ не зависит от количества подаваемого газа. Если по указанной схеме за счет подачи газа в подъемнике происходит подъем жидкости от башмака с давлением Р₁ до устья Р₂, то этот процесс можно описать уравнением: Р₁-Р₂+Р_ТР=0. При условии, что Q_Ж>0 и преобразовав, уравнение примет вид: , - градиент напора газожидкостного подъемника. Из этого уравнения видно, что эффективность подъема жидкости за счет энергии расширяющегося газа зависит от градиента напора подъемника и плотности газожидкостной смеси в подъемнике. Для эффективного подъема жидкости необходимо создавать условия для получения наибольших значений градиента напора и наименьших значений плотности смеси.