
- •2.2. Нелинейный метод формирования ам-сигналов.
- •2.2.1. Статическая модуляционная характеристика
- •2.2.3. Добротность контура и спектр выходного напряжения
- •3. Теория и решение задачи . 2
- •3.1. Сигналы угловой модуляции и их свойства
- •3.2 Принцип формирования чм-сигналов и принципиальная схема частотного модулятора.
Таким образом, общее выражение АМ-сигнала при модуляции по закону х(t) есть
![]() (2)
(2)
2.1.2. Спектр периодической модулирующей функции и спектр АМ-cигнала
Е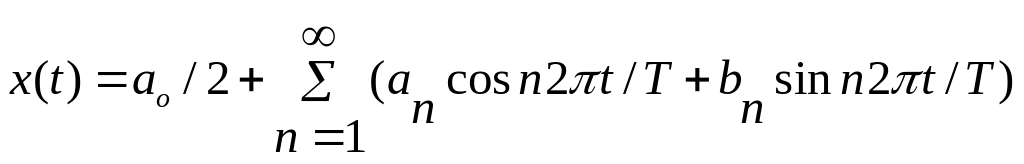 сли
х(t)
-
периодическая, периода Т, функция, то
ee
можно
записать в виде ряда Фурье:
сли
х(t)
-
периодическая, периода Т, функция, то
ee
можно
записать в виде ряда Фурье:
(3)
где-![]() ,
,
![]() -коэффициенты
Фурье, вычисленные по формулам:
-коэффициенты
Фурье, вычисленные по формулам:
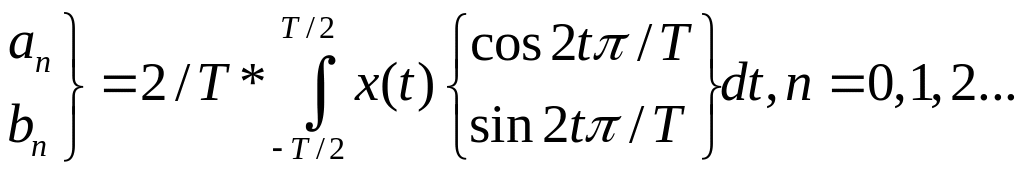
(4)
В (4) под интегралом нужно брать функцию, стоящую в соответствующей строке (т.е. для аn – cos, bn -sin).
Вводя
в рассмотрение амплитуду
Сп
и
фазу
![]() ,
n-ой
гармоники,
,
n-ой
гармоники, ![]()
![]() (5)
(5)
можно ряд (3) записать в эквивалентной форме:
![]()
(6)
Подставляя это последнее выражение в (2), получим запись АМ- сигнала, из которой ясен его частотный состав:
![]()
![]() (7)
(7)
Здесь первое слагаемое - несущее колебание, а суммы - соответственно нижняя и верхняя боковые полосы спектра АМ-сигнала.
2.1.3. Эффективная протяжённость спектра модулирующей функции и АМ-колебания
В
суммах (6) и (7) фигурирует бесконечное
число слагаемых, так что спектр
функции х(t)
и спектр АМ-сигнала с законом модуляции
х(t)
формально
имеют неограниченную протяжённость
по оси частот. Однако для любого
физического сигнала х( t
) его
ряд Фурье обладает тем свойством, что
![]() при
при
![]() ,
хотя,
возможно, и не монотонно. Если задать
некоторое
,
хотя,
возможно, и не монотонно. Если задать
некоторое
![]() (например,
в виде
(например,
в виде
![]() ;
где
;
где
![]() -размах
х( t
),
a
-размах
х( t
),
a
![]() ),то
всегда можно указать такое
),то
всегда можно указать такое
![]() начиная
с которого все
начиная
с которого все
![]() оказываются
меньше
, т.е.
оказываются
меньше
, т.е.
![]() если
если
![]() (8)
(8)
Тогда условно можно считать, что
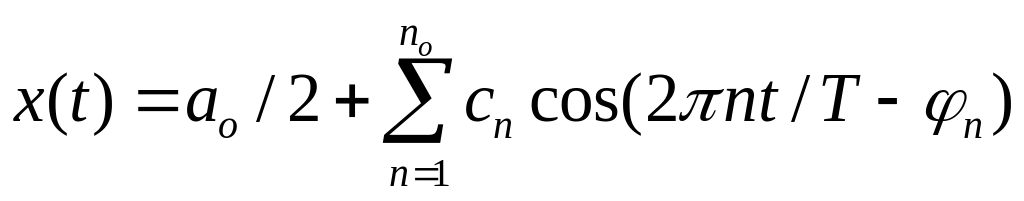 (9)
(9)
с ошибкой порядка . Обычно = (0,01 - 0,I) ,
Число nо гармоник функции х( t ), найденное с учётом (8), определяет эффективную ширину (или протяжённость) спектра этой функции:
![]() (10)
(10)
Здесь
![]() -основная
круговая частота функции х( t
).
-основная
круговая частота функции х( t
).
Из (10), (9) и (7) следует, что спектр АМ-сигнала при модуляции периодической функцией х( t ) имеет эффективную ширину
![]() (11)
(11)
с
крайними частотами
![]()
2.2. Нелинейный метод формирования ам-сигналов.
В
принципиальном отношении сущность AM
сводится к перемножению функций х( t
)
и
![]() .
В силу целого ряда причин это перемножение
в подавляющем большинстве случаев
осуществляется косвенным путём, за счёт
использования свойств нелинейных цепей.
.
В силу целого ряда причин это перемножение
в подавляющем большинстве случаев
осуществляется косвенным путём, за счёт
использования свойств нелинейных цепей.
Принцип
формирования AM
в нелинейной цепи основан на том, что
при воздействии суммы U=
х( t
) +
на
нелинейный элемент с вольтамперной
характеристикой (ВАХ) вида
![]() в
отклике y
(t)
появляется
компонента вида
в
отклике y
(t)
появляется
компонента вида
![]() .
.
Принципиальная схема амплитудного модулятора с транзистором в качестве нелинейного элемента изображена на рис.1.
В этой схеме используется нелинейность коллекторно-базовой ВАХ транзистора iK=iK(UБ) называемой также характеристикой прямой передачи).
К базе транзистора приложено 2 напряжения – высокочастотное Ucosωot и
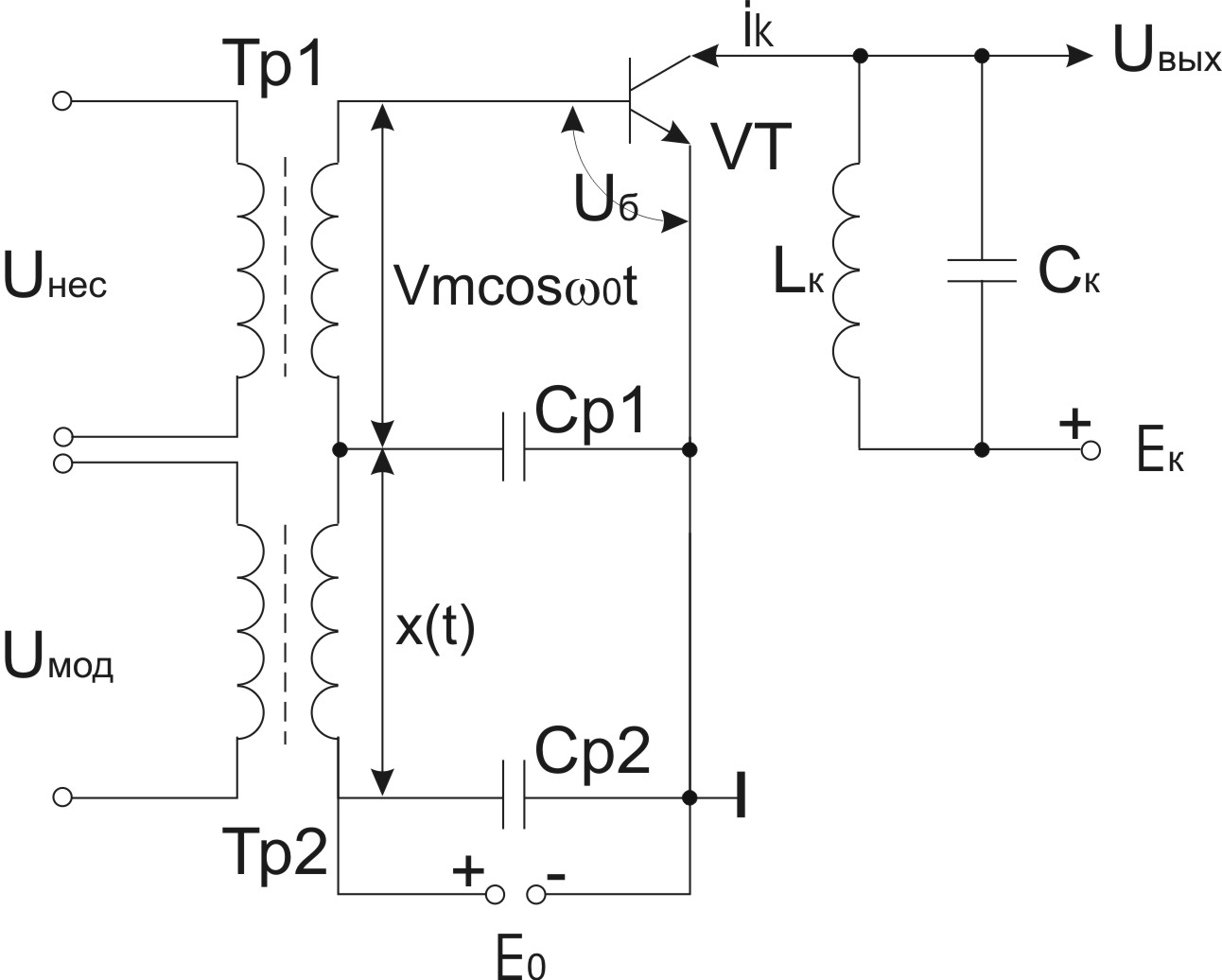
Рисунок 1
низкочастотное
![]()
Контур
в коллекторной цепи настроен на частоту
![]() , так что напряжение Uвых(
t
)
создаётся практически только
теми компонентами тока
i
(t
),
частоты
которых попадают в небольшую окрестность
частоты
, так что напряжение Uвых(
t
)
создаётся практически только
теми компонентами тока
i
(t
),
частоты
которых попадают в небольшую окрестность
частоты
![]() ,
определяемую
полосой пропускания контура.
,
определяемую
полосой пропускания контура.
При
модуляции напряжение
Е(t)
изменяет
положение мгновенной рабочей точки
для колебания
![]() как
следствие
изменяется
средняя крутизна Sср
для
первой гармоники частоты U)Q
и
амплитуда
как
следствие
изменяется
средняя крутизна Sср
для
первой гармоники частоты U)Q
и
амплитуда
![]() этой гармоники коллекторного тока.
этой гармоники коллекторного тока.
Если
в схеме на рис.1 в качестве нелинейного
элемента используется иной прибор
(электронная лампа или полевой
транзистор), то ни схема, ни физика
процессов в ней, ни метод расчёта не
изменяются; единственно, что меняется
- это используемая при расчёте
зависимость тока от напряжения; в случае
ЭВ-прибора используется зависимость
![]() (анодно-сеточная
характеристика), в случае полевого
транзистора - зависимость
(анодно-сеточная
характеристика), в случае полевого
транзистора - зависимость
![]() (сток-затворная характеристика).
(сток-затворная характеристика).
2.2.1. Статическая модуляционная характеристика
Инженерный расчёт амплитудного модулятора по схеме на рис.1 основан на понятии статическ ой модуляционной характеристики, вводимом следующим образом.
Пусть
Е( t
) =
Е (т.е. не изменяется во времени). Тогда
![]() ,
а ток в цепи коллектора –
,
а ток в цепи коллектора –
![]()
где![]() ...
- амплитуды гармоник этого тока. Эти
амплитуды зависят как от
...
- амплитуды гармоник этого тока. Эти
амплитуды зависят как от
![]() так
и от Е.
так
и от Е.
Семейством
статических модуляционных характеристик
называется зависимость амплитуды
первой гармоники
![]() ,
рассматриваемая как функция 2-х
переменных -
и
Е:
,
рассматриваемая как функция 2-х
переменных -
и
Е:
![]()
Если
в этой зависимости принять vm=
const,
то
получим какую-то одну модуляционную
характеристику:![]() (Заметим,
что при Е =const
зависимость
(Заметим,
что при Е =const
зависимость
![]() есть
колебательная характеристика, лежащая
в основе квазилинейного метода
исследования стационарного режима
генератора синусоидальных колебаний).
есть
колебательная характеристика, лежащая
в основе квазилинейного метода
исследования стационарного режима
генератора синусоидальных колебаний).
Метод
вычислений модуляционной характеристики
непосредственно вытекает из её
определения: нужно в зависимость![]() подставить
подставить
![]() ,а
затем найти I,
как явную функцию Е при данном
.
При
аналитическом расчёте необходимо
предварительно аппроксимировать
графически заданную ВАХ сквозной
передачи
,а
затем найти I,
как явную функцию Е при данном
.
При
аналитическом расчёте необходимо
предварительно аппроксимировать
графически заданную ВАХ сквозной
передачи
![]() .
Способ
аппроксимации выбирают с учётом как
исходных условий, так и реальной
зависимости
.
Способ
аппроксимации выбирают с учётом как
исходных условий, так и реальной
зависимости
![]() ,
именно,
если заданная амплитуда
мала
по сравнению с протяжённостью начального,
существенно нелинейного участка ВАХ
сквозной передачи, то следует применять,
как правило, полиномиальную аппроксимацию;
если
велико (так что коллекторная цепь
работает в режиме отсечки), то целесообразно
использовать кусочно-линейную
аппроксимацию.
,
именно,
если заданная амплитуда
мала
по сравнению с протяжённостью начального,
существенно нелинейного участка ВАХ
сквозной передачи, то следует применять,
как правило, полиномиальную аппроксимацию;
если
велико (так что коллекторная цепь
работает в режиме отсечки), то целесообразно
использовать кусочно-линейную
аппроксимацию.
Приводимые ниже примеры поясняют метод расчёта модуляционной характеристики.
Пример I.
![]()
Пусть на интервале зависимость передаётся полиномом 3-ей степени:
![]()
Найти модуляционную характеристику, Решение. Имеем:
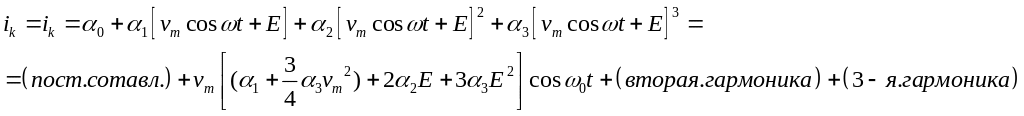
Таким образом
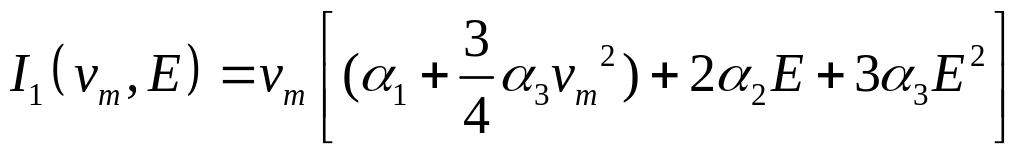
(12)
или иначе,
(![]() 13)
13)
г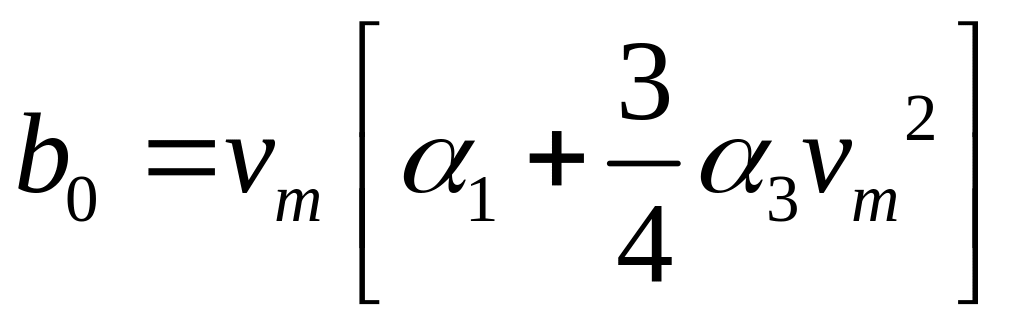
![]() де
де
![]() (14)
(14)
Так
как, по исходному предположению, ВАХ
описывается полиномом лишь на интервале
Uбmin≤Uб≤Uбmax,
то полученные соотношения (12), (13)
правомерно использовать лишь при тех
значениях Е, которые не выводят напряжение
Uб
за границы этого интервала. Другими
словами, в (12) и (13) можно подставлять
только
![]()
Пример 2.
Пусть ВАХ транзистора передаётся функцией вида:
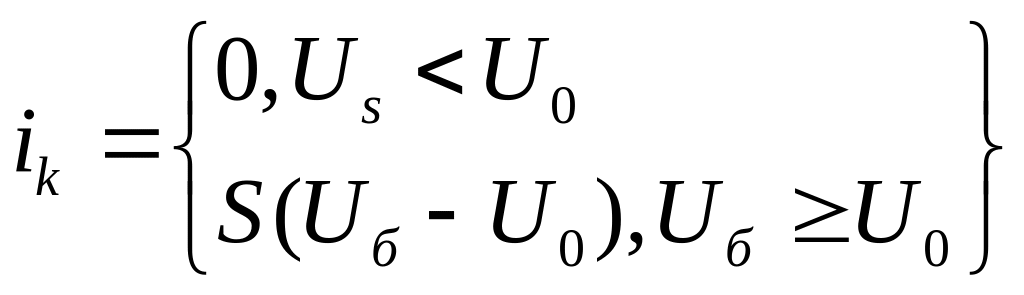
(15)
Найти модуляционную характеристику.
Решение.
П![]() одставляя
в (15) и используя стандартные
выкладки метода угла отсечки, можно
записать:
одставляя
в (15) и используя стандартные
выкладки метода угла отсечки, можно
записать:
(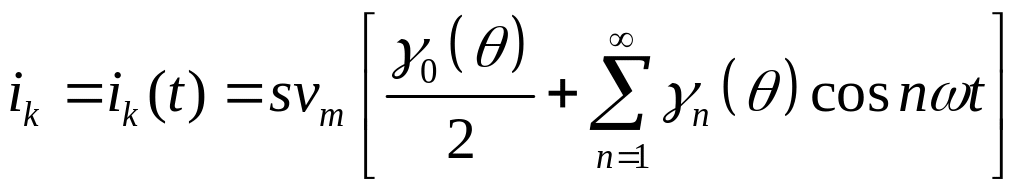 16)
16)
где
![]() - гамма-коэффициент
Берга,
- гамма-коэффициент
Берга,
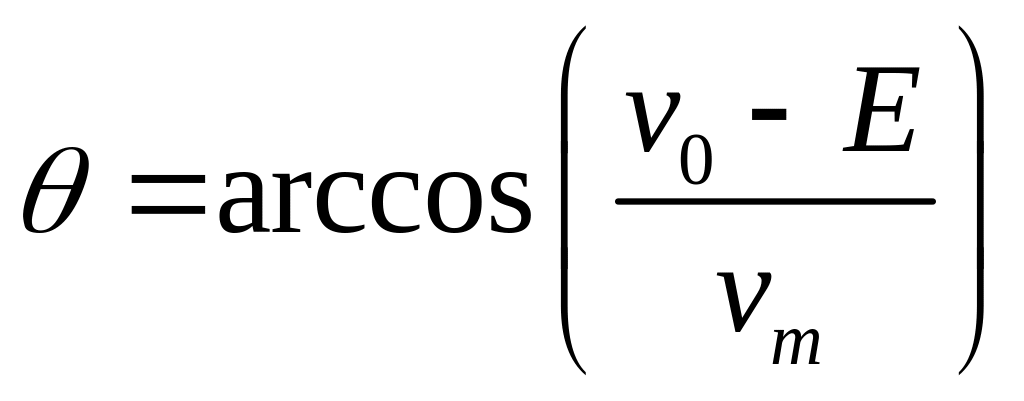
для легко получить следующее выражение:
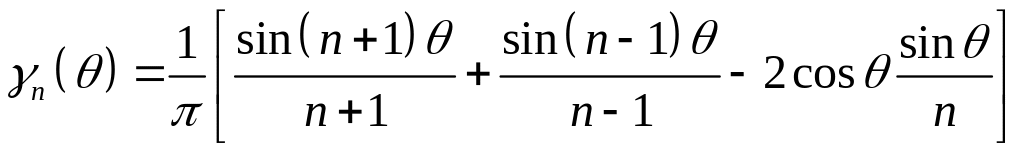
Подставляя сюда n =1, выполняя несложные преобразования и имея в виду (16), можно получить следующее общее выражение для модуляционной характеристики при работе в режиме с отсечкой тока:
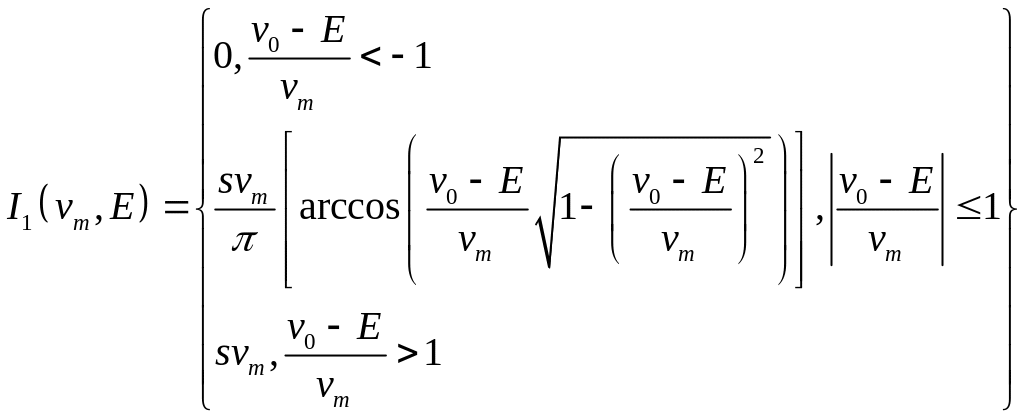
(17)
2.2.2. Выбор рабочей точки на модуляционной характеристике и расчёт нелинейных искажений модуляции
Рабочая
точка (напряжение Е![]() и соответствующее ему значение I
и соответствующее ему значение I![]() ) выбирается
на середине линейного (или почти
линейного) участка модуляционной
характеристики с таким расчётом,
чтобы обеспечить наибольший допустимый
размах ∆Е напряжения модуляции и,
соответственно, наибольшую величину
∆I
абсолютного
прироста амплитуды тока первой г
) выбирается
на середине линейного (или почти
линейного) участка модуляционной
характеристики с таким расчётом,
чтобы обеспечить наибольший допустимый
размах ∆Е напряжения модуляции и,
соответственно, наибольшую величину
∆I
абсолютного
прироста амплитуды тока первой г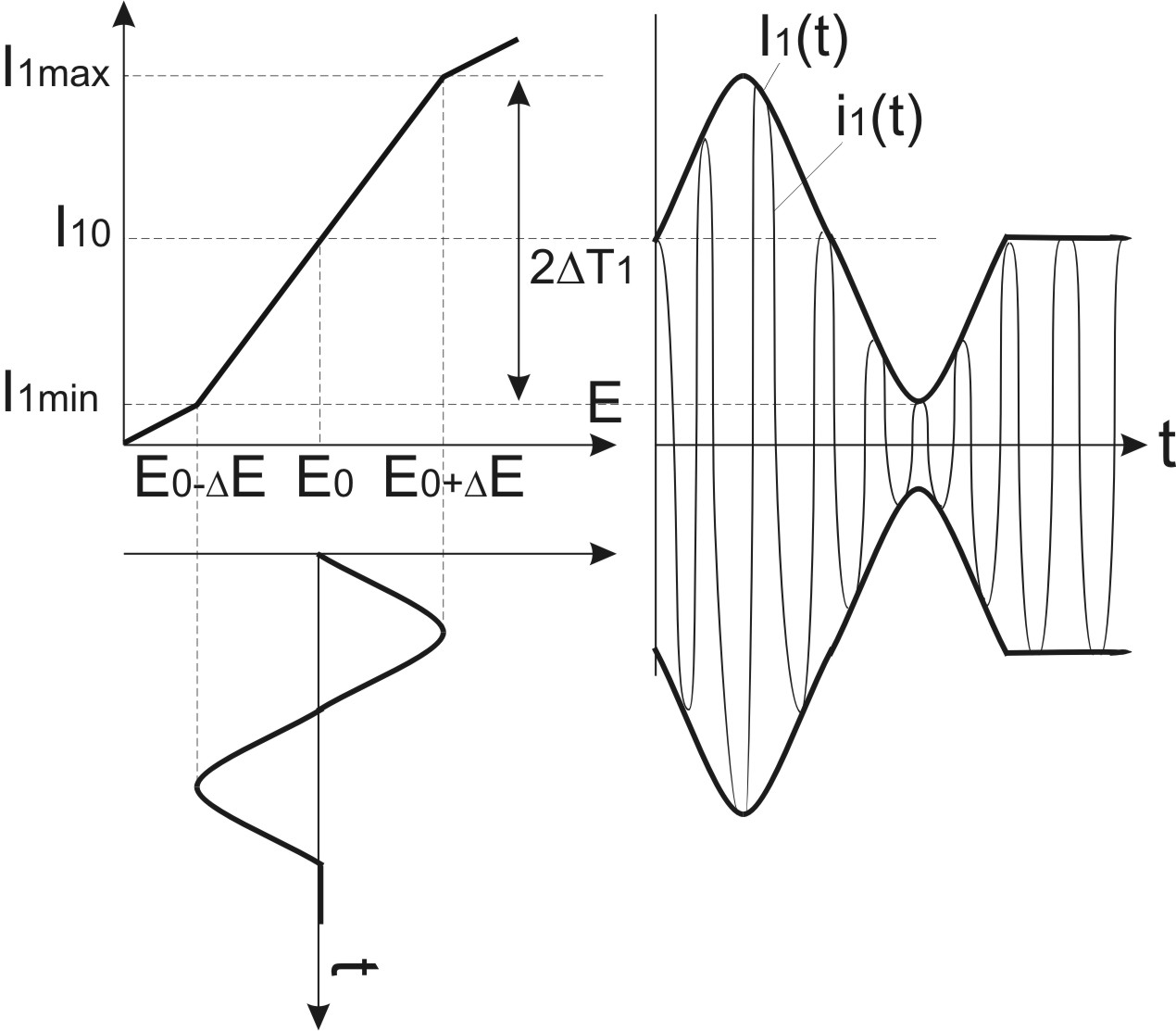 армоники
(см.рис. 2).
армоники
(см.рис. 2).
Рисунок 2
Качество модуляции принято характеризовать величиной нелинейных скажений огибающей, возникающих при модуляции по гармоническому закону, т.е. при
Если
модуляционная характеристика
в
пределах рабочего участка
![]() строго линейна, то
строго линейна, то
![]() где k
- её наклон в точке Ео.
где k
- её наклон в точке Ео.
Если
модуляционная характеристика нелинейна,
то амплитуда
![]() уже не повторяет точно закон изменения
Е(t);
в огибающей АМ-колебания появляются
гармоники частоты модуляции Ω.
уже не повторяет точно закон изменения
Е(t);
в огибающей АМ-колебания появляются
гармоники частоты модуляции Ω.
![]()
Количественной мерой искажений служит коэффициент гармоник Кг:
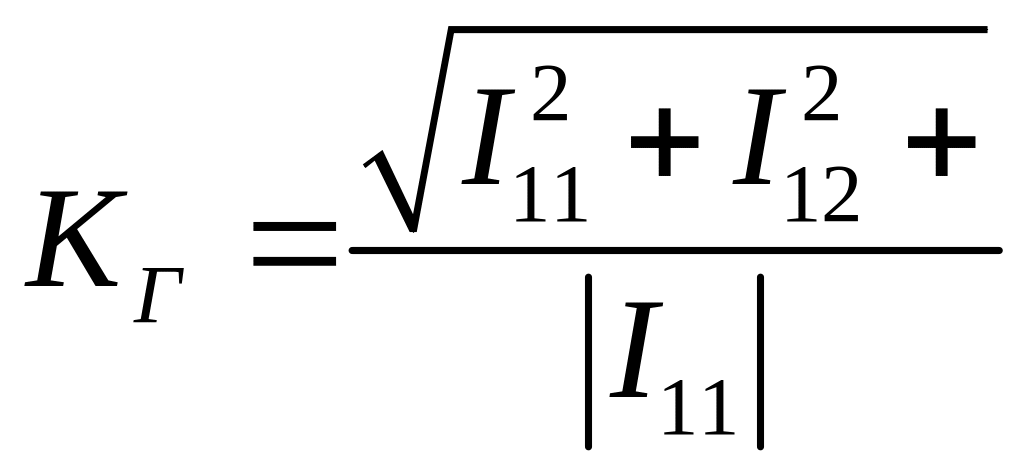
(18)
Амплитуды
![]() гармоник огибающей могут быть найдены
либо непосредственно (если
гармоник огибающей могут быть найдены
либо непосредственно (если
![]() описывается
полиномиальной зависимостью), либо
методами приближённого гармонического
анализа (в частности, методом 5-ти
ординат).
описывается
полиномиальной зависимостью), либо
методами приближённого гармонического
анализа (в частности, методом 5-ти
ординат).
Коэффициент
гармоник Кг
(называемый также коэффициентом
нелинейных искажений) зависит от размаха
модулирующего напряжения
![]() или что то же самое, от глубины модуляции
m,
которая при данном
определяется так:
или что то же самое, от глубины модуляции
m,
которая при данном
определяется так:
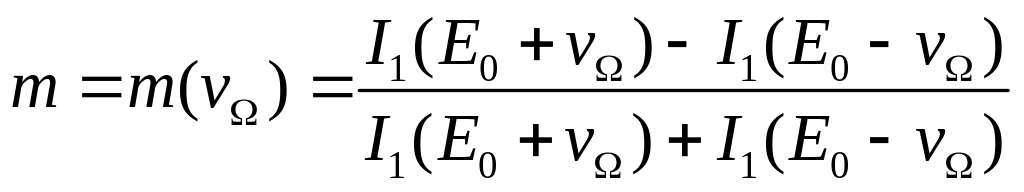 (19)
(19)
Здесь Еo - рабочая точка на модуляционной характеристике.
Чтобы построить зависимость Кг( m ), нужно задаться несколькими (от 3-х до 5-ти) значениями (так, чтобы получить значения т в пределах 0,2≤m≤0.8-0.9 и для каждого найти соответствующие ему Кг и m .
По построенной зависимости легко найти наибольшее значение m и соответствующее ему значение ∆Е, если задано допустимое значение Кг (в условии 1-й задачи допустимое значение Кг≤0,2).
Способ вычисления Кг и m поясняется приводимыми ниже примерами.
Пример 3.
Пусть
модуляционная характеристика описывается
полиномом
![]()
(см. пример I). Найти Кг и m как функции .
Решение.
Полагая![]() ,
имеем:
,
имеем:
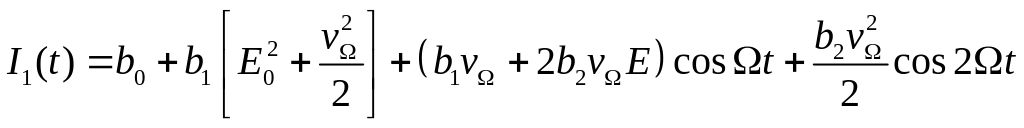
(20)
Таким образом,
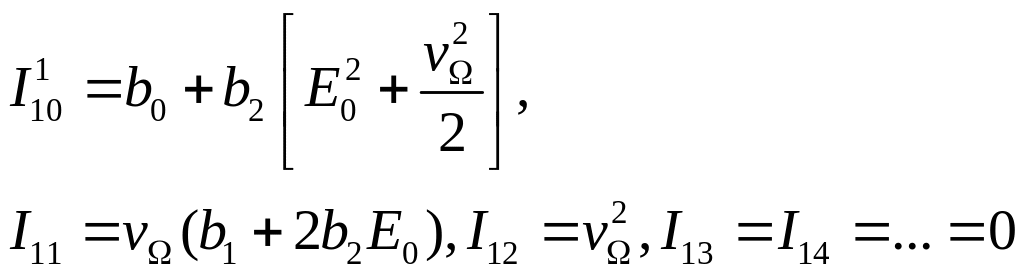
Подставляя в (18), получим:
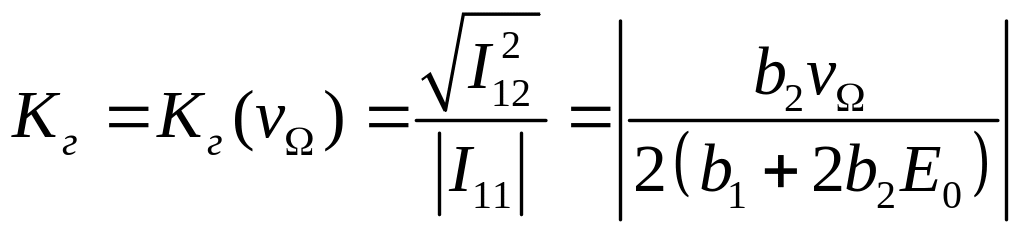 (21)
(21)
Подставляя
в (19) значения
при
![]() ,
найдем:
,
найдем:
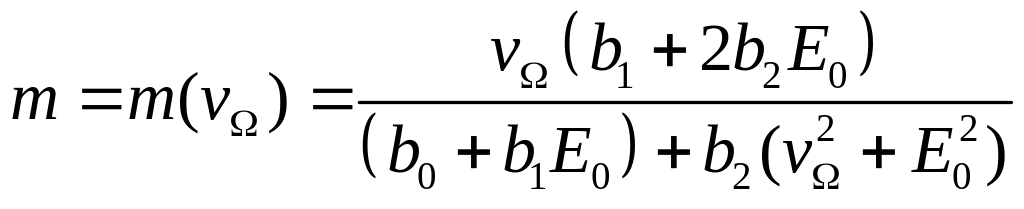 (22)
(22)
Пример 4.
Пусть модуляционная характеристика описывается выражением (17). В этом случае при расчёте Кг следует воспользоваться методом 5-ти ординат.
Обозначим
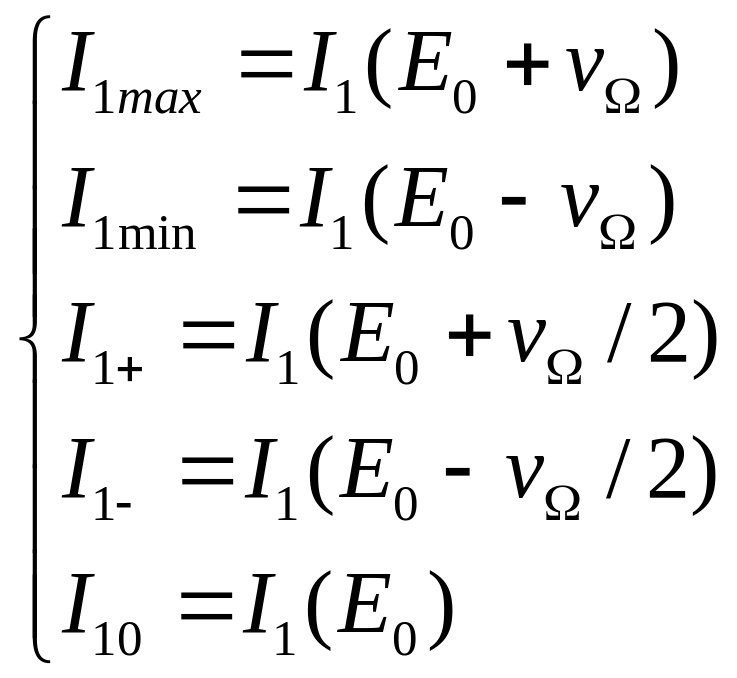 (23)
(23)
- точки
модуляционной характеристики,
соответствующие максимальному,
минимальному, промежуточному (половинному)
и нулевому значениям напряжения
модуляции.
![]() Тогда
Тогда
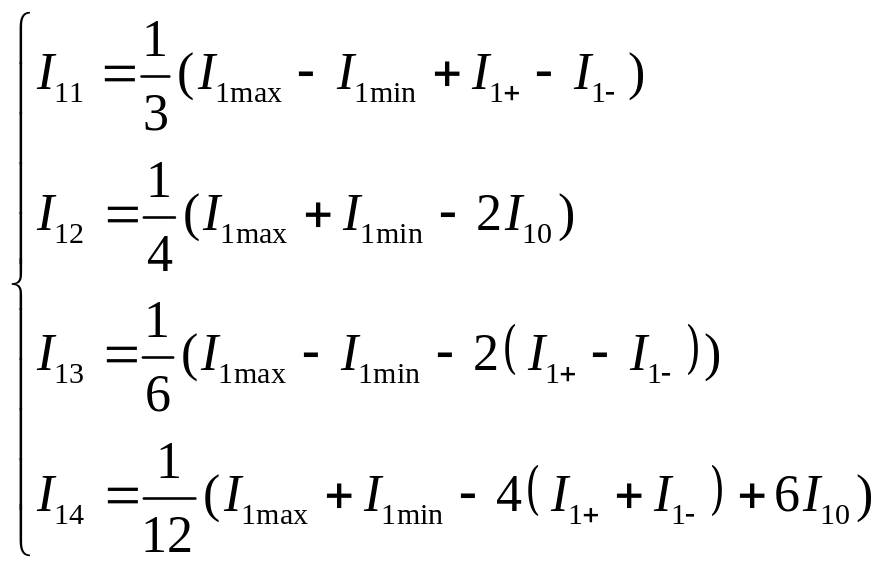 (24)
(24)
Выражения (24) есть формулы метода 5-ти ординат, записанные для приближённого определения амплитуд гармоник огибающей.
Порядок расчёта Кг в данном случае таков.
Задавшись
,
вычисляем по (23) и (17) соответствующие
значения
.
Эти значения используем для вычислений
по (24) амплитуд
![]() ,
полученные
величины подставляем в (18) и находим
Кг
при данном
.
Глубину модуляции по-прежнему определяем
по (19). Описанная процедура проделывается
для каждого выбранного значения
.
,
полученные
величины подставляем в (18) и находим
Кг
при данном
.
Глубину модуляции по-прежнему определяем
по (19). Описанная процедура проделывается
для каждого выбранного значения
.
Трудоёмкость расчётов существенно уменьшается, а точность растёт, если их вести на ЭВМ.
