Робота 3. Дослідження перехідних характеристик типових ланок

3.1. Мета роботи

Експериментально дослідити перехідні характеристики типових ланок систем автоматичного керування та навчитися визначати параметри ланок за їх перехідними характеристиками.

3.2. Теоретичні відомості

Для аналізу роботи систем автоматичного керування технологічними процесами чи технічними об’єктами необхідно знати математичні моделі об’єкта керування, керуючого пристрою та інших елементів системи, які прийнято називати ланками системи. Математичний опис (математична модель системи або ланки) у загальному випадку представляє собою систему диференціальних та алгебраїчних рівнянь, що встановлюють зв’язки між вхідними і вихідними величинами (сигналами).

Диференціальні рівняння характеризують поведінку системи у часі, коли в системі відбувається зміна кількості енергії або речовини і їх називають рівняннями динаміки. Для отримання рівнянь динаміки використовують різні аналітичні та експериментальні методи. Аналітичні методи грунтуються на законах фізики, хімії, електротехніки та інших.

У найпростішому випадку, при зосередженості параметрів ланок, стаціонарністі їх динамічних властивостей у часі та лінійності статичних характеристик відносно малих змін вхідних дій, динамічні властивості ланки описуються лінійним диференціальним рівнянням з постійними коефіцієнтами

/3.1/

де і - відповідно вхідна і вихідна величини, і - коефіцієнти.

Для опису властивостей ланок більш зручно користуватися не диференціальними рівняннями, а перерахованими нижче функціями і характеристиками, що безпосередньо випливають із диференціального рівняння:

– передаточною функцією ;

– перехідною характеристикою ;

– амплітудно-фазовою частотною характеристикою .

Для визначення передаточної і перехідної функцій ланки найбільш доцільно використовувати перетворення Лапласа, що грунтується на формулах прямого

/3.2/

і зворотного

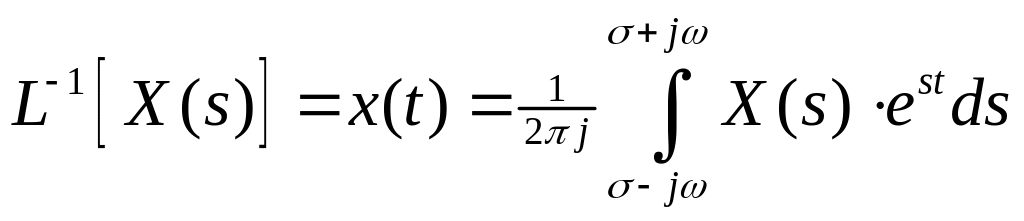. /3.3/

перетворень.

Тут під позначено комплексну змінну . При перетворення Лапласа переходить в його окремий випадок – в перетворення Фур’є.

Передаточною функцією лінійної ланки називають відношення зображення Лапласа вихідної величини до зображення вхідної величини при нульових початкових умовах:

. /3.4/

В операторній формі диференціальне рівняння /3.1/ приймає вигляд

/3.5/

Знайшовши із /3.5/ відношення зображень вихідної і вхідної величин, отримуємо вираз для передаточної функції

. /3.6/

З виразу передаточної функції видно, що вона є відношенням двох поліномів зі змінною і коефіцієнтами, рівними коефіцієнтам диференціального рівняння. Таким чином встановлюється однозначний зв’язок між передаточною функцією та диференціальним рівнянням.

Перехідною характеристикою ланки (системи) називають її реакцію на одиничну ступінчасту дію. Вона показує, як змінюється вихідна величина ланки, коли вхідна величина є одиничною ступінчастою функцією.

Математично одинична ступінчаста функція задається рівняннями

. /3.7/

Зображення Лапласа одиничної ступінчастої функції

. /3.8/

Тому для зображення перехідної характеристики отримуємо вираз

. /3.9/

Перейшовши від зображення до оригіналу, знаходимо вираз для перехідної характеристики

. /3.10/

Вираз /3.10/ встановлює зв’язок між перехідною характеристикою і передаточною функцією ланки. Тому за перехідною характеристикою системи можна оцінити її динамічні властивості. У випадку, коли перехідну характеристику визначено експериментальним шляхом, на її основі можуть бути встановлені параметри ланки.

Разом з тим, знаючи реакцію лінійної системи на ступінчасту дію, можна розрахувати реакцію на довільну дію, використавши інтеграл згортки:

. /3.11/

В роботі досліджуються перехідні характеристики типових ланок:

пропорційної - ;

інтегруючої - ;

диференціюючої - ;

аперіодичної - ;

коливної - .

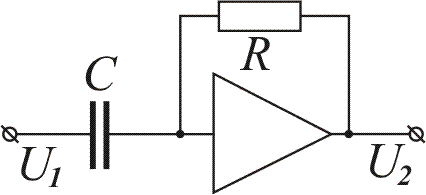
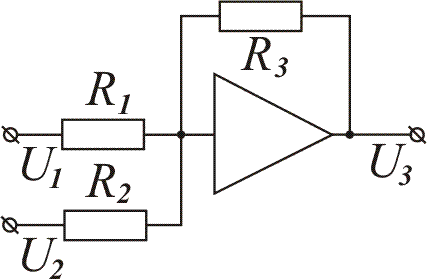
Лабораторна робота виконується із використанням моделюючого комплексу і системи керуючої лабораторної СУЛ-3. Динамічні властивості ланок системи моделюються електронними схемами на основі операційних підсилювачів. Електричні принципові схеми ланок та їх реалізація наведені в табл.3.1.

Таблиця 3.1

Типова ланка	Передаточна функція W(s)	Аналогова модель	Параметри ланки
Пропорційна
Інтегруюча

Продовження табл. 3.1

Типова ланка	Передаточна функція W(s)	Аналогова модель	Параметри ланки
Диференціююча
Аперіодична
Суматор