1.6. Симплексный метод решения задач линейного программирования

Рассмотрим следующую задачу линейного программирования

1. Прежде чем решать задачу симплексным методом, надо проверить, что правые части системы ограничений неотрицательны, т.е. . Если это не так, то в соответствующем ограничении меняем знак.

2. Далее исходную задачу надо записать в канонической форме, если она не имеет такой формы записи. Для этого каждое ограничение  неравенство вида надо превратить в равенство добавлением дополнительной неотрицательной (балансовой) переменной, а каждое ограничение  неравенство вида превратить в равенство вычитанием балансовой переменной. Таким образом, все ограничения в задаче будут уравнения с неотрицательными правыми частями.

3. Далее систему уравнений при помощи симплексных преобразований надо привести к единичному базису, т.е. найти исходное опорное решение .

4. Для того, чтобы проверить будет ли это решение оптимальным, надо составить оценочную строку (  строку) по следующему правилу: , где

 искомый элемент Z  строки;

 столбец коэффициентов целевой функции при базисных переменных;

 столбец коэффициентов при неизвестном ;

 столбец свободных членов;

 скалярное произведение указанных столбцов – векторов;

 коэффициент целевой функции при неизвестном

5. Для задачи на максимум.

Если в Z  строке все элементы положительные , то найдено оптимальное решение . Если же в Z  строке есть хоть один отрицательный элемент, то найденное решение не оптимально. Есть возможность его улучшения. Для этого среди отрицательных элементов Z  строки находим минимальный (например, ). Столбец с номером p становится разрешающим. Разрешающую строку выбираем по симплексным преобразованиям (для этого в симплексной таблице заводится последний столбец). В столбце с номером p в качестве разрешающего элемента берется положительный элемент, если он один. Если в этом столбце положительных элементов несколько, то берется тот из них, для которого отношение свободных членов к этим положительным элементам будет наименьшее. Если в столбце с номером p вообще нет положительных элементов, то задача не имеет оптимального решения и . После того, как разрешающий элемент найден, производим расчеты по методу Гаусса, включая и элементы Z  строки. Получаем новое опорное решение. После этого возвращаемся к началу пункта 5.

6. Для задачи на минимум. Если в Z  строке все элементы , то найдено оптимальное решение . Если же в Z  строке есть хоть один положительный элемент, то найденное решение не оптимально. Для улучшения решения среди положительных элементов  строки находим максимальный (например, ). Столбец с номером q становится разрешающим. Разрешающую строку ищем по симплексным преобразованиям (смотреть задачу на максимум.) Если в столбце с номером q нет положительных элементов, то задача не имеет оптимального решения и . После того, как разрешающий элемент выбран, выполняем расчеты по методу Гаусса, включая и элементы  строки, и получаем новое опорное решение. Переходим к началу пункта 6. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение или мы не убедимся, что его нет.

Пример 7. Решить задачу линейного программирования симплексным методом

Решение:

Приведем задачу к каноническому виду. Для этого в левую часть каждого неравенства типа добавляем новые дополнительные переменные , , (новые балансовые переменные). Таким образом, задача примет вид

Составляем симплекс таблицу.

	базис		7	-5	10	0	0	0
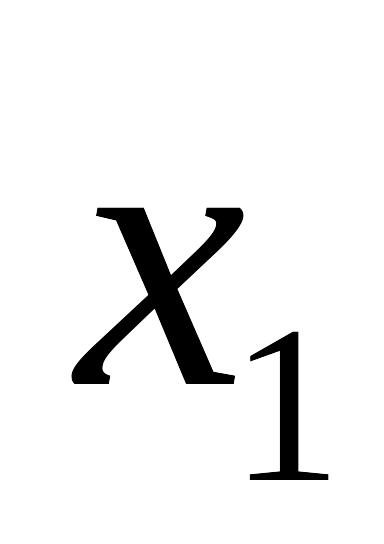
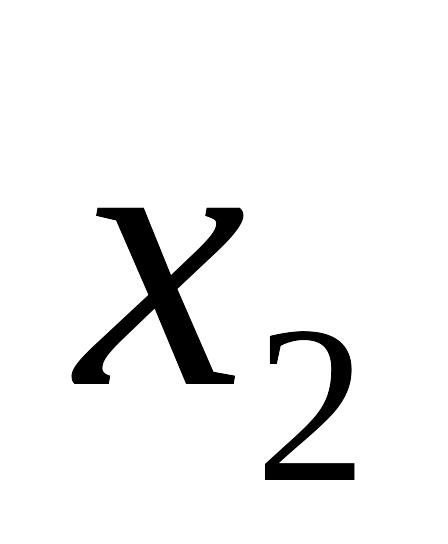
0		12	2	-2	3	1	0	0	–
0		2	-1	1	-1	0	1	0	2:1=2 – min
0		24	2	1	2	0	0	1	24:1=24
		0	-7	5	-10	0	0	0
		16	0	0	1	1	2	0
		2	-1	1	-1	0	1	0
		22	3	0	3	0	-1	1
		-10	-2	0	-5	0	-5	0

Так как есть исходное опорное решение, то составляем оценочную строку по следующему правилу: .

Так как среди есть одно положительное число, то столбик, в котором содержится этот элемент, выбираем в качестве разрешающего. Разрешающий элемент выбираем по методу минимального элемента ( ).

Далее вычисления производим по методу Жордана-Гаусса.

Так как все , то найденное решение оптимально, при этом , . Исходная задача имела три переменных, поэтому в ответе в оптимальном решении последние три дополнительные переменные не записываем.

Ответ: , .

Пример 8. Решить задачу линейного программирования симплексным методом

Решение:

Приведем задачу к каноническому виду:

Составляем симплекс таблицу.

	базис		3	-1	-4	0	0
		1	0	- 1	1	1	0	–
		2	-5	1	1	0	0	2:1=2 – min
		3	-8	1	2	0	-1	3:1=3
		3	-5	0	2	1	0	3:2=1,5
		2	-5	1	1	0	0	2:1=2
		1	- 3	0	1	0	-1	1:1=1– min
0		1	1	0	0	1	2	1:1=1
-1		1	-2	1	0	0	1	–
-4		1	-3	0	1	0	-1	–
		-5	1 1	0	0	0	3
		1	1	0	0	1	2
		3	0	1	0	2	5
		4	0	0	1	4	5
		-16	0	0	0	-11	-19

Ответ: , .