1.5. Графический метод решения задач линейного программирования

Рассмотрим систему

( неравенства в системе ограничений могут содержать знаки или )

Так как задача задана в стандартной форме (все ограничения- неравенства), то решение задачи происходит по следующим этапам:

1. Строят прямые, уравнения которых получаются в результате замены в ограничениях задачи знаков неравенств на знаки равенств, т. е.

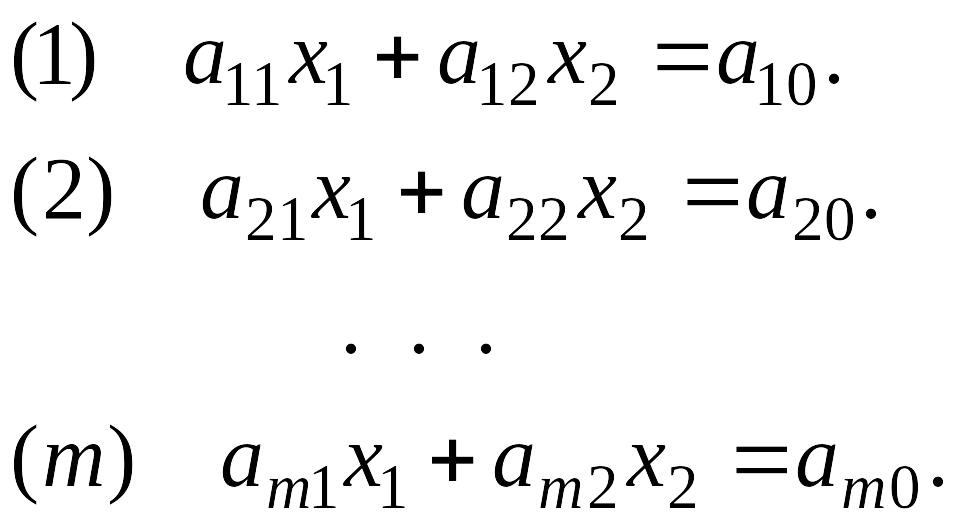
2. Находят полуплоскости, определяемые каждым из ограничений задачи. Для этого, например, в первое неравенство подставляют координаты любой точки, не лежащей на прямой (1). Если координаты этой точки удовлетворяют первому неравенству, то заштриховывают ту полуплоскость, где находится точка, а если нет, то противоположную относительно прямой (1) полуплоскость.

3. Пересечение всех полуплоскостей дает область возможных решений (ОВР).

4. Из этой области выделяем область допустимых решений (ОДР), т.е. пересечение области допустимых решений и первой четверти, где и . Таким образом, находим ОДР. Если ОДР пуста, то задача линейного программирования решений не имеет.

5. Строим вектор-градиент целевой функции , равный .

6. Строим линию уровня , перпендикулярно вектору градиенту ( - константа). Линий уровня бесконечно много и они все параллельны между собой.

7. Передвигая линию уровня в направлении вектора , находим точку «входа» в ОДР – это точка минимума, и точку «выхода» из ОДР – это точка максимума.

8. Определяем координаты точки минимума или максимума (в зависимости от условия задачи) аналитически и вычисляем значение целевой функции в этой точке.

Замечание.

1.		ОВР – открытый многоугольник , ОДР – открытый многоугольник , достигается в точке , .
2.		ОВР – треугольник , ОДР – многоугольник , достигается в точке , во всех точках отрезка , т.е. оптимальных решений бесконечное множество, причем , .
3.		ОВР и ОДР являются пустыми множествами, задача не имеет решения в виду несовместности системы ограничений.

Пример 6. Решить задачу линейного программирования графическим методом.

Решение:

Построим область допустимых решений. Каждое неравенство в системе ограничений заменяем на равенство. В прямоугольной декартовой системе координат строим прямые

Для того чтобы построить прямую достаточно знать координаты двух точек этой прямой. Прямые зададим таблично.

0 -2 2 0	0 2 -3 0
0 1 2 0	- прямая параллельна оси

Построив прямые, находим полуплоскости, определяемые данными неравенствами.

Т.к. первая прямая не проходит через начало координат, то подставим координаты точки О(0;0) в первое неравенство, получим , (верно), следовательно, первое неравенство определяет полуплоскость, лежащую ниже прямой (1).

Т.к. вторая прямая не проходит через начало координат, то подставим координаты точки О(0;0) во второе неравенство, получим , (верно), следовательно, второе неравенство определяет полуплоскость, лежащую выше прямой (2).

Т.к. третья прямая не проходит через начало координат, то подставим координаты точки О(0;0) в третье неравенство, получим , (не верно), следовательно, третье неравенство определяет полуплоскость, лежащую выше прямой (3).

Четвертое неравенство определяет полуплоскость, лежащую ниже прямой (4).

Находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности. Заштрихованный многоугольник является областью допустимых решений (ОДР).

Строим вектор градиент .

Строим линию уровня перпендикулярно вектору .

По условию задачи нужно найти максимум и минимум функции Z. Передвигая линию уровня параллельно самой себе в направлении возрастания вектора градиента, находим точку «входа» в ОДР- это точка . Найденная точка является точкой минимума. Найдем координаты точки аналитически. Эта точка является пересечением прямых (3) и . Решим систему:

Следовательно, . Вычислим значение целевой функции в этой точке. .

Аналогично, находим точку «выхода» из ОДР- это точка . Найденная точка является точкой максимума.

Найдем координаты точки аналитически. Эта точка является пересечением прямых (2) и (4). Решим систему:

Следовательно, . Вычислим значение целевой функции в этой точке. .

Ответ: , .