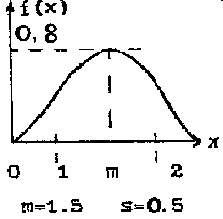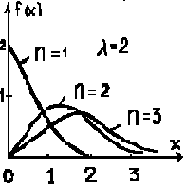Int ns, /*наличие заявки на входе системы*/

sm1, /*состояние ЭВМ1

( ЭВМ1 = 0, если ЭВМ1 свободна;

ЭВМ1 = 1, если ЭВМ2 занята)*/

sm2, /*состояние ЭВМ2*/

kr1, /*количество заявок, выполненных на ЭВМ1*/

kr2, /*количество заявок, выполненных на ЭВМ2*/

kot, /*количество отказов в обслуживании пользователей*/

t, /*текущее время работы системы*/

tektm1, /*текущее время обработки задания на ЭВМ1*/

tektm2, /*текущее время обработки задания на ЭВМ2*/

tektps; /*текущее время между поступлениями заявок*/

float

proz ; /*процент заявок, выполненных на ЭВМ1*/

FILE *f1,*f2; /*файловые переменные*/

main()

{

/*подготовка работы с файлами exp.dat и norm.dat*/

f1=fopen(“norm.dat”,”rb”);

f2=fopen(“exp.dat”,”rb”);

randomize(); /*инициализация ГРРПСЧ*/

/*установка начальных условий*/

ns=1; sm1=0; sm2=0;

kr1=0; kr2=0; kot=0;

tektm1=0; tektm2=0; tektps=0;

/* чтение из файла norm.dat ПСЧ – времени обработки задания на ЭВМ1*/

fread(&tm1,sizeof(tm1),1,f1);

/* чтение из файла exp.dat ПСЧ – времени обработки задания на ЭВМ2*/

fread(&tm2,sizeof(tm2),1,f2);

tps=(float)random(1000)/1000; /*определение времени между поступлением заявок

как РРПСЧ в интервале (0,1)*/

tps=1+4*tps; /*приведение к заданному интервалу*/

for (t=0; t<=480; t++) /*условие продолжения работы системы*/

{ /*изменение текущего времени между заявками*/

if (++tektps>=tps) /*поступила очередная заявка*/

{

ns=1;

tektps=0;

/*определение времени между поступлением заявок как РРПСЧ в

интервале (0,1)*/

tps=(float)random(1000)/1000;

/*приведение к заданному интервалу*/

tps=1+4*tps;

}

if (sm1) /*ЭВМ1 обрабатывает заявку*/

/*изменение текущего времени работы ЭВМ1*/

if (++tektm1>tm1) /*заявка выполнена*/

{

sm1=0; /*освобождаем ЭВМ1*/

tektm1=0;

kr1++;

/*чтение из файла norm.dat ПСЧ – времени обработки задания

на ЭВМ1*/

fread(&tm1,sizeof(tm1),1,f1);

}

if (sm2) /*ЭВМ2 обрабатывает заявку*/

/*изменение текущего времени работы ЭВМ2*/

if (++tektm2>tm2) /*заявка выполнена*/

{

sm2=0; /*освобождаем ЭВМ2*/

tektm2=0;

kr2++;

/*чтение из файла exp.dat ПСЧ – времени обработки задания

на ЭВМ2*/

fread(&tm2,sizeof(tm2),1,f2);

}

if (ns) /*на входе имеется заявка*/

{

if (!sm1)

{

sm1=1; /*занимаем ЭВМ1*/

tektm1++;

}

else /*ЭВМ1 занята*/

if (!sm2)

{ /*ЭВМ2 свободна*/

sm2=1; /*занимаем ЭВМ2*/

tektm2++;

}

else kot++; /*обе машины заняты*/

/*отказ в обслуживании*/

ns=0;

}

} /*переход к следующему моменту модельного времени*/

/*система отработала заданное время*/

proz=kr1*100/(kr1+kr2+kot);

fclose(f1); /*закрытие файлов*/

fclose(f2);

/*вывод результатов на экран*/

clrscr();

printf("\n\n\r за 8 часов работы системы на ЭВМ1 выполнено %f",proz,

"%% поступивших заявок");

printf("\n\r на ЭВМ2 выполнено %f",(float)kr2*100/(kr1+kr2+kot),

"%% поступивших заявок");

printf("\n\r отказано в обслуживании %f",(float)kot*100/(kr1+kr2+kot),

"%% \n\r");

puts("\n\n\rнажмите на <ВВОД>");

getch();

}

Вывод. Значение выходных характеристик, полученные при прогонах модели с различными случайными воздействиями, будут отличны друг от друга. Усредненное по многим прогонам модели значение выходной характеристики незначительно отличается от соответствующей детерминированной величины, что подтверждает правильность работы модели.

Порядок выполнения работы

1. Изучить теоретический материал по данной теме.

2. Преобразовать детерминированную модель вычислительной системы (результат лабораторной работы №1) в стохастическую модель.

3. Оценить результаты работы модели, полученные при ее прогонах с различными случайными воздействиями.

4. Оформить и защитить отчет по лабораторной работе.

Лабораторная работа №8

ПОСТРОЕНИЕ СТОХАСТИЧЕСКОЙ МОДЕЛИ ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ НА ЯЗЫКЕ МОДЕЛИРОВАНИЯ GPSS

Цель работы: изучение возможностей языка моделирования GPSS. Построение имитационной модели изучаемой вычислительной системы на языке моделирования GPSS, ее сравнение с ранее созданной моделью на универсальном языке программирования.

Пример. Создать на языке моделирования GPSS стохастическую модель вычислительной системы, заданной концептуально (в лабораторной работе №1).

Получить сравнительные оценки моделей, созданных на универсальном языке программирования и на языке моделирования GPSS.

GPSS-модель имеет вид:

SIMULATE

* задание функции для генерации ПСЧ, имеющего экспоненциальный закон

* распределения с m=1

EXPON FUNCTION RN1, C24

0.0/.1,.104/.2,.222/.3,.35/.4,.509/.5,.69/.6,.915/.7,1.2/.75,1.38

0.8,1.6/.84,1.83/.88,2.12/.9,2.3/.92,2.52/.94,2.81/.95,2.81

.096,3.2/.97,3.5/.98,3.9/.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

* задание функции для генерации ПСЧ, имеющего нормальный закон

* распределения с m=0, D=1

NORM FUNCTION RN2, C25

0,-5/.0003,-4/.00135,-3/.00621,-2.5/.02275,-2/.06681,-1.5

.11507,-1.2/.15866,-1/.21186,-.8/.27425,-.6/.34458,-4

.42074,-.2/.5,0/.57926,.2/.65542,.4/.72575,.6/.78814,.8

.84134,1/.88493,1.2/.93319,1.5/.97725,2/.99379,2.5/.99865,3

.99997,4/1,5

* приведение нормально распределенного ПСЧ к заданному интервалу

* (m=6, D=2)

TIBM1 FVARIABLE 6+1.414*FN$NORM

SUM FVARIABLE FC$IBM1+FC+IBM2+X$KOT

* FC – (СЧА) счетчик числа занятий прибора

* Х – значение ячейки памяти

GENERATE 3,2 приход пользователей

TEST E F$IBM1,0,ZANM2

* F – (СЧА) состояние прибора

SEIZE IBM1 занятие ЭВМ1, если она свободна

ADVANCE V$TIBM1 обработка задания за данное время

V – (СЧА) значение арифметической переменной

RELEASE IBM1 освобождение ЭВМ1

TRANSFER , KON переход на метку

ZANM2 TEST E F$IBM2,0, UDAL

SEIZE IBM2 занятие ЭВМ2, если она свободна

ADVANCE 7,FN$EXPON обработка задания за данное время

RELEASE IBM2 освобождение ЭВМ2

TRANSFER , KON

UDAL SAVEVALUE KOT+,1 отказ в обслуживании

KON TERMINATE удаление заявки из системы

сегмент программы, управляющий временем работы модели

GENERATE , ,480

SAVEVALUE PROZ, FC$IBM1*100/V$SUM

TERMINATE 1

START 1

END

Полученные оценки сведены в табл. 2.

Модель	Время создания модели	Объем исходного модуля
Модель на универсальном языке программирования	2 часа	PAS – 4 Кб С – 3,5 Кб
GPSS – модель	10 мин	1,5 Кб

Вывод. Использование языка GPSS значительно упрощает процесс моделирования различных систем благодаря ряду преимуществ по сравнению с универсальными языками программирования.

Порядок выполнения работы

1. Изучить теоретический материал по данной теме /6/.

2. Создать на языке моделирования GPSS стохастическую модель вычислительной системы, заданной концептуально в лабораторной работе №1.

3. Сравнить GPSS-модель с ранее созданной моделью на универсальном языке программирования.

4. Оформить и защитить отчет по лабораторной работе.

Приложение 1

Сведения о непрерывных случайных величинах /4,5/

NN п/п	Закон распре-деления случайной величины	Аналитическое выражения плотности вероятности	График y=f(x)	Область значе-ний случай-ной велич-ины	Определяющие параметры	Числовые характеристики		Алгоритм получения случайной величины
						Математичес кое ожидание m	Дисперсия D
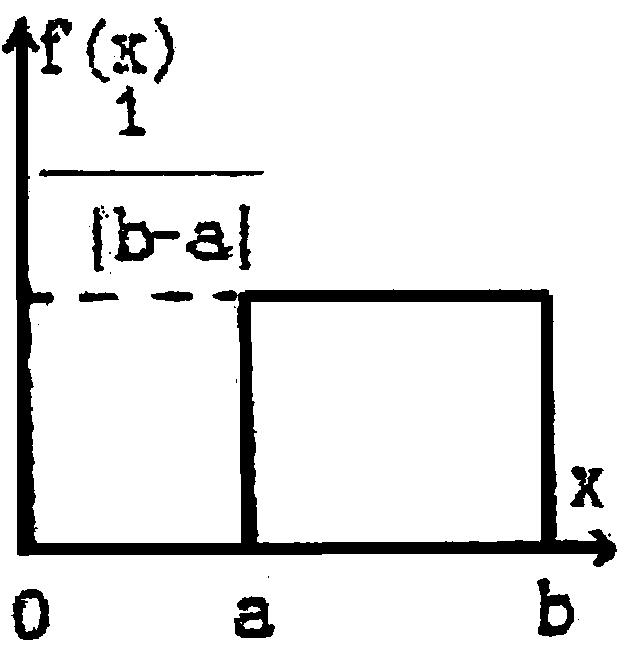
1.	Равно- мерный R(a,b)			[a,b] b>a	a,b |a|< |b|<			xi=a+(b-a)zi
2.	Нормаль- ный (Гаусса) N(m,σ)				|m|<	m	σ2	Для m=0,D=1(N(0,1)) a) k=12, k=24; b)
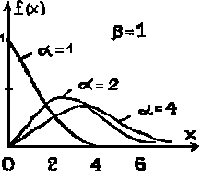
3.	Гамма- распре-деление G(α,b)	- гамма-функция		[0, )	α,β α>0 β>0	αβ	αβ2	а) б) в)
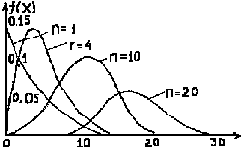
4.	Эрланга n-го порядка G(n,1/λ)			[0, )	λ>0 n= 1,2,…	n/λ	n/λ2	а) б) в)
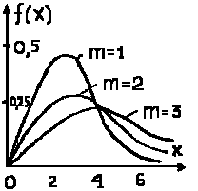
5.	Показа-тельно-степенной G(m+1,1)			[0, )	m= 1,2,3...	m+1	m+1	а) б) в)
6.	Хи-квадрат G(n/2,2)= χ2(n)			[0, )	n=1,2,…	n	2n	а) б)
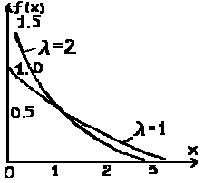
7.	Экспонен-циальный G(1,1/λ)= Э(λ)			[0, )	λ>0	1/λ	1/λ2
8.	Рэлея Re(0,σ)			[0, )	σ>0			а) б) в)
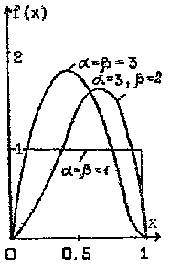
9.	Бета-распреде-ление Be(α,β)			(0,1)	α,β α>0 β>0
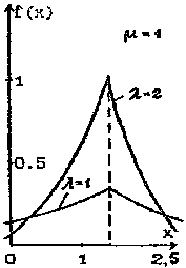
10.	Лапласа L(μ,λ)			(- , + )	λ>0 |μ|<	μ	2/λ2

Примечание.

z_i – имеет равномерное распределение в интервале (0,1)

l_i – имеет экспоненциальное распределение с параметром λ=1

у_i – имеет нормальное распределение с параметрами m=0, D=1

Приложение 2