1. Определение числовых характеристик (табл.1).

№ п/п	Характеристика	Теоретическое значение	Статистическое значение
1	Наименьшее значение среди совокупности	m-3σ=1.77	1.889115
2	Наибольшее значение среди совокупности	m+3σ=10.23	10.365674
3	Начальный момент 1-го порядка (математическое ожидание)	m=6	6.281302
4	Центральный момент 2-го порядка (дисперсия)	D=2	1.990851
5	Среднее квадратическое отклонение		1.410975
6	Коэффициент асимметрии	0	-0.007720
7	Эксцесс	0	-0.008965

2. Аппроксимация статистического распределения теоретической функцией.

Плотность распределения для нормального закона имеет вид:

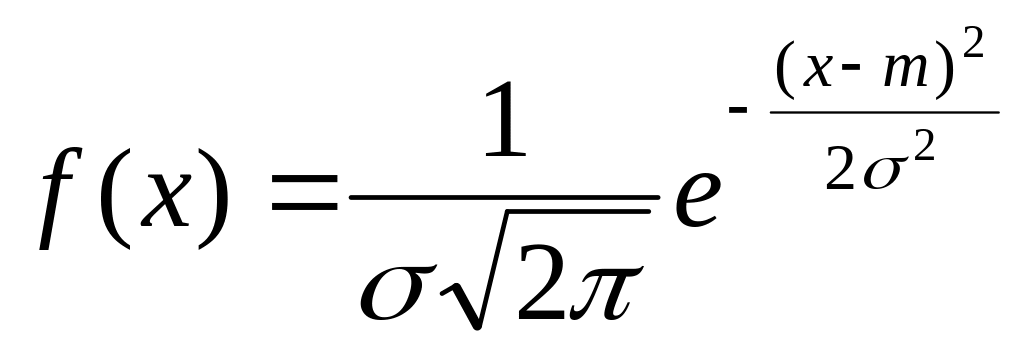
Область значений случайной величины . С помощью системы ANALIZE.EXE получают совмещенные графики статистической (гистограмма) и теоретической функций распределения.

3. Проверка соответствия чисел последовательности требуемому распределению дает следующие результаты:

Критерий хи-квадрат: значение χ²=2.316844.

С доверительной вероятностью 0.72 можно говорить о согласованности теоретических и статистических данных.

Критерий Колмагорова.

Максимальная разность max|F(x)-F*(x)|=0.017.

С доверительной вероятностью 0.93 можно говорить о согласованности теоретических и статистических данных.

4. Определение характеристик корреляции.

График зависимости коэффициента корреляции от корреляционного расстояния τ приведен на рис. 11.

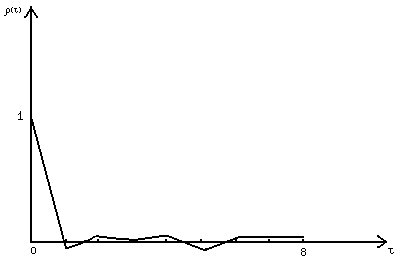
Рис. 11. График изменения коэффициента корреляции

Вывод. Полученная по алгоритму, описанному в лабораторной работе №5, последовательность ПСЧ, имеющая нормальный закон распределения, удовлетворяет предъявляемым требованиям к качеству и может быть использована в задачах моделирования, так как:

- числовые характеристики имеют незначительное отклонение от теоретических значений;

- по критериям согласия получены удовлетворительные значения доверительных вероятностей;

- числа последовательности достаточно независимы, о чем свидетельствует график ρ(τ).

Порядок выполнения работы

1. Оценить качество полученных в лабораторной работе №5 последовательностей ПСЧ, пользуясь автоматизированной системой ANALYZE.EXE.

2. Проанализировав результаты исследований, сделать вывод о качестве каждой последовательности и о возможности их использования в задачах моделирования.

3. Оформить и защитить отчет по лабораторной работе.

Лабораторная работа №7

ПОСТРОЕНИЕ СТОХАСТИЧЕСКОЙ МОДЕЛИ ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ

Цель работы: переход от детерминированной модели к стохастической, получение и анализ результатов выполнения стохастической модели.

Стохастическая имитационная модель создается дополнением детерминированной модели необходимыми обращениями к генераторам или файлам случайных чисел в тех позициях, где требуется моделирование стохастических потоков.

Пример. Преобразовать детерминированную модель вычислительной системы (результат лабораторной работы №1) в стохастическую модель. При решении задачи будем использовать:

- программный генератор РРПСЧ – встроенную функцию random(), возвращающую РРПСЧ в интервале (0,1);

- файл NORM.DAT ПСЧ, имеющий нормальный закон распределения с m=6, D=2, созданный в лабораторной работе №5;

- файл EXP.DAT ПСЧ, имеющий экспоненциальный закон распределения с m=7, созданный в лабораторной работе №5.

Соответствующие изменения внесем в детерминированную программу.

Стохастическая моделирующая программа на языке Паскаль.

program model(input,output);

uses crt;

var

tps, {время между приходом заявок}

tm1, {время обработки задания на ЭВМ1}

tm2: real; {время обработки задания на ЭВМ2}

ns, {наличие заявки на входе системы}

sm1, {состояние ЭВМ1

( ЭВМ1 = false, если Эвм1 свободна;

ЭВМ1 = true, если ЭВМ1 занята)}

sm2: boolean; {состояние ЭВМ2}

kr1, {количество заявок, выполненных на ЭВМ1}

kr2, {количество заявок, выполненных на ЭВМ2}

kot: integer; {количество отказов в обслуживании пользователей}

t, {текущее время работы системы}

tektm1, {текущее время обработки задания на ЭВМ1}

tektm2, {текущее время обработки задания на ЭВМ2}

tektps: integer; {текущее время между поступлениями заявок}

proz: real; {процент заявок, выполненных на ЭВМ1}

f1,f2: file of real; {файловые переменные}

begin

{подготовка работы с файлами norm.dat и exp.dat}

assign(f1,’norm.dat’); assign(f2,’exp.dat’);

reset(f1); reset(f2);

randomize; {инициализация ГРРПСЧ}

{установка начальных условий}

ns:= true; sm1:= false; sm2:= false;

kr1:=0; kr2:=0; kot:=0;

tektm1:=0; tektm2:=0; tektps:=0;

t:=0;

{чтение из файла norm.dat ПСЧ – времени обработки задания на ЭВМ1}

read (f1, tm1);

{чтение из файла exe.dat ПСЧ – времени обработки задания на ЭВМ2}

read (f2, tm2);

tps:=random; {определение времени между поступлением заявок как РРПСЧ в

интервале (0,1)}

tps:=1+4*tps; {приведение к заданному интервалу}

while t <= 480 do {условие продолжения работы системы}

begin

tektps:=tektps+1; {изменение текущего времени между заявками}

if tektps>=tps then {поступила очередная заявка}

begin

ns:=true;

tektps:=0;

{определение времени между поступлением заявок как

РРПСЧ в интервале (0,1)}

tps:=random;

{приведение к заданному интервалу}

tps:=1+4*tps;

end;

if sm1 then {ЭВМ1 обрабатывает заявку}

begin

{изменение текущего времени работы ЭВМ1}

tektm1:=tektm1+1;

if tektm1>tm1 then {заявка выполнена}

begin

sm1:=false; {освобождаем ЭВМ1}

tektm1:=0;

kr1:=kr1+1;

{чтение из файла norm.dat ПСЧ – времени

обработки задания на ЭВМ1}

read(f1,tm1);

end;

end;

if sm2 then {ЭВМ2 обрабатывает заявку}

begin

{изменение текущего времени работы ЭВМ2}

tektm2:=tektm2+1;

if tektm2>tm2 then {заявка выполнена}

begin

sm2:=false; {освобождаем ЭВМ2}

tektm2:=0;

kr2:=kr2+1;

{чтение из файла exp.dat ПСЧ – времени

обработки задания на ЭВМ2}

read(f2,tm2);

end;

end;

if ns then {на входе имеется заявка}

begin

if not sm1

then {ЭВМ1 свободна}

begin

sm1:= true; {занимаем Эвм1}

tektm1:=tektm1+1;

end

else {ЭВМ1 занята}

if not sm2

then {ЭВМ2 свободна}

begin

sm2:= true; {занимаем ЭВМ2}

tektm2:=tektm2+1;

end

else {обе машины заняты}

kot:=kot+1; {отказ в обслуживании}

ns:=false;

end;

{переход к следующему моменту модельного времени}

t:=t+1;

end;

close(f1); close(f2); {закрытие файлов}

{система отработала заданное время}

proz:=kr1*100/(kr1+kr2+kot);

{вывод результатов на экран}

clrscr; writeln; writeln;

writeln('за 8 часов работы системы на ЭВМ1 выполнено',

proz:7:1,'% поступивших заявок:');

writeln('на ЭВМ2 выполнено',(kr2*100/(kr1+kr2+kot)):7:1,

'% поступивших заявок:');

writeln('отказано в обслуживании',(kot*100/(kr1+kr2+kot)):7:1,'%');

writeln; writeln('нажмите на <ВВОД>');

readln;

end.

Стохастическая моделирующая программа на языке Си.

#include<stdio.h>

#include<conio.h>

float

tps, /*время между приходом заявок*/

tm1, /*время обработки задания на ЭВМ1*/

tm2; /*время обработки задания на ЭВМ2*/