Порядок выполнения работы

1. Изучить теоретический материал по данной теме.

2. Используя систему GENERATO.EXE. смоделировать работу генератора ПСЧ, основанного на регистре сдвига. В качестве исходных данных рекомендуется задать структуру ГПСЧ, отобранную по итогам лабораторного занятия №2.

Результат выполнения данного пункта – файл ПСЧ.

3. Используя программный ГПСЧ, созданный на лабораторном занятии №3, создать второй файл ПСЧ.

4. Применяя систему ANALYZE.EXE, проанализировать качество аппаратного и программного генераторов ПСЧ (по двум файлам чисел).

5. Проанализировав результаты исследований, сделать вывод о качестве созданных Вами аппаратного и программного ГПСЧ, отобрать лучший из них для дальнейшего применения в статистическом моделировании.

6. Удалить созданные Вами в процессе работы файлы данных.

7. Результаты исследований по двум файлам оформить в отчет по лабораторной работе.

Замечание. Формируемые в п.2,3 файлы должны содержать не менее 5000-10000 чисел. Файлы рекомендуется создавать на диске b: и сопровождать расширением _*.dat.

Лабораторная работа №5

ФОРМИРОВАНИЕ И ИСПОЛЬЗОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ С ТРЕБУЕМЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ.

Цель работы: изучение основных способов формирования последовательностей случайных чисел с заданным законом распределения и создание соответствующих файлов чисел.

При реализации статистического моделирования на ЭВМ возникает потребность не только в последовательностях случайных чисел, имеющих равномерный закон распределения, но и в последовательностях с иными законами распределения. Будем называть закон распределения «стандартным», если вид его функции распределения или функции плотности распределения и параметры распределения известны (нормальный, экспоненциальный, пуассоновский, рэлеевский, гамма-распределение, эрланговский, гиперэрланговский и т.д.). Для таких законов распределения, имея соответствующую процедуру формирования чисел по стандартному закону, необходимо в каждом конкретном случае привести случайные числа в соответствие заданным параметрам (математическому ожиданию и дисперсии; интенсивности для экспоненциального закона и т.д.).

Будем называть закон распределения «законом пользователя», если вид функции распределения известен только пользователю и задан либо в табличном виде (заданы значения абсцисс и соответствующие им значения ординат кривой распределения), либо в виде гистограммы, либо в аналитическом виде.

Как и для равномерно распределенных последовательностей, для получения последовательностей, распределенных по другим законам распределения, используются три основных способа: табличный, программный и аппаратный.

Суть табличного способа не отличается от изложенного в описании к лабораторной работе №2.

Программный способ

Основные методы программного способа следующие:

1. Метод, основанный на аналитическом преобразовании зависимости между заданной функцией распределения F(x) случайной величины X и случайной равномерно распределенной в интервале (0,1) переменной Z. Этот метод называется методом обратной функции.

2. Метод Неймана или метод исключения, основанный на отбраковывании точек, не принадлежащих области, ограниченной допустимыми значениями.

3. Метод ступенчатой аппроксимации.

1. Метод обратной функции

Метод основан на следующих свойствах функции распределения. По определению функции распределения F(x)=P(X<x), причем для х₁<x₂ F(x₁)<F(x₂); F( )=0; F(+ )=1. Для непрерывной функции распределения F(x) существует обратная ей функция F^-1(y), т.е., если y=F(x), то x=F^-1(y), , где f(x) – функция плотности распределения. Доказано, что случайная величина имеет равномерное в интервале (0,1) распределение. Поэтому для получения значения х необходимо решить относительно х уравнения:

X=F^-1(z).

Эта зависимость приводит к следующему алгоритму:

1. получить равномерно распределенное число z_i.

2. получить число х_i, имеющее функцию распределения F(x) по формуле x_i=F^-1(z_i) .

Пример. Пусть F(x) – экспоненциальная функция распределения с параметром , т.е. F(x)=1-e^λx. Тогда

.

Аналогично строятся и алгоритмы для дискретных распределений, для которых дифференциальное распределение вероятностей имеет вид:

xk	x1	x2	…	xj
p(X=xk)	p1	p2	…	pj

Тогда алгоритм вычисления значений случайных величин следующий:

1. получить равномерно распределенное число z_i;

2. получить число х_i по правилу:

если z_i<p₁, то х_i=х₁, иначе,

если z_i<p₁+p₂, то х_i=х₂, иначе,

если z_i<p₁+p₂+…+p_j, то х_i=х_j.

Основной недостаток метода обратных функций тот, что не всегда удается определить обратную функцию F^-1(y).

2. Метод Неймана

Пусть функция плотности распределения ограничена интервалом (А,В) (рис. 8).

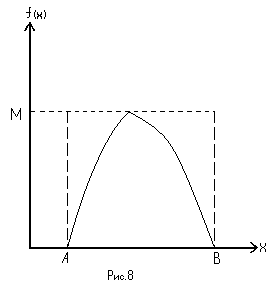
Обозначим через М максимальное значение функции f(x). Алгоритм получения случайной величины, основанный на методе Неймана, следующий:

1. получить два равномерно распределенных в интервале (0,1) числа z₁ и z₂;

2. вычислить х_i=А+(В-А)z₁;

3. проверить условие z₂ ≤ f(x)/M. Если условие выполняется, то х_i принимается в качестве реализации х_i, если нет, то отвергается.

Этот метод достаточно универсален, однако он обладает низким быстродействием из-за сложности вычисления f(x_i). Кроме того, выходные последовательности являются асинхронными.

3. Метод ступенчатой аппроксимации

Согласно этому методу функцию плотности распределения, заданную на отрезке (А,В), разбивают на N интервалов, полагая в пределах каждого интервала значения х равновероятными (рис. 9).

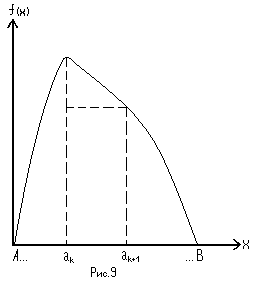
С учетом принятого допущения случайную величину х можно представить в виде: х=а_k+у_k, у_k – равномерно распределенная в интервале (а_k, а_k+1) величина.

Алгоритм, основанный на методе ступенчатой аппроксимации, следующий:

1. получить равномерно распределенное в интервале (0,1) число z₁;

2. с помощью этого числа выбрать интервал (а_k,а_k+1);

3. получить z₂;

4. получить x_i=( а_k+1- а_k)z₂+а_k.

Данный метод является приближенным.

Кроме описанных методов, обладающих достаточной универсальностью, для ряда стандартных законов существуют методы, основанные на свойствах конкретного закона; их алгоритмы приведены в приложениях 1, 2.

Пример. Создать процедуру формирования случайных чисел, распределенных по нормальному закону с параметрами m=6, D=2. Числа, имеющие данный закон, можно формировать на основе равномерных чисел по следующей формуле:

где z₁ и z₂ – равномерно распределенные в интервале (0,1) числа; х_i и х_i+1 – числа, имеющие нормальное распределение с m=0, D=1.

Для получения нормально распределенных чисел у_i с заданным математическим ожиданием с и дисперсией b следует осуществить следующее преобразование над числами х:

Процедура написана на языке Turbo Pascal и возвращает два требуемых числа за одно обращение.

PROCEDURE NORM (var x1, x2: real);

var

z1, z2: real;

begin

z1:= random;

z2:= random; {x1 и x2 с параметрами m=0, D=1}

x1:= sqrt(-2*ln(z))*cos(2*pi*z2);

x2:= sqrt(-2*ln(z))*sin(2*pi*z2);

{преобразование к нужным параметрам}

x1:= sqrt(2)*x1+6;

x2:= sqrt(2)*x2+6;

end;

Обращение к процедуре имеет вид: NORM(y1,y2);

Здесь у1 и у2 – искомые числа.