4.2.2. Способы устных вычислений

При обучении устным вычислительным действиям школьник осваивает в течение первого и второго года обучения в четырехлетней начальной школе целый ряд вычислительных приемов, из которых 12 относятся к вычислениям в пределах 100.

Вопрос о значимости формирования устных вычислительных навыков на сегодняшний день является весьма дискуссионным в методическом плане. Повсеместное использование калькуляторов ставит под сомнение необходимость «жесткой» отработки этих умений. На сегодняшний день никто не связывает хорошее владение арифметическими вычислениями с математическими способностями и математической одаренностью. Однако внимание к устным арифметическим вычислениям является традиционным для русской школы. В связи с этим на сегодня в программах по математики для начальных классов поставлена цель формирования устных вычислительных умений и навыков.

В жизни людям довольно часто приходится выполнять несложные (в пределах 100) вычисления в уме, а также довольно часто требуется умение оценить возможные границы результатов несложных вычислений. По этой причине учащихся необходимо учить приемам устных вычислений. Кроме того, психологи доказали, что формирование и развитие собственной вычислительной деятельности школьника положительно действует на развитие внутреннего плана действий, гибкость и рациональность мышления.

Часто школьники испытывают большие трудности при устных вычислениях в пределах 100. А.В. Белошистая считает, что учить младших школьников сразу приемам письменных вычислений – значит, с первых же шагов обрекать их на полную беспомощность при выполнении устных вычислений уже в пределах 100. По ее мнению научить приемам письменных вычислений иногда проще, чем пытаться развивать собственную вычислительную деятельность ученика. Особые трудности с устными вычислениями часто испытывают школьники с замедленным типом мышления, дети с ведущим синтетическим способом мыслительной деятельности, а также ведущие кинестетики (дети, которые предпочитают опору на пальцевый счет).

А.В. Белошистая предлагает перейти к схематической десятичной модели, что позволяет учащемуся моделировать сам прием вычисления.

Как замечает названный автор, эту десятичную модель числа школьники назвали

солнышком

Учащимся можно показать другие приемы вычисления. Прием вычисления складывается из ряда последовательных операций (системы операций), выполнение которых приводит к нахождению результата требуемого арифметического действия над числами.

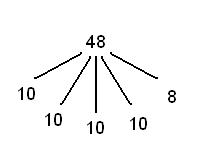
Прием может быть сформулирован в виде правила. Например: «Чтобы прибавить число 3, можно сначала прибавить 2, потом 1, или можно сначала прибавить 1, потом 2, или можно прибавить 1, потом 1, потом еще 1». В других случаях прием можно представить в виде рассуждения. «Пусть из48 нужно вычесть 25. Можно выполнить действия в таком порядке: 48 заменим суммой двух чисел 40 и 8, а число 25 – суммой чисел 20 и 5. Из 40 вычтем 20, будет 20. Из 8 вычтем 5, будет 3. 20 да 3будет 23. Ответ: 23».

В рассуждениях можно прибегать к ссылке на изученные свойства. Например: «2 + 5. Мы знаем, что от перестановки мест слагаемых сумма не меняется. Поменяем местами слагаемые, получим 5 + 2. К 5 легче прибавить 2. 5 и 2 - это 7, значит 2 + 5 - это тоже 7».

Выбор операций в каждом приеме определяется теми теоретическими положениями, которые используются в качестве его теоретической основы.

Например, при сложении чисел 57 и 25 в качестве теоретической основы может выступать:

1. Свойство прибавления суммы к числу: 57 + 25 = 57 + (20 + 5) = 77 + 5.

Прием включает три операции:

1. замена числа 25 суммой разрядных слагаемых 20 и 5;

1. прибавление к числу 57 слагаемого 20;

1. прибавление к результату (к 77) слагаемого 5.

2. Свойство прибавления суммы к сумме: 57 + 25 =^: (50 + 7) + (20 + 5) = (50+ 20)+ (7+ 5) = 70+ 12.

Прием для этого же случая включает 5 операций:

1. а) замена числа 57 суммой разрядных слагаемых 50 и 7;

2. б) замена числа 25 суммой разрядных слагаемых 20 и 5;

3. в) сложение чисел 50 и 20;

4. г) сложение чисел 7 и 5;

5. д) сложение полученных результатов 70 и 12.

Число операций зависит так же от чисел, над которыми выполняются арифметические действия. Так, прием сложения чисел 54 и 25 содержит меньше операций, чем прием сложения чисел 257 и 425, при использовании одной и той же теоретической основы - свойства прибавления суммы к сумме.

Число операций, выполняемых для нахождения результата арифметического действия, может сокращаться по мере овладения приемом, например, для случаев вида 8 + 2 на начальной стадии формирования умения вычислять подобные случаи ученик выполняет три операции:

а) замена числа 2 суммой чисел 1 и 1 (хотя в явном виде эта операция не дается);

б) прибавление числа 1 к 8;

в) прибавление числа 1 к результату (к 9).

Однако после заучивания таблицы сложения этот прием теряет свою актуальность.

Основная цель учителя, обучающего математике младших школьников, научить их правильно и быстро вычислять. Причем не важно, как они будут это делать. Важен только результат.

Нужно заметить, что к одним и тем же вычислительным случаям можно применять разные вычислительные приемы. Например, при вычитании 5 из 12 первый прием будет заключаться в следующем: необходимо вычесть столько, чтобы получилось 10.

12 – 5 = 12 - (2 + 3) = (12 - 2) - 3 = 10 – 3 = 7. Анализируя этот случай, убеждаемся, что дети:

1) вначале догадываются о том, что для получения числа 10 надо от 12 отнять 2, т. к. от 10 потом легко отнимать;

2) затем раскладывают число 5: 5 это 2 и еще сколько?

Нужно найти второе число;

5

/ \

2 ?

3) из 10 вычитают 3. Получают 7.

Таким образом, здесь приходится выполнить три операции. А учителю необходимо составить систему заданий к каждой из названных операций.

Покажем второй прием: данное число 12 нужно разложить на сумму чисел так, чтобы одно из слагаемых было 5. здесь детям необходимо знать состав числа 12.

12

/ \

5 и 7

На основе связи сложения и вычитания делаем вывод, что 12 – 5 = 7. В основе взаимосвязи между компонентами и результатами сложения и вычитания лежит осознание учащимися предметного смысла этих действий. Н.Б. Истомина в своем пособии провела глубокий анализ данного этапа изучения арифметических действий.

Результаты вычислительных случаев, относящихся к табличным вычислениям, учащиеся должны выучить наизусть. В остальных случаях учащиеся должны уметь пользоваться специальными вычислительными приемами. Покажем эти внетабличные случаи, которые тоже группируются по сходству вычислительных приемов.

А) Сложение и вычитание целыми десятками

50 ± 30.

Вычисление в подобных случаях сводится к сложению и вычитанию в пределах 10: 50 + 30. 50 – это 5 десятков, 30 – это 3 десятка. 5 десятков и 3 десятка будет 8 десятков. 8 десятков – это 80. Значит, 50 + 30 = 80. Аналогично для вычитания.

Для освоения этого приема школьник должен:

- хорошо представлять десятичный состав двузначного числа. Рассматривая 50 как 5 десятков и 30 как 3 десятка;

- знать таблицу сложения и вычитания в пределах десяти;

- иметь представление о том, как n дес. представить в виде числа n0. В рассматриваемом случае 8 десятков рассматривается как 80 и записывается результат вычислений.

Основные виды заданий, помогающих школьнику освоить данный прием:

1. Вычисли: 40 + 20 = 4дес. + 2 дес. =

2. Вычисли: 6 дес. + 1 дес. = 5 дес. + 3 дес. = 4 дес. - 1 дес. =

3. Вычисли: 7 + 2 = 70 + 20 =

5 – 3 = 5 дес. - 3 дес. =

4. Вставь числа в окошки, чтобы получились верные равенства:

4 + 2 = 6 - 4 =   - 10 = 30

40 + 20 =  60 - 40 =  80 -  = 10

50 +  = 90  + 60 = 70

5. Какое значение может принимать значок в каждой записи?

* + 3 = 8 6-...= 1

* -? ... - ?

6. Сравни выражения:

60 – 20 60 - 10 60 + 20 60 + 10

70+ 10... 10 + 70 90 - 60 ... 70 - 60

7. Вычисли:

40 + 50 - 70 = ... 50 - 40 + 90 = ... 80 - 70 + 20 = ...

Б) Прибавление единиц или десятков к числу

без перехода через десяток

34 + 2; 34 + 20. Теоретической основой в этом случае является свойство прибавления числа к сумме (единицы складываются с единицами, десятки с десятками). В подобных вычислительных случаях первое слагаемое заменяют суммой разрядных слагаемых и к сумме прибавляют число. Это и есть прием.

34 + 2 = (30 + 4) + 2 = 30 + 6 = 36

34 + 26 =?

Для освоения этого приема учащийся должен:

- хорошо представлять разрядный состав двузначных чисел;

- уметь выполнять сложение целых десятков, сложение в пределах десяти и разрядное сложение (50 + 4).

Виды заданий, помогающих ребенку освоить данный прием:

1. Найди ответ к данным примерам среди чисел, записанных ниже, и покажи его стрелкой:

6 + 3 =... 5 + 7 =... 6 + 2 = ...

8, 7, 6, 5, 1, 9, 10, 11, 12.

2. Сравни выражения:

10 + 2... 10 + 20; 56 + 30 ... 56 + 3; 63 + 30 ...63 + 3

3. Выполни действия по образцу:

40 = 30+10; 50 = … + …, и другие задания.

В) Прибавление единиц к числу с получением целого десятка,

влекущего к увеличению разрядных единиц на одну в разряде десятков

34 + 6. Как и в предыдущем случае, теоретической основой является правило прибавления числа к сумме.

34 + 6 = (30 + 4) + 6 = 30 + (4 + 6) = 30 + 10 = 40

Для освоения данного приема школьник должен:

- знать разрядный состав числа;

- уметь складывать в пределах 10;

- уметь выполнять прибавление десяти к целым десяткам.

В школьных учебниках приводится множество различных заданий для усвоения учащимися приведенного приема.

Г) Вычитание единиц или десятков из числа

без перехода через десяток

34 – 2; 34 – 20. Теоретическая основа - вычитание числа из суммы. Прием вычисления тот же самый. Внимание учащихся обращается на правило, что десятки вычитаются из десятков, единицы из единиц.

34 – 2 = (30 + 4) – 2 = 30 + (4 – 2) = 32

34 – 20 = (30 + 4) – 20 = 10 + 4 = 14

Для освоения данного приема школьник должен:

- знать разрядный состав чисел;

- уметь вычитать в пределах десяти;

- уметь выполнять нумерационное сложение.

Д) Вычитание единиц из целых десятков

30 – 6

Легче 6 вычитать из 10, поэтому представим 30 как сумму чисел 20 и 10. 10 – 6 будет 4. 4 да 20 будет 24

Для освоения данного приема ребенок должен знать десятичный состав целых чисел, уметь вычитать в пределах 10 и выполнять разрядное (нумерационное) сложение (20 + 4).

30 – 6 = (20+ 10) – 6 = 20 + 4 = 24

Е) Прибавление единиц к числу

с переходом через десяток

17 + 5. Этот прием имеет два способа вычисления. Покажем их.

Если теоретической основой является прибавление суммы к числу. Прием заключается в том, что второе слагаемое заменяется суммой удобных слагаемых.

17 + 5 =17 + (3 + 2) = 20 + 2 = 22

Если в качестве теоретической основы взять прибавление числа к сумме, то получаем:

17 + 5 = (10 + 7) + 5 = 10 + (7 + 5) = 10 + 12 = 10 + (10 + 2) = 20 + 2 = 22

Для освоения данного приема школьник должен:

- знать состав однозначных чисел:

уметь дополнять любое двузначное число до ближайшего целого;

- уметь выполнять разрядное сложение (20 + 2).

Ж) Сложение двузначных чисел

без перехода через десяток

40 + 16, 45 + 32.

40 + 16 = 40 + (10 + 6) = 50 + 6 = 56

45 + 32 = 45 + (30 + 2) = 75 + 2 = 77

Для освоения данного приема ребенок должен:

- знать разрядный состав двузначных чисел;

- уметь выполнять сложение разрядных единиц (десятки с десятками, единицы с единицами).

З). Вычитание единиц из числа

с переходом через десяток

25 – 7.

В этом случае можно привести два способа вычисления.

1) Если в качестве теоретической основы взять вычитание суммы из числа, то получим: 25 - 7 = 25 – (5 + 2) = 20 – 2 = 18

2) Если в качестве теоретической основы положить вычитание числа из суммы, рассуждая, что из 10 легко вычесть 7, то получим:

25 – 7 = (15 + 10) – 7 = 15 + (10 – 7) = 15 + 3 = 18

Для освоения данного приема ученик должен:

- знать состав однозначных чисел;

- уметь выделять десяток из любого двузначного числа;

- уметь вычитать в пределах 10;

- выполнять разрядное сложение или сложение без перехода через десяток.

И) Вычитание двузначных чисел

без перехода через десяток

65 – 23. Этот вычислительный случай тоже имеет несколько решений. Покажем их.

1) В качестве теоретической основы можно взять вычитание сумму из суммы, тогда получаем:

65 – 23 = (60 + 5) – (20 + 3) = (60 – 20) + (5 – 3) = 40 + 2 = 42.

2) Если теоретической основой будет вычитание суммы из числа, то имеем:

65 – 23 = 65 – (20 + 3) = (65 – 20) – 3 = 45 - 3 = 42.

К) Вычитание двузначного числа из целых десятков

60 – 23. В качестве теоретической основы здесь может быт вычитание суммы из числа, тогда получаем:

60 – 23 = 60 – (20 + 3) =40 – 3 = 37

Прием является сложным. Для его выполнения требуется выполнить ступенчатые «расщепления» числа 40, последовательно занимая десятки для вычитания сначала 20, затем 3.

Л) Сложение двузначных чисел

с переходом через десяток

27 + 58. В качестве теоретической основы возьмем прибавление суммы к сумме. При выполнении данного вычисления в уме (устно) каждое число раскладывается на разрядные составляющие, а затем разрядные единицы складываются: десятки с десятками, единицы с единицами. Получившиеся суммы снова складываются.

27 + 58 = (20 + 7) + (50 + 8) = (20 + 50) + (7 + 8) = 70 + 15 = 85

Для успешного выполнения этого приема ученик должен:

- знать разрядный состав двузначных чисел;

- уметь складывать целые десятки;

- знать таблицу сложения;

- уметь складывать десятки и однозначные числа.

М) Сложение двузначных чисел

с получением в результате целых десятков.

27 + 63

Теоретическая основа та же, поэтому способ выполнения тот же. При устном выполнении данный случай не вызывает затруднений

27 + 63 = (20 + 7) + (60 + 3) = (20 + 60) + (7 + 3) = 80 + 10 = 90

Выполнение этого вычисления требует тех же знаний и умений что и предыдущего.

Н) Вычитание двузначных чисел

с переходом через десяток.

63 – 27. Теоретической основой таких случаев является вычитание суммы из числа. Здесь используется прием – вычитаемое заменяют суммой удобных слагаемых.

63 – 27 = 63 – (20 + 7) = (63 – 20) – 7 = 43 – 7 = 43 – (3 + 4) = (43 – 3)- 4 = 40 – 4 = 36

О) Письменные вычисления

₊36 _56 ₊34 _56 –27

62 23 68 27 63

Видим, что этот случай вычислений отличается записью от других вычислительных случаев, так как различают письменные и устные вычисления. Теоретическая основа – прибавление суммы к сумме, или вычитание суммы из суммы. Письменные вычисления опираются на поразрядное сложение, начиная с низшего разряда. Для вычитания - поразрядное вычитание. Перед каждой группой вычислений учитель знакомит учащихся с правилом, но строго у младших школьников его не спрашивает. Рассуждения вычислений постепенно сворачиваются.

Увлекаться подробными записями не нужно, лучше, если учащиеся проговаривают устно ход мыслей.

Покажем различия устных и письменных вычислений.

Таблица

Различия устных и письменных вычислений

Устные вычисления	Письменные вычисления
Форма записи
В строчку или не записывают	В столбик.
Промежуточные результаты
Сохраняются в памяти или записываются в строчку	Сразу записываются
Способы вычисления
Можно использовать разные способы, например: 25 + 7 = (25 + 5) + 2 = 20 + (5 + 7)… или 25 + 7 = 20 + (5 + 7) = 20 + 12 = и т.д.	Устанавливается специальный алгоритм вычислений (система правил, которые выполняются в определенной последовательности)
Порядок выполнения действий
Действия начинают выполнять со старших разрядов: 48 : 4 = 40 : 4 + 8 : 4.	Письменные вычисления начинают выполнять с единиц (за исключением деления)

Сейчас письменные примы сложения и вычитания вводятся в концентре «Сотня», часть примеров решается устно, часть письменно. Если хотя бы одно из чисел оканчивается 0, и если одно из чисел однозначное, то объяснение ведется с помощью устных приемов, примеры вида 53+21 могут решаться как при помощи приемов устных вычислений (что очень хорошо!), так и в столбик.

Прежде чем вводить письменный прием вычисления, учащимся предлагается устный способ вычислений:

45 + 23 = (40 + 5) + (20 + 3) = (40 + 20) + (5 + 3) = 60 + 8 = 68. Затем отмечается, что удобно записать этот пример столбиком и приводятся подробные объяснения приема вычислений:

1. Пишу десятки под десятками, а единицы под единицами.

2. Складываю единицы: 5 + 3 = 8. Пишу 8 под единицами.

3. Складываю десятки: 4 + 2 = 6. Пишу 6 под десятками.

4. Читаю ответ: сумма равна 68.

Алгоритм письменного вычитания строится на тех же принципах. Сначала школьников знакомят со способом записи чисел при выполнении письменных вычислений и определяют порядок выполнения вычислений (справа налево, начиная с разрядных единиц).

В последнем случае при письменном выполнении школьник может при сложении терять разрядную единицу, так как действия начинают выполнять с разряда единиц и вновь полученную разрядную единицу следует добавить дополнительно к сумме десятков.

Наиболее трудными для учащихся являются случаи вида 70 – 58 и 77 – 58, где для выполнения вычислений необходимо занять десятки из старшего разряда.

1. Пишу единицы под единицами, десятки под десятками.

2. Вычитаю единицы. Из 0 нельзя вычесть 8. Занимаю 1 дес. из 7 дес. Ставлю точку над 7 десятками, чтобы не забыть

1 дес. = 10; 10 - 8 = 2. Пишу под единицами 2.

3. Вычитаю десятки. Было 7 дес., но 1 дес. заняли при вычитании единиц. Осталось 6 дес. 6 дес. - 5 дес. = 1 дес. Пишу 1 под десятками.

4. Читаю ответ: разность равна 12.

Для того чтобы не забыть о единице, которую заняли, над разрядом десятков можно ставить точку, как показано в комментировании приведенного примера, а можно - черточку, или подписывать число, которое осталось после того, как заняли разрядную единицу.

Можно дать следующее обоснование знакомству учащихся второго класса со способами письменных вычислений при формировании вычислительной деятельности в пределах 100:

1. Многие дети с большим трудом осваивают устные вычислительные действия с двузначными числами. Письменный прием вычислений облегчает им вычислительную деятельность.

2. Полноценное освоение устной вычислительной деятельности требует от ребенка свободного владения результатами табличных вычислений в пределах 10 и 20, свободного владения разрядным составом чисел, десятичным составом чисел, умением гибко и свободно применять разнообразные вычислительные действия, выбирая способ вычислений в каждом случае. Далеко не все дети могут это делать. Письменный способ вычислений требует более простых вычислительных действий, выполняемых по единому правилу (называемому «алгоритмом письменных вычислений»).

3. При изучении вычислений в пределах 100 знакомство со способами оформления вычислений «в столбик» рассматривается как подготовка к использованию этих вычислительных приемов в дальнейшем: при вычислениях с трехзначными и многозначными числами.

Наглядными пособиями могут служить палочки и пучки, полоски с изображением десятка (кружками), и единиц, кружки на резинке, абак.