4.3. Неперервність функції

4.3.1. Основні поняття

Означення (Коші)

Функція у = f(x) називається неперервною в точ­ці х0 функцією, якщо ця функція f визначена в точці х0 і для кожного (достатньо малого) числа існує число , таке що при виконується

або

f(x) — неперервна в точці х0, якщо .

Відношення можна переписати у вигляді

Графічна ілюстрація

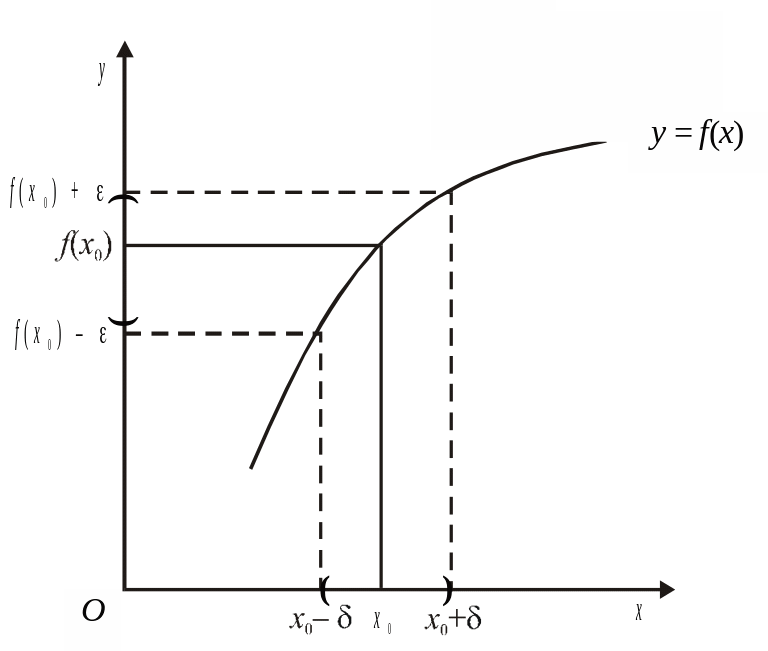
Рис. 4.9

Пояснення. Функція y = f(x) — неперервна в точці х₀, якщо при будь-якому х з інтервалу значення f(x) лежать у смузі .

Дамо означення неперервності функції, еквівалентні означенню Коші

Означення. Функція y = f(x) називається неперервною в точці х₀, якщо

1. f(x) визначена в точці х₀;

2. границя зліва в точці х₀ дорівнює границі справа в цій точці і дорівнює значенню в ній функції (рис. 4.10):

.

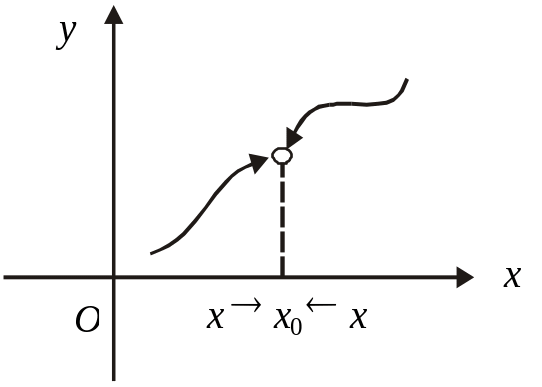
Рис. 4.10

Означення. Функція у = f(x) називається неперервною в точці х₀, якщо нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції .

Приклад. Довести за означенням, що функції y = x² і y = sin x неперервні в будь-якій точці х₀  R.

 1. Надамо аргументу х₀  R приросту х, тоді .

Якщо х — нескінченно мала величина, то у — також нескінченно мала величина, оскільки коли х  0, то і у  0. Отже, y = x²— неперервна функція при будь-якому х₀  R.

2. Надамо аргументу х₀  R приросту х:

Якщо х  0, то у  0. Отже, функція y = sin x неперервна функція при будь-якому х₀  R.

Означення. Функція у = f(x) неперервна на проміжку (а, b), якщо вона неперервна в кожній точці цього проміжку.

Означення. Функція у = f(x) неперервна на відрізку [а, b], якщо вона неперервна на проміжку (а, b) і неперервна в точці х = а справа і в точці х = b зліва.

Означення. Функція у = f(x) називається неперервною в точці х₀ справа (зліва), якщо

Ф ункція

неперервна в точці х₀ зліва (рис. 4.11).

Рис. 4.11

Теорема 1. Усі елементарні функції неперервні на інтервалах визначеності.

4.3.2. Властивості неперервних функцій

Теорема 2. Нехай функції у = f(x) i y = g(x) — неперервні на інтервалі (а, b). Тоді їх наведені далі комбінації також неперервні:

1) F(X)  g(X); 3) const g(X);

2) f(x) g(x); 4) f(x) / g(x), g(x)  0.

Теорема 3. Якщо функція у = f(x) неперервна в будь-якій точці х₀ і u = F(y) неперервна в точці f(x₀), то їх композиція f о F — cкладена функція і u = F(f(x)) — неперервна в точці х₀.

Доведення. За означенням

Д овести, що функція

неперервна в будь-якій точці х.

 Функція у є композицією двох неперервних функцій

і

Функція f(x) і F(x) неперервна згідно з теоремою 1, а їх композиція f о F неперервна за теоремою 3. 

4.3.3. Розриви функції

Означення. Функція у = f(x), яка не є неперервною в точці х₀, називається розривною в цій точці.

Можливі варіанти розриву функцій в точці

(рис. 4.12)

Рис. 4.12

(рис. 4.13).

Рис. 4.13

(рис. 4.14)

Рис. 4.14

Означення.	Точка х0 називається точкою розриву першого роду функції у = f(x), якщо існують скінченні границі і при цьому:
	1.  або 2. або 3. або	неусувний розрив 1-го роду;
	4. — усувний розрив 1-го роду

Означення.

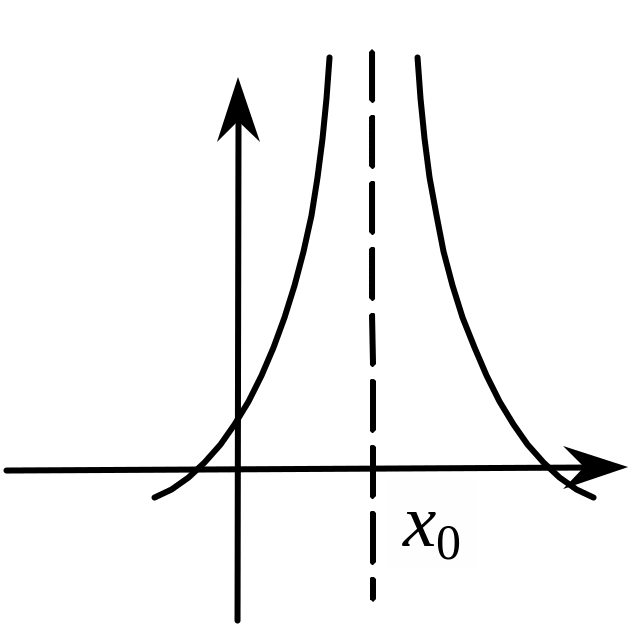
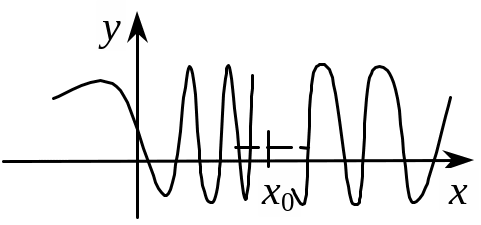
Точка х0 називається точкою розриву 2-го роду функції у = f(x), якщо одна із границь не існує або нескінченна.

4.3.4. Методика дослідження функції у = f(x) на неперервність

1. Знаходимо точку х₀ — «підозрілу» на розрив. Це може бути точка, в якій функція невизначена або змінює закон визначеності.

2. Визначаємо інтервали неперервності функції.

3. Обчислюємо

.

4. Робимо висновок згідно з теоремами (якщо такі границі існують), або використовуючи означення точок розриву.

Д ослідити на неперервність функцію

Рис. 4.15

1. Точка х₀ = 1 є «підозрілою» на розрив, оскільки в ній функція змінює закон визначеності (на проміжку (– ; 1) маємо у = х, на проміжку (1, +) — іншу залежність: у = х + 1).

2. Функція неперервна на проміжках (– ; 1) і (1; + ).

3. Знаходимо

.

4. , тому за означенням функція має в точці х = 1 неусувний розрив 1-го роду.

Д ослідити на неперервність функцію

 1. Точка х₀ = 0 є «підозрілою» на розрив, оскільки в ній функція змінює закон визначеності.

2. (– ; 0) (0; + ) — множина, де функція неперервна.

3. Знаходимо

1 = 1 =1 — функція неперервна в точці х₀ = 0 за означенням неперервної функції. Отже, інтервалом неперервності функції (рис. 4.8).