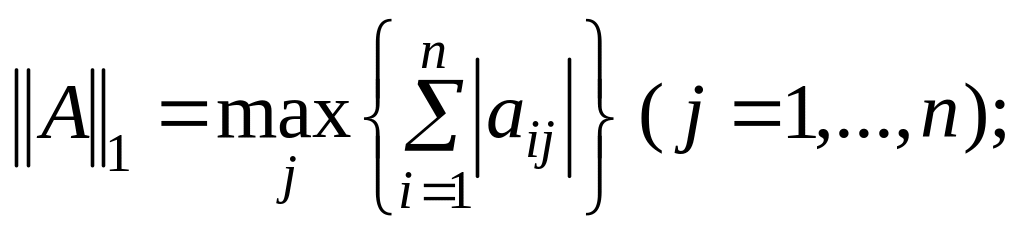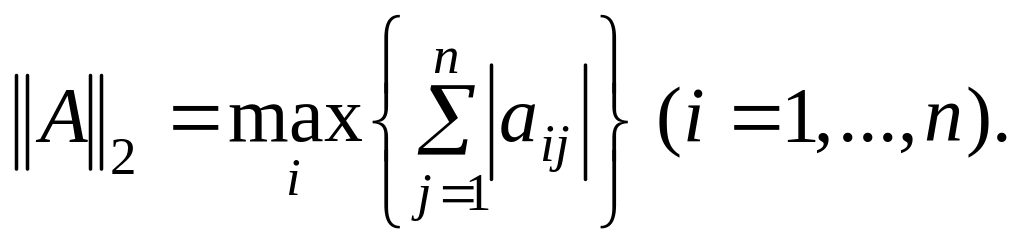2.8. Матриці з домінантною головною діагоналлю

2.8.1. Матриці з комплексними елементами

Для векторів із комплексними проекціями і для матриць із комплексними елементами можна ввести поняття норми. Наведемо деякі означення норми вектора

і відповідної норми матриці

.

Нехай у загальному випадку — комплексні числа. Візьмемо

, ,

(1)

Теорема 1. Усі власні числа матриці А з комплексними елементами лежать у крузі

Доведення. Власний вектор х і власне число задовольняють рівняння

Перейшовши до норм, запишемо рівність

З нерівності випливає:

що й доводить теорему. 

Наслідок. Згідно з (1) доходимо висновку, що всі власні числа матриці А належать кругам:

.

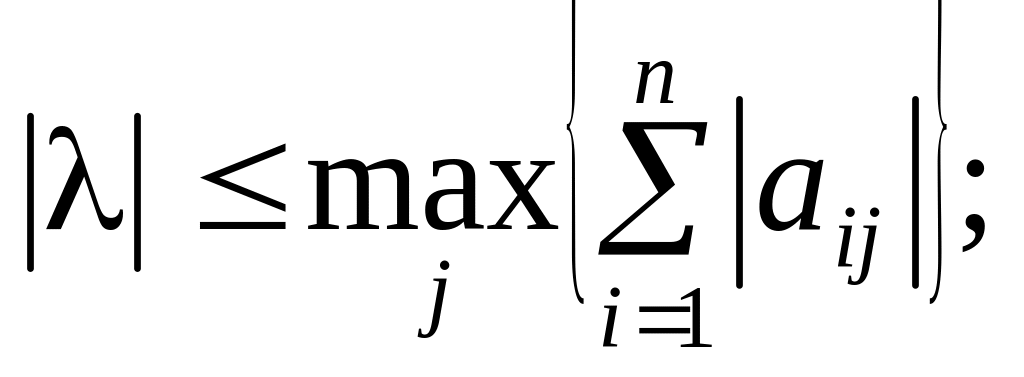
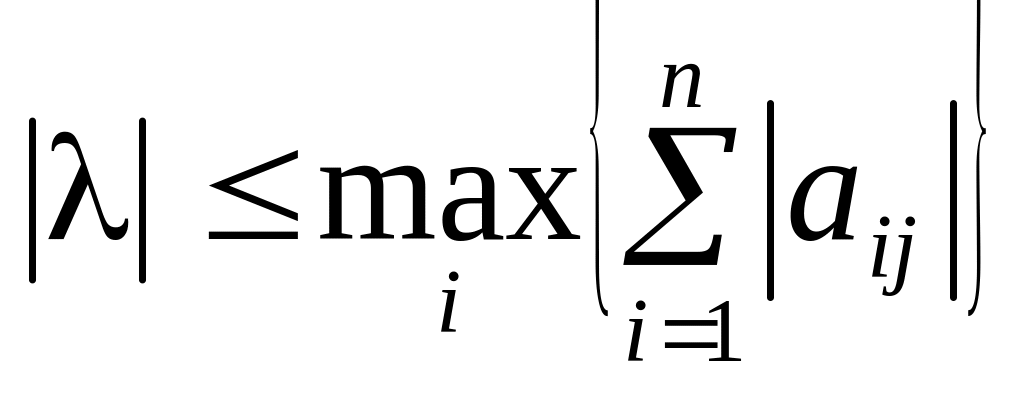
Теорема 2. Якщо , то матриця є неособливою.

Доведення. Характеристичне рівняння

визначає власні числа матриці А. Згідно з теоремою 1 при матриця А (2) власних чисел не має, а тому при рівняння (2) не має розв’язків. Відповідно матриця при є неособливою і має обернену. 

Теорема 3. При виконується рівність

(3)

Доведення. Матричний ряд (3) є збіжним, оскільки виконується нерівність

.

Помноживши ряд на матрицю дістанемо:

Звідси й випливає теорема. 

Наслідок. Якщо , то матриця є неособливою і має обернену:

2.8.2. Матриці з домінантною головною діагоналлю

Означення. Квадратна матриця розміру з комплексними або дійсними елементами називається матрицею з домінантною головною діагоналлю, якщо виконується одна з нерівностей:

(4)

(5)

Якщо виконується нерівність (4), то модулі діагональних елементів більші за суму модулів останніх елементів у рядку. Тому в цьому разі говорять про стовпцеве домінування.

Утворимо діагональну матрицю

і подамо матрицю В у вигляді

або

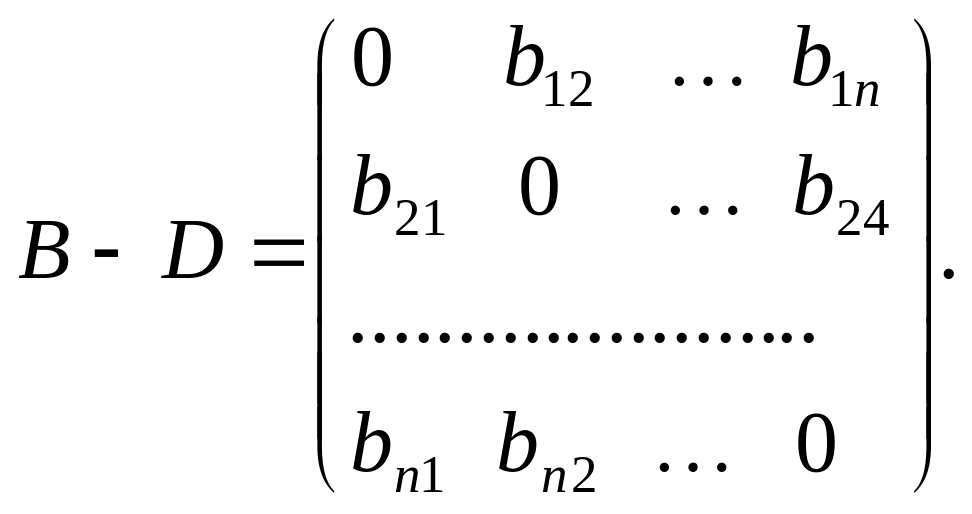
Нехай для матриці В виконуються умови (4). Тоді її можна подати так:

(6)

де

Згідно з (4) та означенням норми (1) маємо нерівність

.

Аналогічно, матрицю В можна подати у вигляді

, (7)

де позначено

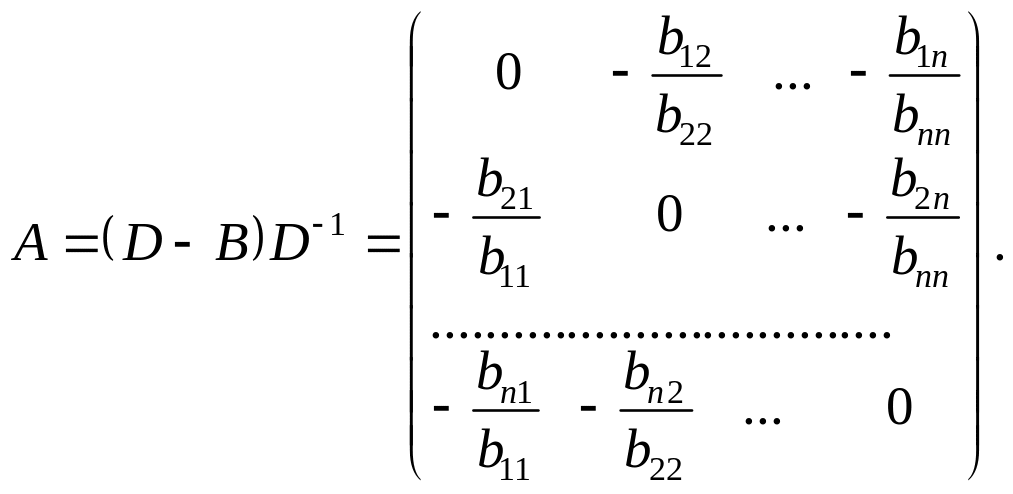
На підставі нерівності (5) за означення норми матриці (1) маємо нерівність

.

Із наслідку теореми 3 випливає теорема Адамара.

Теорема 4. Якщо матриця А розміру має домінантну діагональ, то вона неособлива.

Доведення. Якщо виконується умова (4), то з (6) дістаємо:

Матриця має обернену на підставі нерівності , а діагональна матриця D має обернену матрицю, оскільки її діагональні елементи відмінні від нуля.

Аналогічно розглядається випадок виконання умови (5).

Теорема 5. Якщо матриця А має домінантну від’ємну діагональ, то всі її власні числа мають від’ємні дійсні частини.

Доведення. Розглянемо матрицю . При вона має домінантну діагональ, оскільки

.

Згідно з теоремою 4 матриця є неособливою при , а отже, усі корені характеристичного рівняння

лежать у півплощині 

Наведемо без доведення кілька теорем про властивості матриць із домінантною діагоналлю.

Теорема 6. Нехай для квадратної матриці А справджуються нерівності . Усі власні числа матриці А тоді і лише тоді мають від’ємні дійсні частини, коли матриця А має домінантну від’ємну діагональ.

Теорема 7. Усі власні числа матриці А із невід’ємними елементами тоді і лише тоді лежать в одиничному колі , коли матриця має домінантну додатну діагональ.

Теорема 8. Для того щоб система лінійних алгебраїчних рівнянь

, (8)

де , , для будь-якого додатного вектора мала розв’язок , необхідно і достатньо, щоб матриця А мала домінантну діагональ.

Зауважимо, що систему (8), де матриця А має домінантну діагональ, завжди можна розв’язати методом послідовних наближень, подавши цю систему у вигляді

,

,

зручному для застосування цього методу.