2.3.9. Обернена матриця

Означення. Квадратна матриця А порядку n називається регулярною, або невиродженою, якщо її визначник відмінний від нуля.

Означення. Квадратна матриця А порядку n називається сингулярною, або виродженою, якщо її визначник дорівнює нулю.

У невиродженої матриці всі рядки і стовпці лінійно незалежні. У виродженої матриці рядки і стовпці лінійно залежні.

Теорема 1. Якщо матриця А порядку n невироджена, то для неї існує обернена матриця

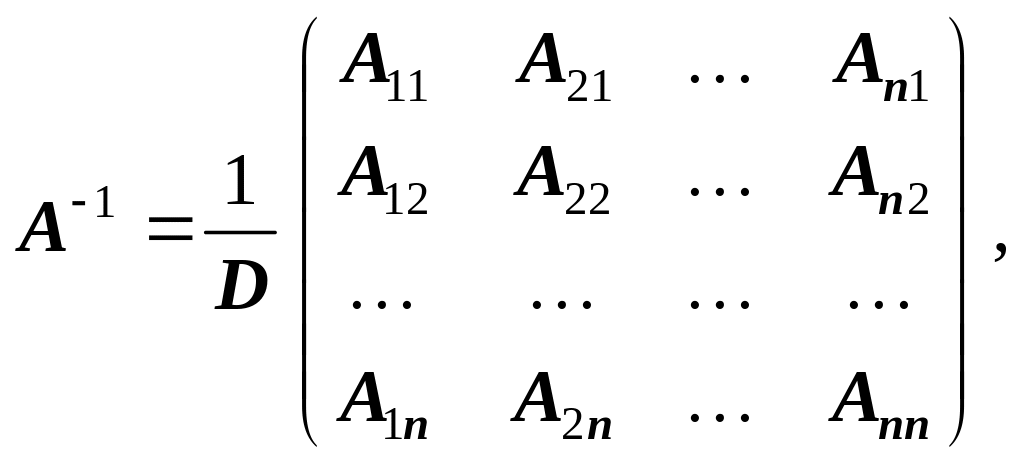(1)

де , а — алгебраїчне доповнення елементів визначника D.

Доведення. Обчислимо добуток матриць

.

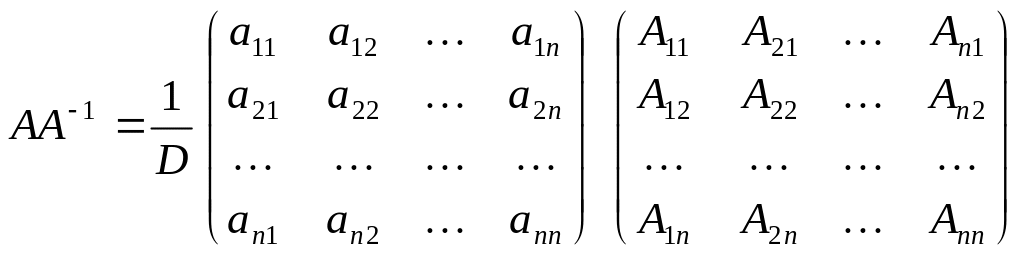Згідно з властивостями 9 і 10 визначників маємо:

звідки АА^–1 = Е, що й доводить теорему. 

З найдемо матрицю, обернену до матриці

  За формулою (1) обчислимо обернену матрицю:

.

З найдемо матрицю, обернену до матриці

.

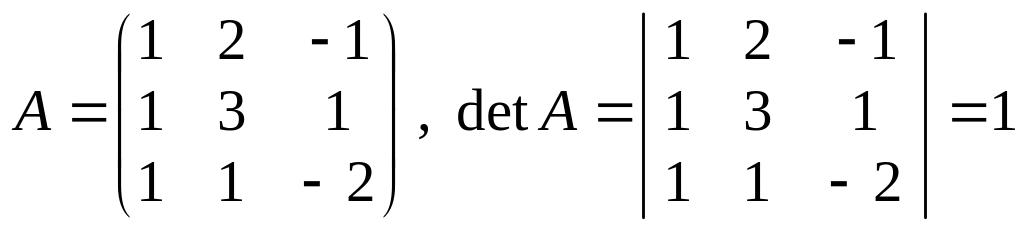Запишемо алгебраїчні доповнення всіх елементів визначника:

;

;

.

Отже, згідно з (1) дістанемо обернену матрицю

.

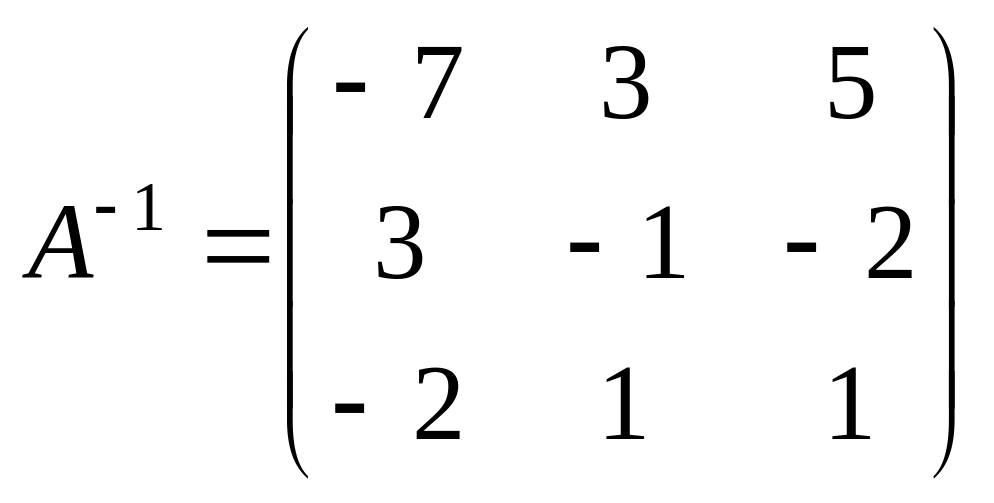Розглянемо деякі найважливіші властивості оберненої матриці.

1. Матриця А^–1 є регулярною, оскільки при det A  0 справджується рівність

.

2. (А^Т)^–1 = (А^–1)^Т. Справді, з рівності

випливає (А^Т)^–1 = (А^–1)^Т.

Якщо матриця А симетрична, то А^–1 = (А^–1)^Т = (А^Т)^–1.

Для ортогональної матриці В маємо рівність ВВ^Т = Е, звідки В^–1 = В^Т.

3. (АВ)^–1 = В^–1 А^–1. Щоб довести цю властивість, знайдемо добуток

.

У загальному випадку маємо:

.

4. Матриця, обернена до верхньої трикутної матриці, також є верхньою трикутною матрицею. 

Р озглянемо верхню трикутну матрицю А і обернену до неї:

.

Отже, обернена матриця справді є верхньою трикутною.

139