2.3.7. Формули Крамера

Спинимося на застосуванні теорії визначників до розв’язуван­ня системи n лінійних алгебраїчних рівнянь з n невідомими:

(1)

Означення. Визначник, елементами якого є коефіцієнти при невідомих у системі (1)

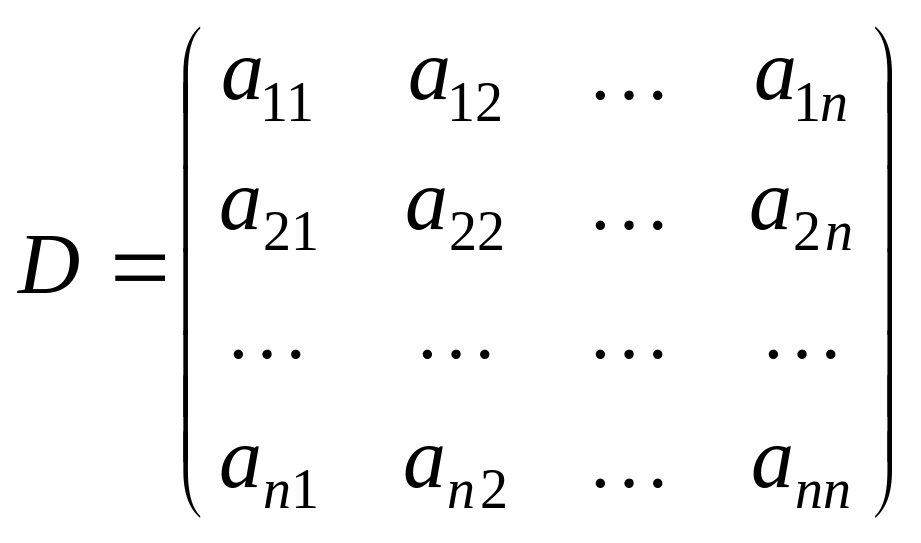, (2)

називається визначником цієї системи.

Теорема. Якщо визначник D системи лінійних алгебраїчних рівнянь (1) відмінний від нуля, то ця система має єдиний розв’язок:

(3)

Тут D_k — визначник, утворений з визначника D системи (1) заміною k-го стовпця на стовпець із правих її частин.

Доведення. Помноживши k-те рівняння системи (1) на алгебраїчне доповнення A_ks елемента а_ks і додавши всі рівняння, дістанемо:

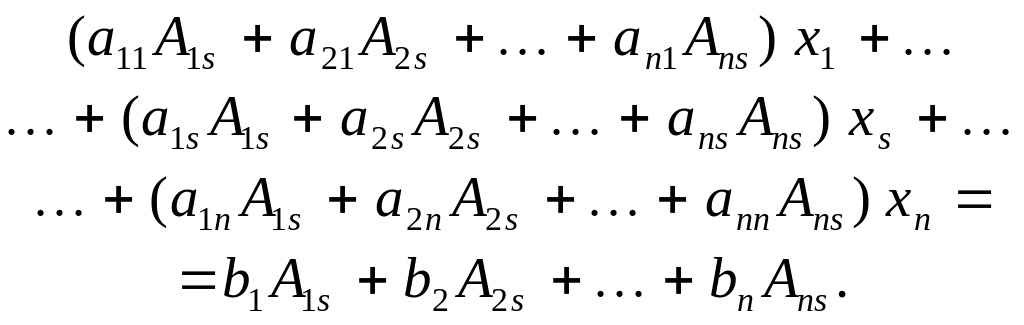
Згідно з властивостями 9 і 10 визначників маємо рівняння

з якого при випливають формули (3).

Отже, якщо система рівнянь (1) має розв’язок, то він подається у вигляді (3).

Доведемо, що ці формули справді визначають розв’язок системи рівнянь (1), підставивши туди розв’язки (3). Для k-го рівняння маємо:

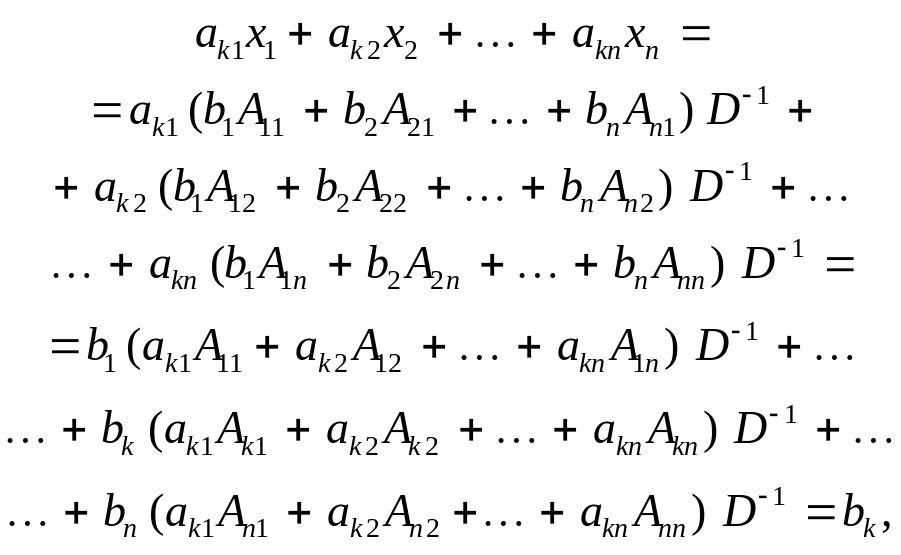
з якого випливає справедливість теореми. 

Р озв’яжемо за формулами Крамера систему рівнянь:

 Запишемо відповідні визначники і знайдемо розв’язки системи рівнянь:

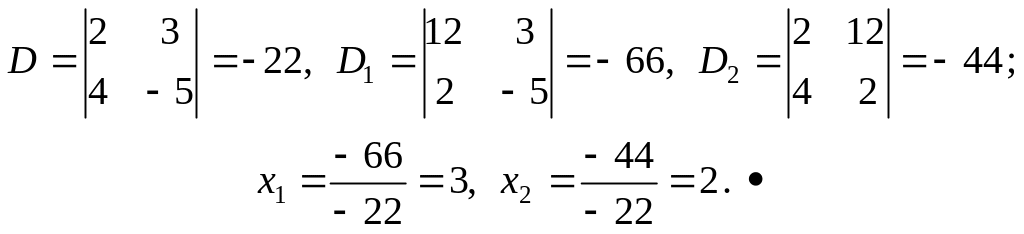
Р озв’яжемо систему рівнянь

 Обчислимо визначник цієї системи:

.

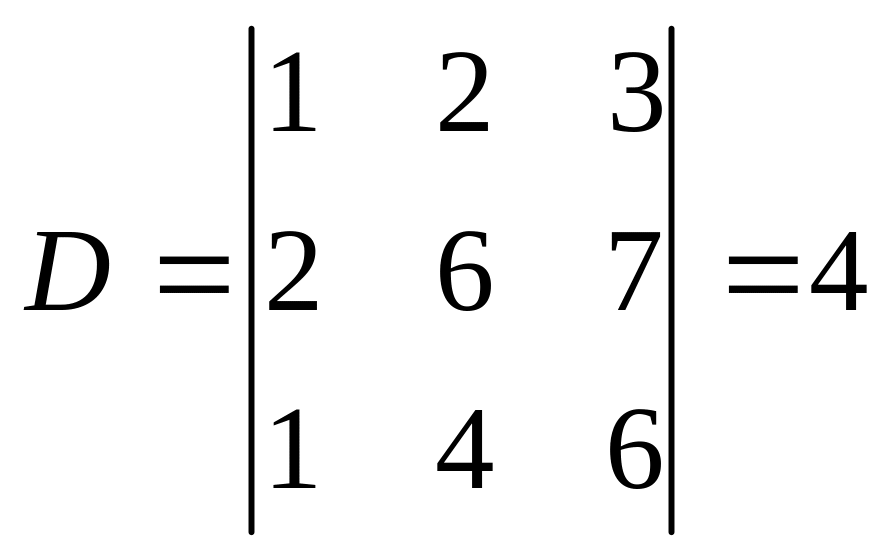Визначник системи відмінний від нуля. Знайдемо тепер визначник і розв’язки системи рівнянь:

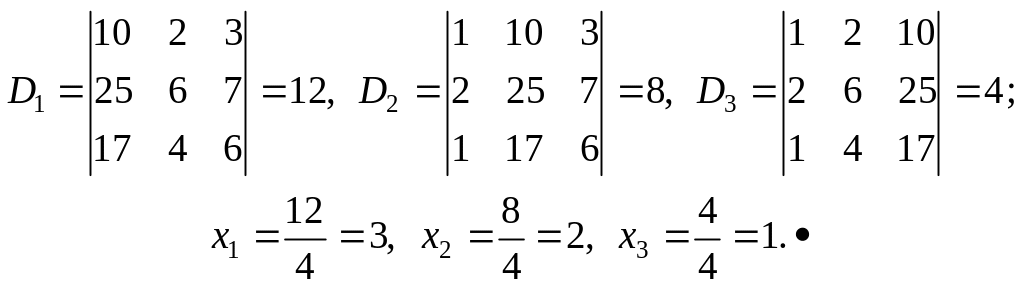
Формули Крамера незручні для практичних обчислень при , але вони застосовуються в теоретичних дослідженнях.

2.3.8. Розв’язування однорідної системи лінійних алгебраїчних рівнянь

Розв’яжемо систему рівнянь

(1)

Ця система завжди сумісна, оскільки має нульові розв’язки

Знайдемо (якщо вони існують) ненульові розв’язки системи (1).

Теорема 1. Якщо визначник D системи рівнянь (1) дорівнює нулю, а серед алгебраїчних доповнень елементів k-го рядка є ненульові, то ця система має ненульовий розв’язок виду

(2)

де t — довільний параметр.

Доведення. Підставимо розв’язок (2) у систему рівнянь (1). При дістанемо

При

,

оскільки D = 0. Теорему доведено. 

З найдемо ненульовий розв’язок однорідної системи лінійних алгебраїчних рівнянь

Обчислимо визначник цієї системи:

.

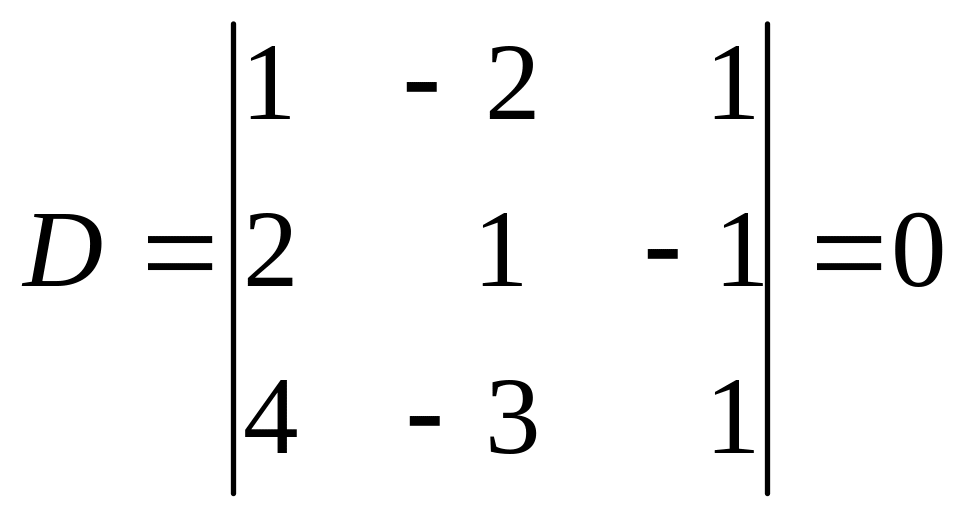Знайдемо алгебраїчне доповнення елементів першого рядка:

.

Система однорідних рівнянь має розв’язок

,

що залежить від довільного параметра. Узявши , дістанемо іншу форму запису розв’язку

де s — довільний параметр.

У загальному випадку справджується така теорема.

Теорема 2. Для того щоб система лінійних однорідних рівнянь (1) мала ненульовий розв’язок, необхідно і достатньо, щоб визначник системи дорівнював нулю.

Цю теорему можна сформулювати в інших термінах.

Теорема 3. Для того щоб вектори

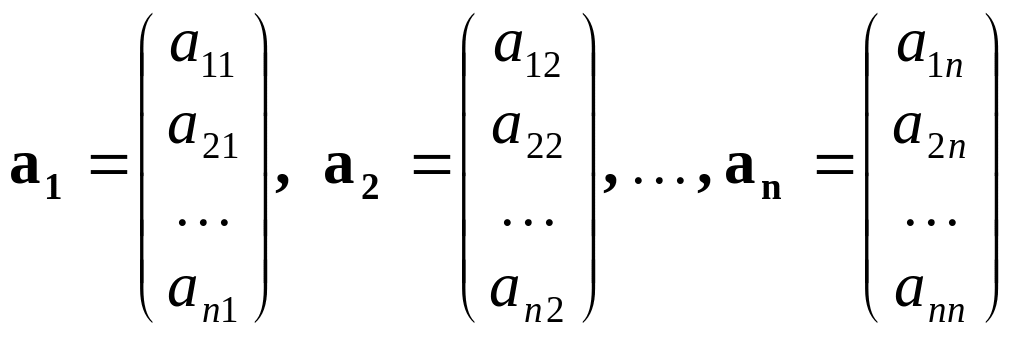
були лінійно залежними, необхідно і достатньо, щоб визначник зі стовпцями дорівнював нулю:

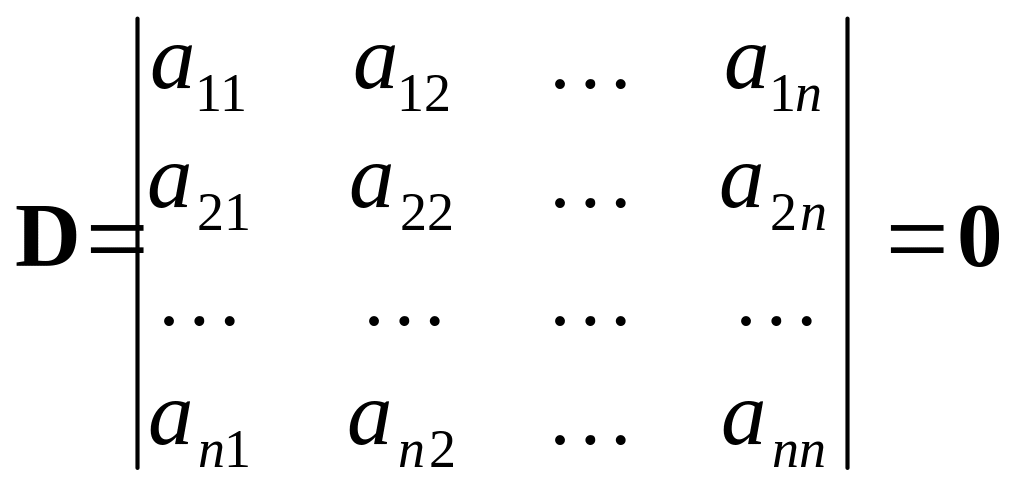. (2)

Доведення. Необхідність очевидна і випливає з того, що при лінійно залежних рядках визначник дорівнює нулю.

Доведемо достатність. Нехай D = 0. Знайдемо найбільший за порядком мінор визначника D, який не дорівнює нулю. Нехай порядок мінора дорівнює k (k < n).

Переставляючи рядки та стовпці, можемо досягти того, щоб мінор, розміщений у верхньому лівому куті, став відмінним від нуля:

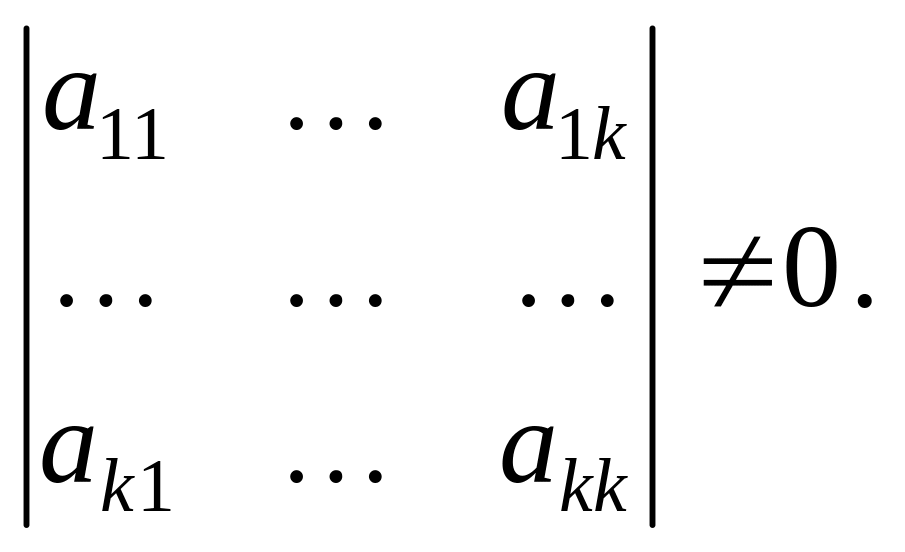(3)

Кожний визначник порядку k + 1 дорівнює нулю. Вектори будуть лінійно незалежними. Доведемо, що решта стовпців являтимуть собою лінійну комбінацію векторів .

Знайдемо розв’язок системи k рівнянь з k невідомими:

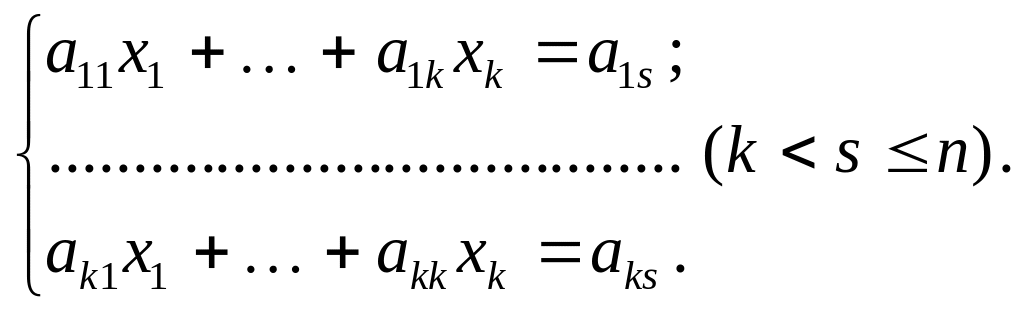(4)

Ця система рівнянь завжди має розв’язок за формулами Крамера згідно з умовами (3).

Розглянемо довільний визначник порядку k + 1

.

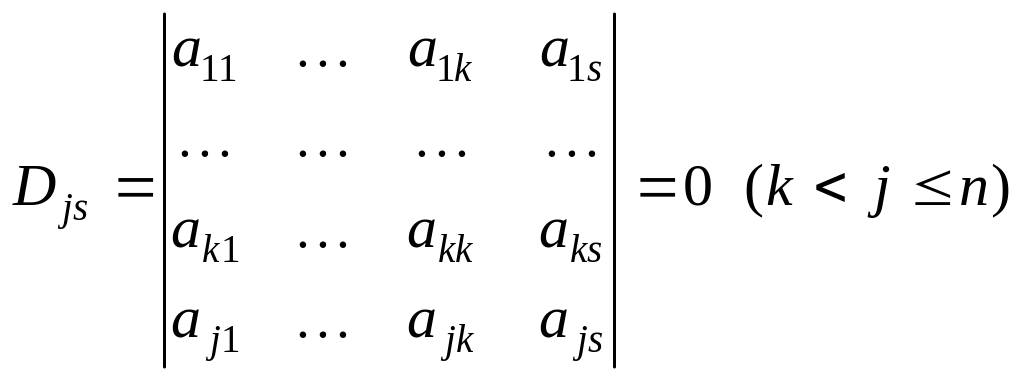Помножимо перший стовпець на х₁, другий — на k-й — на і віднімемо від останнього стовпця. Врахувавши (4), дістанемо визначник

.

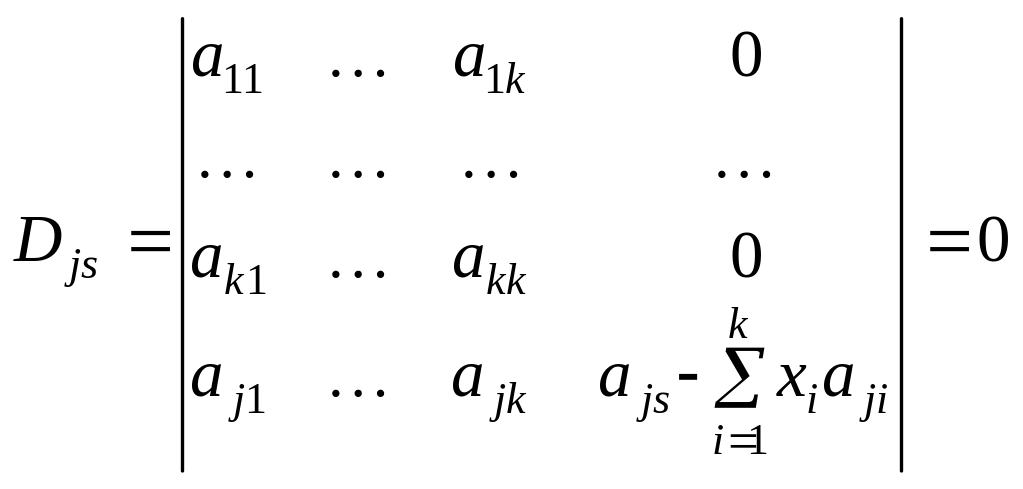Звідси випливає, що виконуються рівності

. (5)

Із системи рівнянь (4), (5) випливає, що будь-який стовпець є лінійною комбінацією стовпців . Отже, ранг системи векторів дорівнює k (k < n), що доводить теорему. 

Система рівнянь (1) має n – k лінійно незалежних ненульових розв’язків.

Міркуючи аналогічно, можна довести таку теорему.

Теорема 4. Ранг матриці А розміру дорівнює найбільшому порядку відмінного від нуля її мінора.

Оскільки значення визначника при транспонуванні не змінюється, то ранг матриці А дорівнює рангу транспонованої матриці А^Т. Отже, справджується теорема.

Теорема 5. Число лінійно незалежних рядків матриці дорівнює числу лінійно незалежних її стовпців.

О бчислимо за допомогою визначників ранг матриці

.

 Матриця має мінор , відмінний від нуля.

Отже, два перші стовпці і два перші рядки матриці А лінійно незалежні. Утворимо визначники третього порядку, які містять зазначений мінор:

.

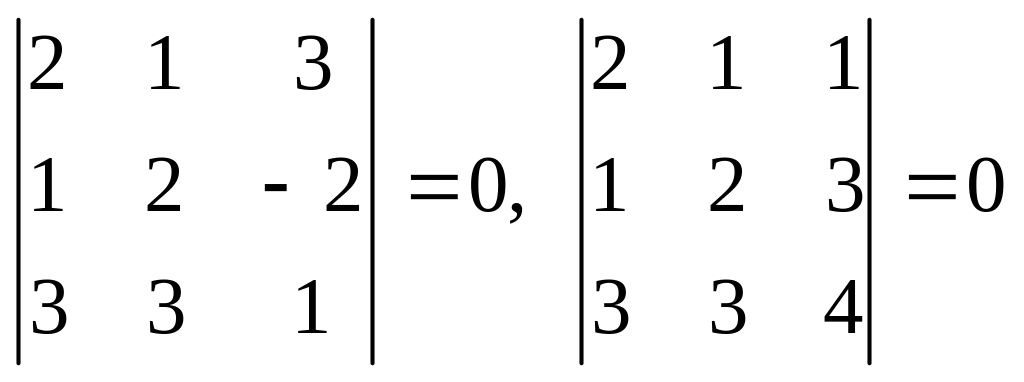Ці визначники дорівнюють нулю, звідки rank A = 2. 

З ауваження. Обчислюючи мінори третього порядку, ми знаходимо значення не всіх можливих мінорів, а лише тих, які містять мінор другого порядку, відмінний від нуля. Цей метод називається методом обвідних мінорів.