2.3.4. Обчислення визначників

Обчислюючи визначники, можна ефективно застосовувати таку теорему.

Теорема 1. Якщо всі елементи визначника, розміщені вище або нижче від головної діагоналі, дорівнюють нулю, то визначник дорівнює добутку діагональних елементів.

Доведення. Єдиним доданком, який може бути відмінним від нуля, є добуток діагональних елементів, оскільки визначник є алгебраїчною сумою добутків його елементів, узятих по одному з кожного рядка та кожного сповпця. Маємо:

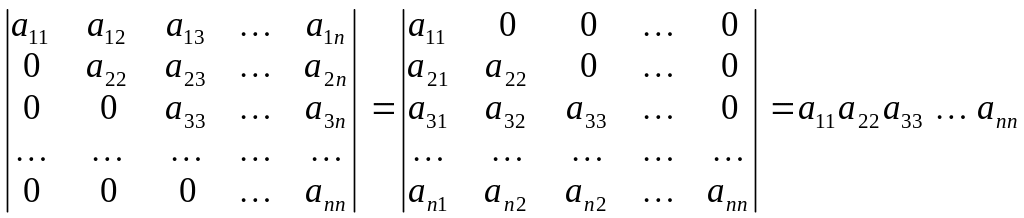. (1)

Щоб перетворити визначник до виду (1), застосуємо властивість 8.

О бчислимо визначник третього порядку

.

 Знайдемо різницю першого і другого рядків, а потім помножимо перший рядок на 2 і віднімемо від третього рядка. Дістанемо визначник

.

Віднявши другий його рядок від третього, дістанемо

. 

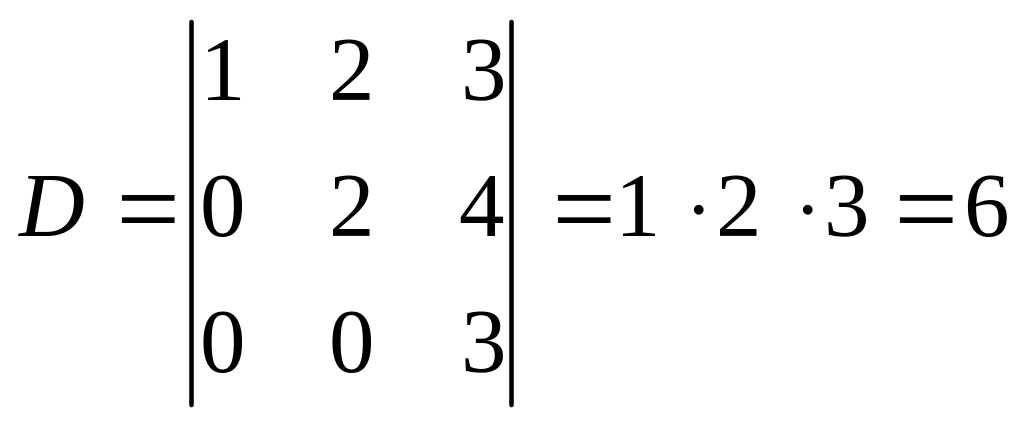О бчислимо визначник четвертого порядку

.

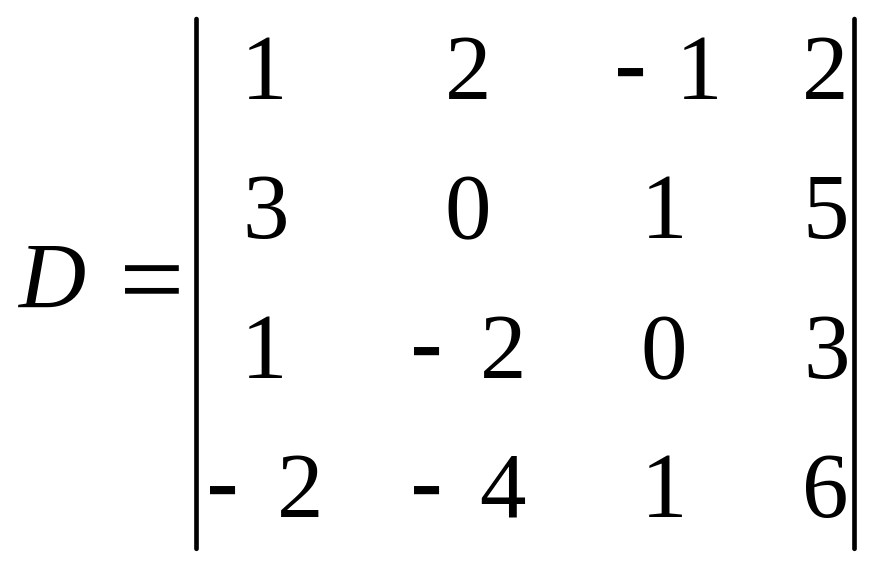 Додамо перший рядок до другого і четвертого, утворивши визначник

.

Поміняємо місцями перший і третій стовпці:

.

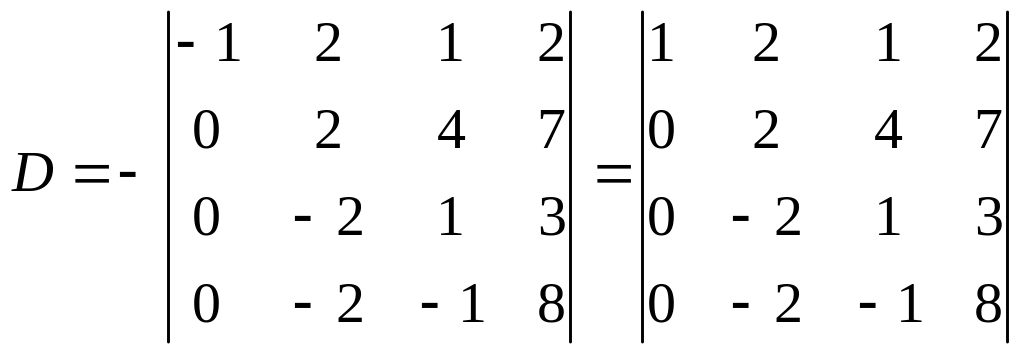Додамо другий рядок до третього і четвертого рядків і винесемо спільний множник елементів третього і четвертого рядків:

.

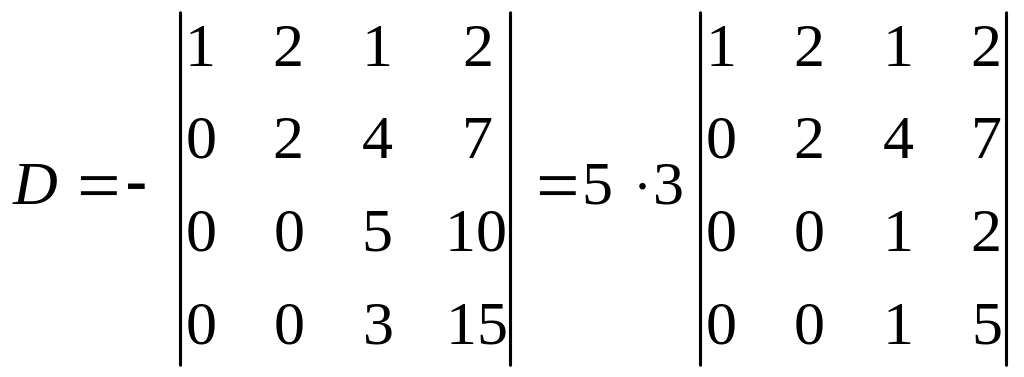Віднявши третій рядок від четвертого, обчислимо даний визначник за формулою (1):

.

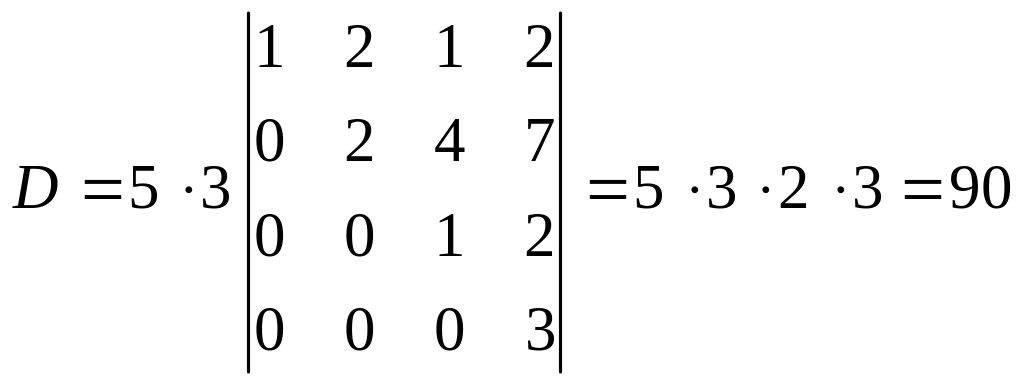2.3.5. Мінори. Алгебраїчні доповнення

Означення. Викреслимо у визначнику n-го порядку k-й рядок і s-й стовпець, а з решти елементів утворимо визначник (n – 1)-го порядку зі збереженням розміщення рядків і стовпців.

Здобутий визначник називається мінором визначника і позначається M_ks.

Визначник, утворений у результаті викреслювання кількох рядків і стовпців даного визначника, також називається його мінором.

З найдемо деякі мінори визначника третього порядку:

.

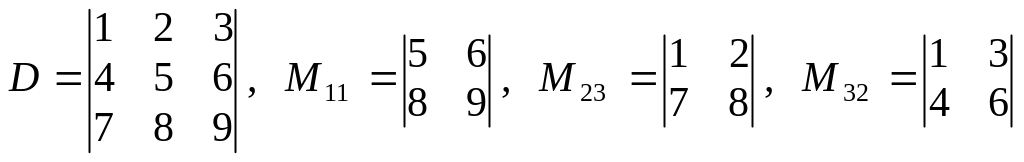Означення. Викреслимо в матриці А розміру m  n кілька рядків і стовпців так, щоб із решти елементів можна було скласти визначник. Цей визначник називається мінором матриці.

Теорема. Алгебраїчне доповнення елемента визначника можна подати у вигляді

(1)

Доведення. Із формули для визначника n-го порядку маємо:

Далі записуємо вираз для алгебраїчного доповнення елемента :

, (2)

де — переставлення виду

.

Оскільки мінор є визначником порядку n – 1, то для нього знаходимо вираз

(3)

де — переставлення чисел :

.

Можна довести, що виконується рівність

.

Нехай перед числом s у переставленні міститься j чисел, менших за s; після числа s міститься s – 1 – j чисел, менших за s. Якщо від переставлення перейдемо до переставлення , то число інверсій зменшиться на .

Отже, виконується рівність

. (4)

Оскільки алгебраїчне доповнення і мінор утворені з одних і тих самих добутків елементів визначника, знаки перед якими або збігаються при , або протилежні при , то дістаємо (1).

З ауваження. Властивість визначників

(j = 1, 2, …, n) може бути покладена в основу теорії визначників і називається розкладом визначника за рядком або за стовпцем (розклад Лапласа).

Р озкладемо визначник четвертого порядку за елементами третього рядка:

або за елементами першого стовпця:

.

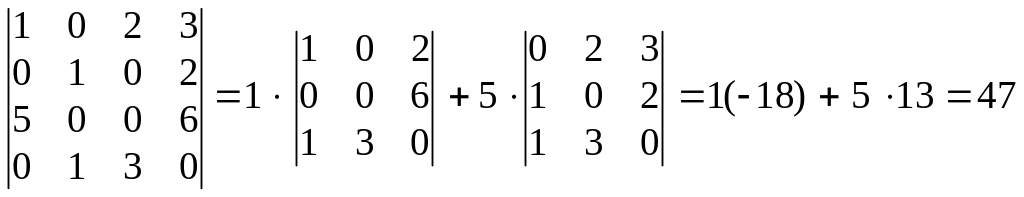2.3.6. Теорема Лапласа

Розглянемо квадратну матрицю

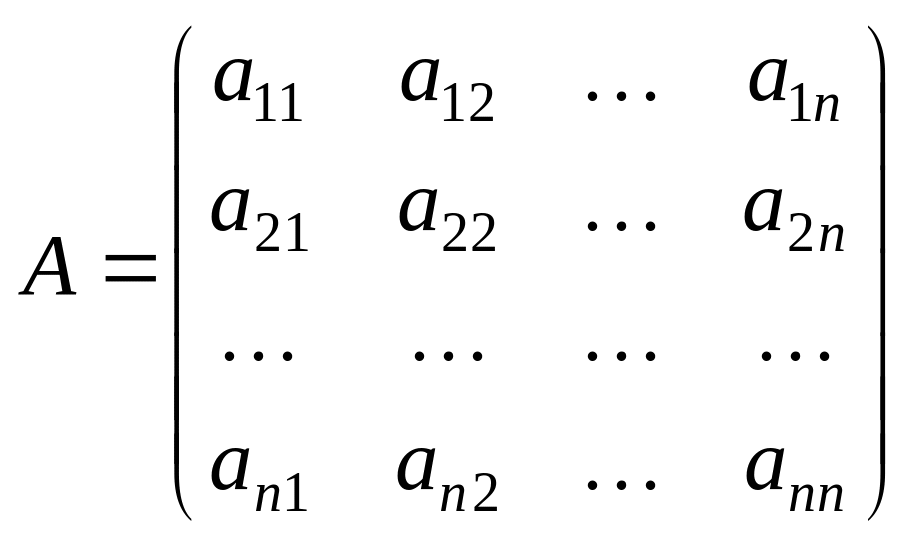
зі стовпцями

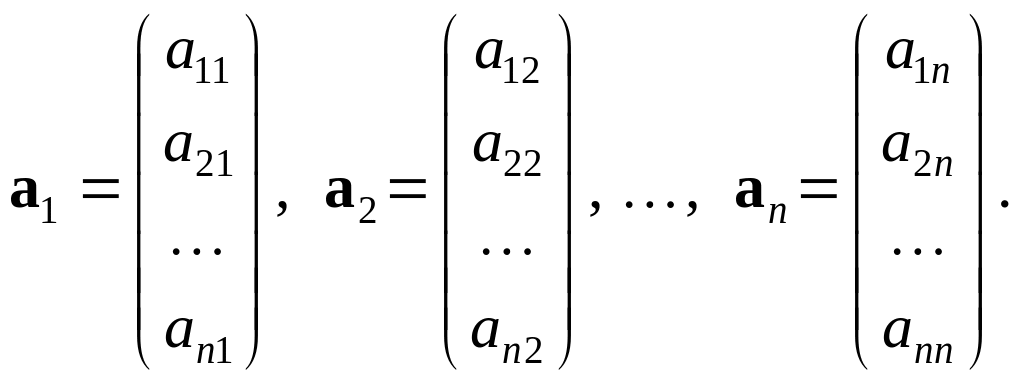
Визначник D матриці А є функцією векторів . Позначимо .

За властивостями визначника маємо, що D є лінійною відносно кожного аргументу функцією:

.

Визначник змінює знак у результаті переставлення векторів:

.

Звідси випливає, що при визначник дорівнює 0, а також що

,

де — переставлення індексів .

Теорема 1. Якщо стовпці (або рядки) матриці А лінійно залежні, то її визначник дорівнює 0.

Доведення. Нехай а_n — лінійна комбінація векторів :

.

Обчислюємо визначник

. 

Запишемо квадратну матрицю порядку n

і знайдемо добуток

.

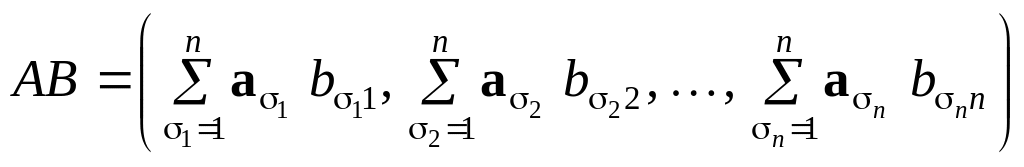Теорема 2. (П. Лаплас). Визначник добутку квадратних матриць дорівнює добутку визначників цих матриць:

Доведення. Згідно з відомими властивостями визначників маємо:

Оскільки справджується рівність

,

дістанемо відому формулу Лапласа:



З найдемо добуток матриць :

та їх визначників:

,

.

Очевидно, формула Лапласа виконується.

Теорема 3. Якщо А — ортогональна матриця, то

.

Доведення. Ортогональна матриця задовольняє умови

,

де Е — одинична матриця. Оскільки , то згідно з теоремою Лапласа

.

У результаті транспонування матриці значення її визначника не змінюється, тобто . Із рівняння

випливає правильність теореми. 