2.3.3. Властивості визначників

Властивість 1. При транспонуванні визначника його значення не змінюється.

Доведення. Доведемо, що визначники

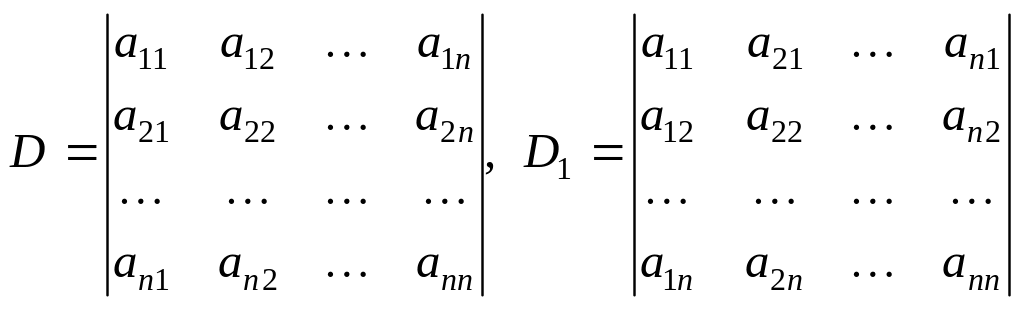
рівні. Розглянемо доданки, які входять до D:

.

Якщо позначити , то до визначника D₁ увійде відповідний доданок

.

Оскільки до визначників D та D₁ входять однакові доданки з однаковими знаками, то D = D₁.

Із властивості 1 випливає, що рядки та стовпці визначника рів­ноправні. Усі наведені далі властивості, що справджуються для рядків, виконуються й для стовпців. 

Д ля визначника другого порядку маємо:

.

Властивість 2. Якщо всі елементи деякого рядка дорівнюють нулю, то визначник дорівнює нулю.

Доведення. Оскільки кожний із доданків, що входять до визнач­ника, містить нульовий множник, то всі доданки дорівнюють нулю і визначник також дорівнює нулю. 

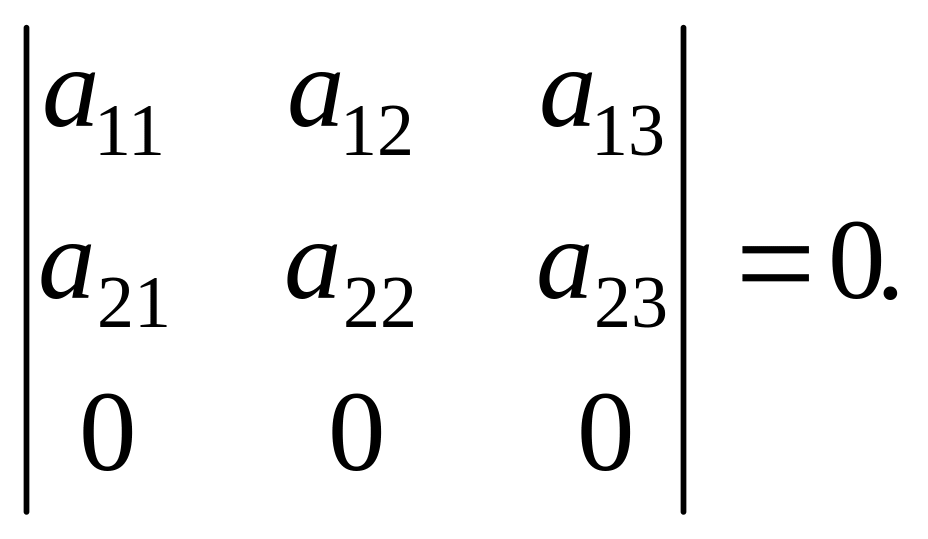
Властивість 3. Якщо всі елементи будь-якого рядка мають спільний множник, то його можна винести за знак визнач­ника.

Доведення. Кожний із доданків, що входять до визначника, містить один із елементів розглядуваного рядка. Тому спільний множник елементів цього рядка можна виносити із суми цих доданків. 

О бчислимо визначник:

.

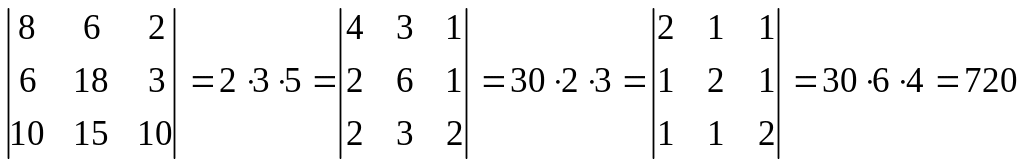Властивість 4. Якщо поміняємо місцями два рядки визначника, то він змінить свій знак.

Доведення. У визначнику n-го порядку поміняємо місцями k-й і s-й рядки (s > k). Здобутий визначник позначимо D₁. Якщо до визначника D входить доданок

,

то до визначника D₁ обов’язково входить аналогічний доданок

.

Оскільки переставлення других індексів відрізняються однією транспозицією, то парність переставлень різна. Отже, доданок, що є добутком розглядуваних елементів, завжди входить до визначників D та D₁ з різними знаками. Це й доводить потрібну властивість. 

П оміняємо місцями рядки у визначнику:

.

Властивість 5. Якщо у визначнику два рядки однакові, то визначник дорівнює нулю.

Доведення. Поміняємо місцями однакові рядки визначника. Він при цьому не зміниться, а згідно з властивістю 4 лише змінить свій знак, тобто D = –D. Звідси випливає, що D = 0. 

Д ля визначника третього порядку виконується рівність:

,

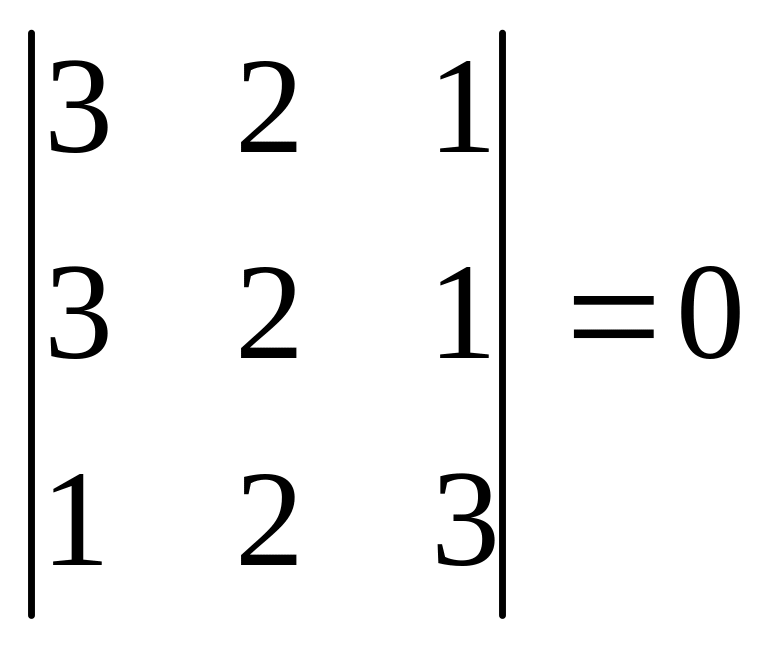оскільки цей визначник має два однакові рядки.

Властивість 6. Якщо у визначнику елементи одного рядка пропорційні до відповідних елементів іншого рядка, то визначник дорівнює нулю.

Доведення. Винесемо множник пропорційності за знак визнач­ника й дістанемо визначник з двома однаковими рядками, який дорівнює нулю. 

Властивість 7. Якщо у визначнику D всі елементи будь-якого рядка є сумою двох доданків, то цей визначник є сумою двох визначників, усі елементи яких (крім фіксованого рядка) збігаються. У першому визначнику фіксований рядок містить перші доданки, у другому визначнику фіксований рядок містить другі доданки.

Доведення. Візьмемо k-й рядок. Оскільки до кожного з доданків, що утворюють визначник, входить один із елементів k-го рядка, то можна в загальному вигляді записати розклад визначника за елементами цього рядка:

.

Множники називаються алгебраїчними доповненнями елементів . Якщо ці елементи є сумами двох доданків то

що й доводить сформульовану властивість. 

З а властивістю 7 маємо:

.

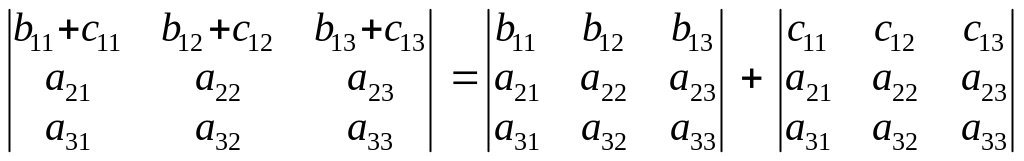Властивість 8. Якщо до елементів деякого рядка визначника додати відповідні елементи іншого його рядка, помноживши на одне й те саме число, то значення визначника при цьому не зміниться.

Доведення. Додамо до елементів k-го рядка визначника D елементи s-го його рядка , помножені на число . Здобутий визначник набере такого вигляду D₁:

Останній доданок дорівнює нулю, бо визначник має однакові k-ті та s-ті рядки. Отже, D₁ = D. 

М аємо рівність визначників:

.

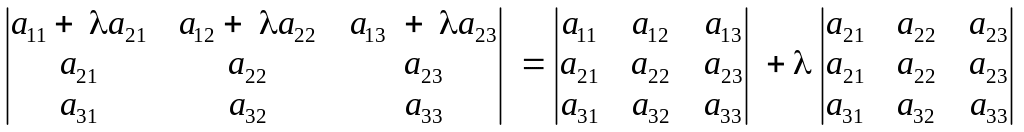Із доведення властивостей 7 і 8 випливають розглянуті далі властивості визначників.

Властивість 9. Сума добутків елементів будь-якого рядка або стовпця визначника на відповідні алгебраїчні доповнення дорівнює цьому визначнику, тобто якщо

,

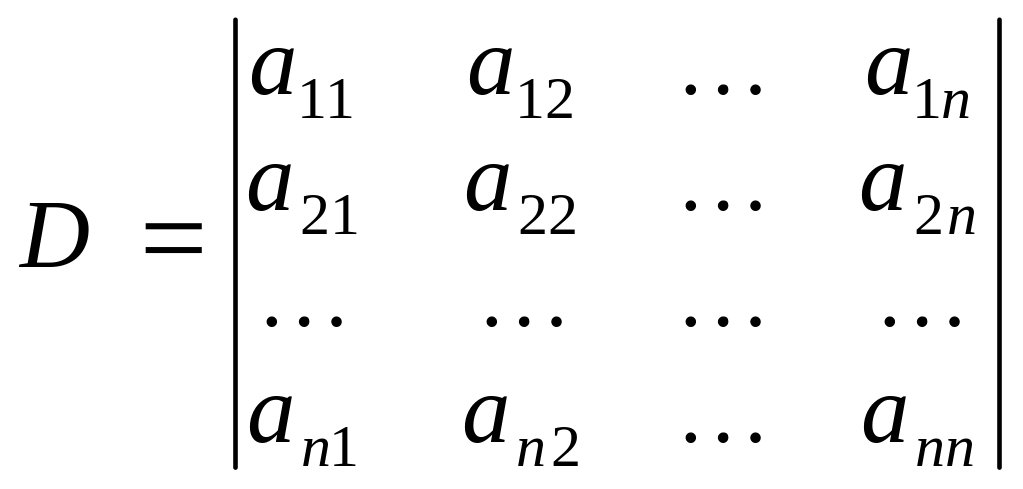то справджуються рівності:

Властивість 10. Сума добутків елементів будь-якого рядка визначника на алгебраїчне доповнення відповідних елементів іншого його рядка дорівнює нулю:

.

Аналогічна властивість виконується для стовпців:

.

Властивості 9 і 10 мають важливе значення, оскільки використовуються при обчисленні алгебраїчних доповнень, про що йтиметься далі.