2.3. Визначники

2.3.1. Парні та непарні переставлення

Означення. Переставленням називається взаємно однозначне відображення множини чисел на себе.

Якщо позначити переставлення виразом

,

то є одним із чисел , і при різних j числа різні.

Числа називаються елементами переставлення.

П ереставлення з трьох чисел 1, 2, 3, що являють собою сукупність

,

є різними, оскільки різняться між собою порядком елементів.

Із записаних шести переставлень лише в першому числа йдуть у натуральному порядку, а в решті цей порядок порушується.

Означення. Коли в переставленні більше число передує меншому, говорять, що ці числа утворюють інверсію.

Переставлення називається парним, якщо загальне число інверсій у ньому парне, і непарним, якщо зазначене число непарне.

П ереставлення — непарне, оскільки містить три інверсії. Переставлення — парне, бо має шість інверсій.

Означення. Транспозицією називається перетворення, у результаті якого міняються місцями лише два елементи переставлення.

Теорема 1. У результаті транспозиції парність переставлення змінюється.

Доведення. Здійснимо транспозицію двох сусідніх елементів переставлення. При цьому парність його змінюється, оскільки число інверсій збільшується або зменшується на одиницю.

Нехай здійснюється транспозиція двох довільних елементів переставлення, між якими містяться ще m елементів. Для розрізнення один з елементів назвемо першим, а інший — другим.

Будь-яку транспозицію можна дістати в результаті транспозицій лише сусідніх елементів.

Справді, поміняємо спочатку місцями перший елемент переставлення із сусідніми проміжними елементами, далі поміняємо місцями перший і другий елементи, а потім послідовно поміняємо місцями другий елемент та m проміжних сусідніх елементів. Тоді другий елемент стане на місце першого. Оскільки транспозиція відбувається в результаті 2m + 1 транспозицій сусідніх елементів, то парність переставлення змінюється.

Надалі, якщо — парне переставлення, вважаємо . Якщо переставлення непарне, .

Теорема 2. Число парних переставлень дорівнює числу непарних переставлень при і становить

Доведення. Нехай N₁ — число непарних переставлень, а N₂ —число парних переставлень. Виконаємо в усіх переставленнях транспозицію елементів 1 і 2. Усі різні парні переставлення перетворяться на різні непарні переставлення, тобто .

Аналогічно дістанемо . Отже, . Оскільки загальне число переставлень із n елементів дорівнює то 

В изначимо парність переставлень трьох чисел 1, 2, 3:

(1)

2.3.2. Означення визначника

Нехай А — квадратна матриця розміру nn:

.

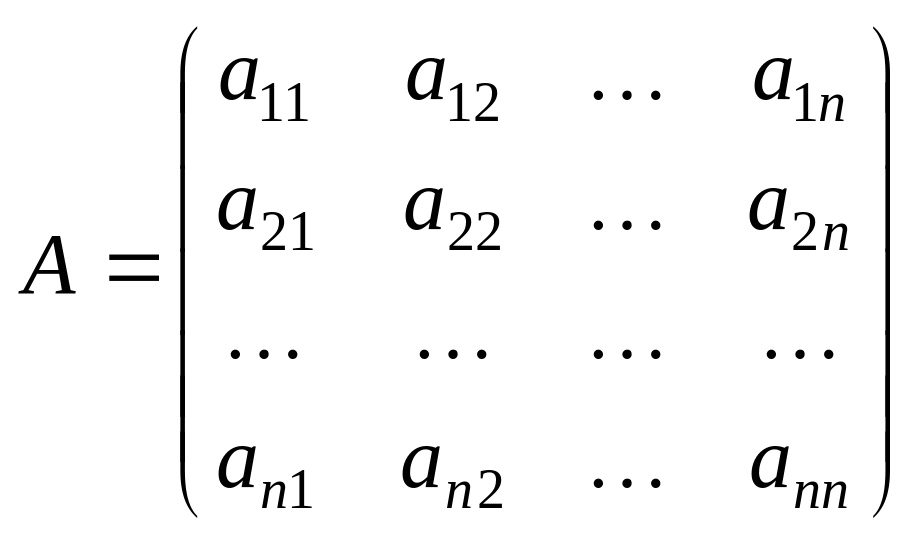Означення. Визначником матриці А n-го порядку називається алгебраїчна сума всіх можливих добутків n елементів матриці, узятих по одному з кожного її рядка і кожного стовпця. Якщо в кожному добутку перші індекси розміщені в порядку зростання, то знак добутку дорівнює (–1)^s, де s — число інверсій у переставленні других індексів.

Визначник подається виразом

(1)

де — переставлення чисел . Вираз (1) називається визначником n-го порядку, числа — його елементами; горизонтальні послідовності чисел називаються рядками визначника, а вертикальні — його стовпцями. Ряд чисел називається головною діагоналлю визначника.

Якщо в (1) переставимо елементи довільним чином, то ця формула набере вигляду

де — переставлення чисел .

Отже, якщо переставлення перших індексів і других індексів мають однакову парність, то відповідний доданок береться зі знаком «+», а якщо різну, то відповідний доданок береться зі знаком «–».

Згідно з цим означенням знайдемо вираз для визначника другого порядку:

.

Оскільки можна скласти два різні добутки елементів визначника, що беруться по одному з кожного рядка і стовпця, то

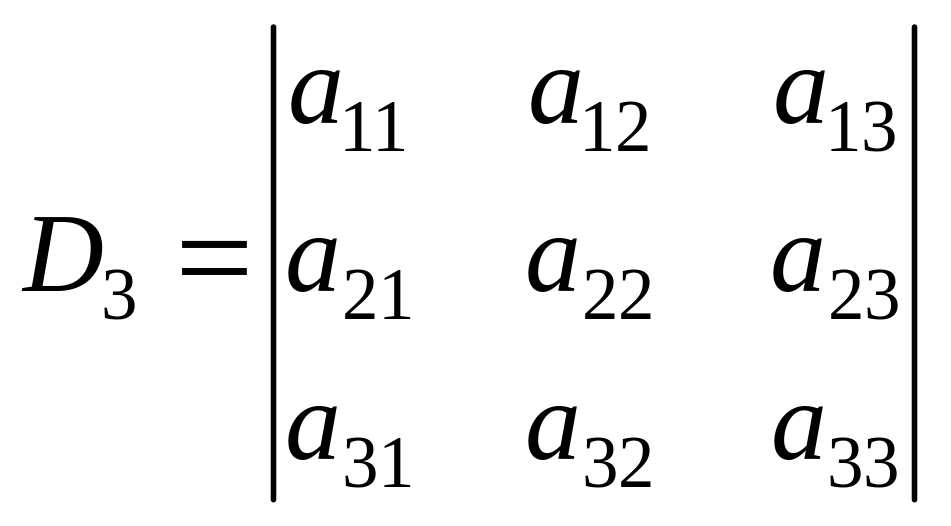. (2)

Усього існує 6 різних добутків елементів визначника, що беруться по одному з кожного рядка і кожного стовпця.

Згідно з (1) дістанемо вираз:

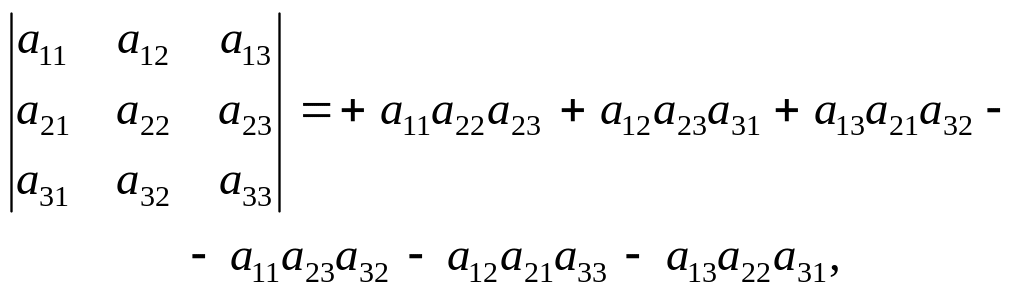
що являє собою визначник третього порядку.

Існує простий спосіб розкриття визначника третього порядку — так зване правило Саррюса. Допишемо до визначника (2) перший і другий стовпці, а далі перемножатимемо елементи, що розміщені на одній лінії, як показано на схемі:

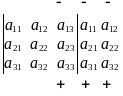
Добуток елементів, які розміщені на лініях, що йдуть згори ліворуч униз праворуч, береться зі знаком «+». Добуток елементів, розміщених на лініях, що йдуть згори праворуч униз ліворуч, береться зі знаком «–».

О бчислимо визначник третього порядку

.

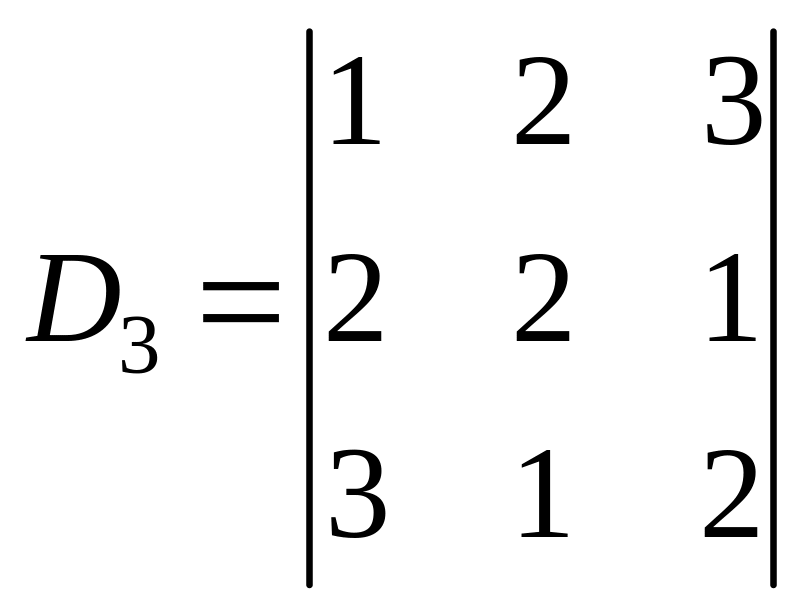 За правилом Саррюса складемо таблицю

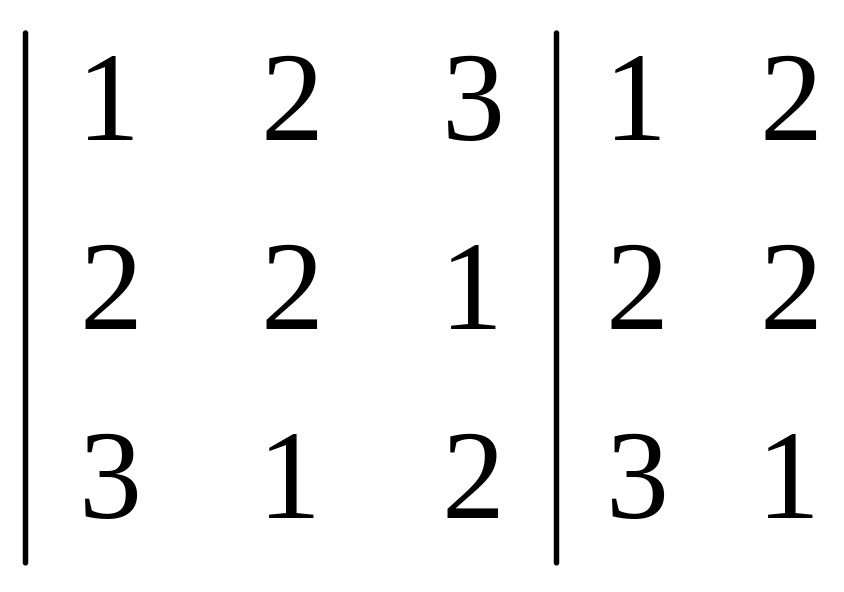
і знайдемо значення визначника:

D₃ = 1  2  2 + 2  1  3 + 3  2  1 – 3  2  3 – 1  1  1 – 2  2  2 = –11. 

Оскільки визначник n-го порядку складається з n! доданків, то формула (1) не застосовується для обчислення визначників при n > 3 (уже при n = 4 визначник містить 4! = 24 доданки).

Для обчислення визначників застосовують властивості, що розглядаються далі.