2.2.5. Подібні матриці

Означення. Матриці А і С називаються подібними між собою, якщо існує неособлива матриця В, така, що

С  = В^–1АВ, А = ВСВ^–1. (1)

Доведемо, що лінійне перетворення в різних базисах визначається подібними матрицями.

Нехай в n-вимірному лінійному просторі задано канонічний базис і довільний базис . Розглянемо лінійне перетворення простору у і розкладемо вектори за базисом :

.

Помноживши рівності

скалярно на вектор , дістанемо рівняння

. (2)

Перетворення (2) можна записати у вигляді

(3)

Візьмемо ще один базис і розкладемо за ним вектори :

. (4)

Нехай вектори у базисі подаються виразами

.

Тоді згідно з (4) маємо векторні рівності:

.

Лінійне перетворення (3) у новій системі координат набирає вигляду

. (5)

Здобутий результат доводить сформульовану далі теорему.

Теорема 1. Лінійне перетворення в різних базисах визначається подібними матрицями.

Р озглянемо множину векторів на площині.

Нехай лінійне перетворення полягає в повороті вектора на 90 проти годинникової стрілки. Розглянемо основні координатні вектори , що утворюють канонічний базис. При цьому маємо рівності , де А — матриця лінійного перетворення.

Отже, в канонічному базисі лінійне перетворення визначається матрицею

.

Візьмемо інший довільний базис, наприклад . При цьому маємо рівність (рис. 2.6).

Рис. 2.6

Розкладемо вектори за базисом :

Отже, лінійне перетворення в новому базисі визначається матрицею

.

Ця матриця буде подібною до матриці А. Справді:

.

2.2.6. Симетричні та несиметричні матриці

Розглядатимемо квадратні матриці n-го порядку. Нагадаємо, що матриця А називається симетричною, якщо А' = A, і кососиметричною, якщо А' = –A.

Теорема. Будь-яку квадратну матрицю А можна єдиним чином подати у вигляді суми симетричної та кососиметричної матриць.

Доведення. Запишемо симетричну матрицю А_s = 0,5 (A + A') та кососиметричну матрицю А_с = 0,5 (A – A'). Для них згідно з властивістю виконуються рівності:

= 0,5 (A' + A) = А_s, А_с' = 0,5 (A' – A) = –А_с .

Звідси маємо

А = А_s + А_с,

що й потрібно було довести.

П одамо матрицю А у вигляді суми симетричної та кососиметричної матриць:

2.2.7. Ортогональні матриці

Важливим для застосувань є лінійне перетворення , яке не змінює довжини вектора, тобто . Знайдемо скаляр­ні добутки:

.

Із порівняння найдених виразів випливає, що рівність

можлива лише за умови , де Е — одинична матриця.

Означення. Матриця А називається ортогональною, якщо .

Нехай стовпцями матриці А є вектори :

.

Знайдемо добуток матриць :

.

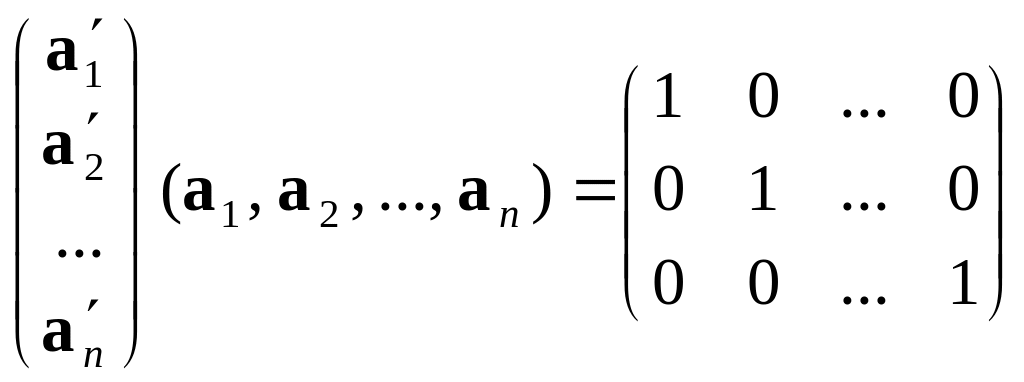Звідси маємо:

,

тобто стовпці матриці А утворюють ортонормовану систему векторів.

Далі застосовуватимемо символ Кронекера :

.

Для ортогональної матриці А можна записати:

.

Зауважимо, що для такої матриці А обернена матриця А^–1 збігається з транспонованою А.

Оскільки , тобто , то рядки ортогональної матриці утворюють ортонормовану систему векторів.

О ртогональною матрицею другого порядку є матриця

.

О ртогональна матриця третього порядку

має ортонормовані системи стовпців і рядків.

Для ортогональної матриці А з рівностей , випливає, що матриця також буде ортогональною.

Доведемо, що добуток ортогональних матриць А, В також є ортогональною матрицею.

 Справді, маємо рівність

,

яка й доводить ортогональність матриці АВ. 

З ауваження. Систему лінійних алгебраїчних рівнянь з n невідомими можна подати у вигляді

АХ = В. (1)

Якщо відома обернена матриця А^–1, то знаходимо розв’язки:

(2)

Коли в системі (1) матриця А ортогональна, розв’язки виду (2) можна подати так:

.