2.2.3. Існування розв’язків системи лінійних алгебраїчних рівнянь

Створено багато методів і способів розв’язування системи лінійних алгебраїчних рівнянь. Розглянемо найважливіші з них, що спираються на поняття рангу матриці.

Означення. Рангом матриці А називається ранг її векторів-стовпців.

Отже, рангом матриці можна назвати найбільше число лінійно незалежних її стовпців. Далі за допомогою теорії визначників буде доведено, що ранг матриці дорівнює також найбільшому числу лінійно незалежних її рядків. Із теореми 6, наведеної в підрозд. 2.1.3, випливає така теорема.

Теорема 1. Ранг матриці не змінюється в результаті еквівалентних перетворень стовпців або рядків матриці.

За допомогою еквівалентних перетворень досягають того, щоб якомога більше елементів матриці дорівнювали нулю. Для обчислення рангу матриці користуються наведеною далі теоремою.

Теорема 2. Нехай у матриці А в кожному рядку і кожному стовпці міститься не більш як один ненульовий елемент. Тоді дорівнює загальному числу всіх ненульових елементів матриці А.

Доведення теореми випливає з того, що стовпці матриці, які містять ненульові елементи, будуть лінійно незалежні. 

З найдемо ранг матриці

.

 Помножимо перший рядок на 2 і віднімемо від другого рядка. Далі помножимо перший рядок на 3 і віднімемо від третього рядка. У результаті дістанемо еквівалентну матрицю:

.

Віднявши другий рядок від третього, запишемо матрицю

.

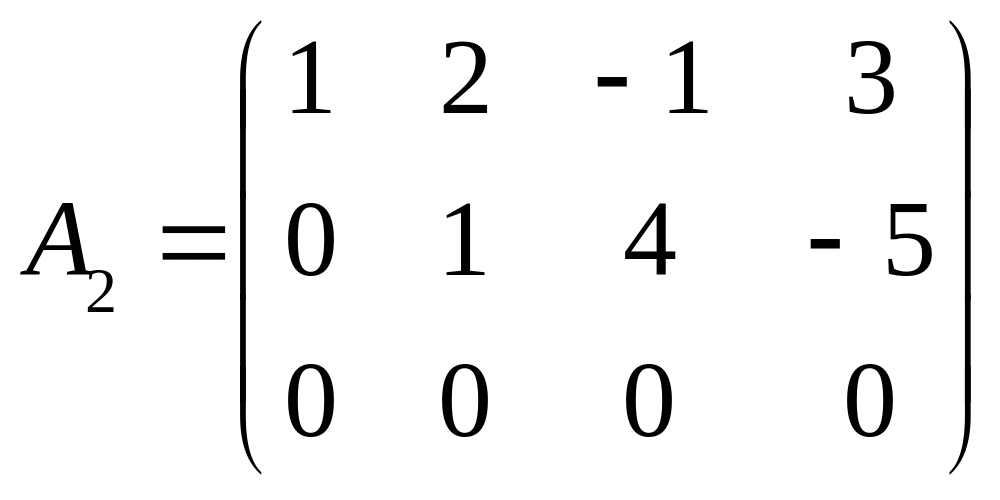Обчислення рангу матриці на цьому етапі можна припинити, оскільки матриця А₂ має лише два ненульові рядки. Звідси випливає, що ранг матриці А₂ не може бути більшим за два. Крім того, матриця А₂ має два ненульові лінійно незалежні рядки. Отже, .

Продовжимо еквівалентні перетворення матриці А₂. Помножимо перший стовпець на 2 і віднімемо від другого стовпця, далі додамо перший стовпець до третього, помножимо перший стовпець на 3 і віднімемо від четвертого стовпця. Зрештою дістанемо матрицю

.

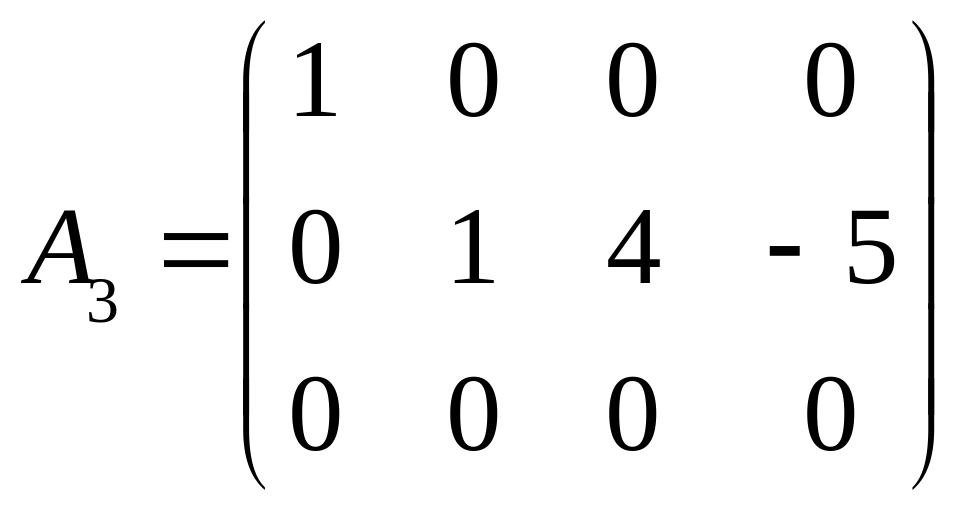Помножимо другий її стовпець на 4 і віднімемо від третього стовпця, далі помножимо другий стовпець на 5 і додамо до четвертого стовпця. У результаті утвориться матриця

,

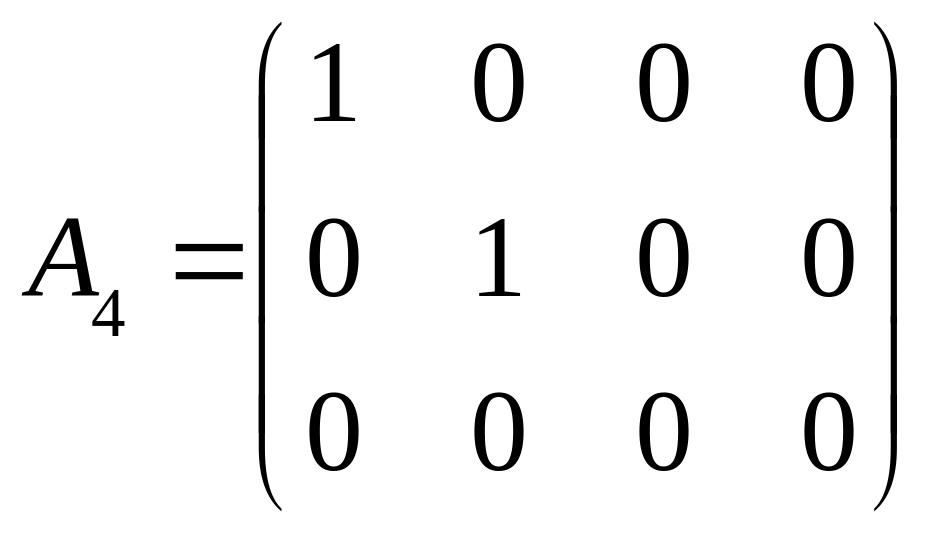яка в кожному рядку і кожному стовпці має не більш як один ненульовий елемент. Таким чином, .

Перейдемо до розгляду систем лінійних алгебраїчних рівнянь. Їх розв’язування зводиться до виконання еквівалентних (тобто таких, що не змінюють розв’язків) перетворень системи рівнянь. А саме, можна переставляти рівняння, множити рівняння на числа, відмінні від нуля, і додавати до одного рівняння інше, помножене на деяке число.

Означення. Якщо система лінійних рівнянь має розв’язки, то вона називається сумісною. Якщо система рівнянь не має роз­в’язків, то вона називається несумісною, або суперечливою. Якщо розв’язок системи єдиний, то система називається визначеною. Якщо система має більш як один розв’язок, її називають невизначеною.

Із теореми 4, наведеної в підрозд. 2.2.2, випливають розглянуті далі висновки щодо розв’язків однорідної системи лінійних алгебраїчних рівнянь виду

(1)

Теорема 3. Для того щоб однорідна система лінійних алгебраїчних рівнянь (1) мала єдиний нульовий розв’язок , необхідно і достатньо, щоб при дефект матриці

(2)

коефіцієнтів цієї системи дорівнював нулю.

Іншими словами, система лінійних однорідних рівнянь (1) має лише нульовий розв’язок, якщо ранг матриці А дорівнює n.

Теорема 4. Для того щоб однорідна система рівнянь (1) мала ненульовий розв’язок, необхідно і достатньо, щоб ранг матриці А був меншим від n.

Оскільки при ранг матриці А не може бути більшим за m, то при система однорідних рівнянь (1) є невизначеною і завжди має ненульовий розв’язок.

Теорема 5. Якщо ранг r матраці А менший за n, то загальне число лінійно незалежних ненульових розв’язків системи (1) дорівнює дефекту матриці: .

При цьому загальні розв’язки системи (1) можна подати у вигляді

,

де — лінійно незалежні розв’язки системи рівнянь .

Розглянемо тепер неоднорідну систему лінійних алгебраїчних рівнянь

(3)

Теорема 6. (Кронекера—Капеллі). Для того щоб неоднорідна система лінійних алгебраїчних рівнянь (3) була сумісною, необхідно і достатньо, щоб ранг матриці А виду (2) дорівнював рангу розширеної матриці

.

Доведення. Якщо , то перший стовпець матриці є лінійною комбінацією решти її стовпців, а отже, система рів­нянь (3) має розв’язки.

Коли система (3) має розв’язки, то перший стовпець матриці є лінійною комбінацією решти її стовпців. Звідси випливає, що матриці і містять однакове число лінійно незалежних стовпців. Отже, , що й доводить теорему. 

Загальний розв’язок системи рівнянь (3) складається з частинного розв’язку системи (3) та загального розв’язку однорідної системи (1). Таким чином, очевидними є наведені далі теореми.

Теорема 7. Для того щоб неоднорідна система рівнянь (3) мала єдиний розв’язок, необхідно, щоб .

Теорема 8. Нехай . Система неоднорідних рівнянь (3) має загальний розв’язок виду

,

де — частинний розв’язок неоднорідної системи рівнянь (3), а — лінійно незалежні розв’язки однорідної системи .

Можна дійти висновку, що коли число m рівнянь у системі (3) менше за число невідомих n, то ця система або невизначена, або суперечлива.

С истема рівнянь є несумісною.

 Справді, якщо перше рівняння помножимо на 2 і віднімемо від другого рівняння, дістанемо неможливу числову рівність 0 = 1. 