2.1.5. Обчислення рангу системи векторів

Обчислюючи ранг системи векторів, можна транспонувати вектори, тобто замінювати вектори-стовпці векторами-рядками. У результаті транспонування ранг системи векторів не змінюється.

Щоб обчислити ранг системи векторів, виокремлюємо в ній лінійно незалежні вектори (див. підрозд. 2.1.3). Наприклад, b₁ буде лінійно незалежним від інших векторів , якщо і-та координата вектора b₁, відмінна від нуля, а і-ті координати решти векторів дорівнюють нулю.

З огляду на сказане дістаємо такий метод виокремлення лінійно незалежних векторів.

1. У заданій системі векторів відшукуємо вектор, в якого перша координата відмінна від нуля. Якщо всі перші координати векторів дорівнюють нулю, то шукаємо вектор, в якого друга координата відмінна від нуля, і т. д. Нехай це буде вектор .

2. Множимо вектор на і віднімаємо від вектора так, щоб вибрана координата перетворилася на нуль.

3. Зі здобутих векторів знову виокремлюємо вектор, лінійно незалежний від інших векторів, способом, зазначеним у п. 1 і 2.

Кількість лінійно незалежних векторів дорівнює рангу системи векторів.

З найдемо ранг системи п’яти векторів у R⁷:

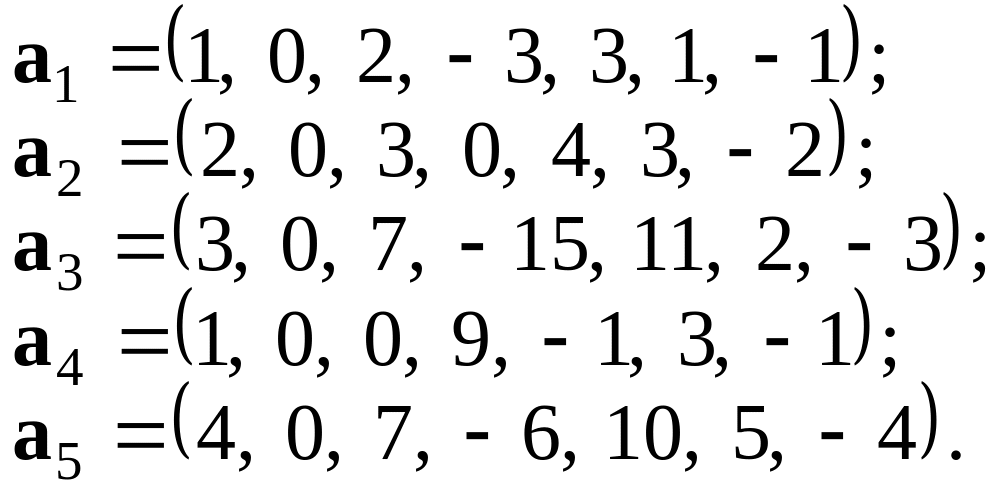(1)

Перша координата а₁ відмінна від нуля. Помножимо а₁ на 2 і віднімемо від а₂; помножимо вектор а₁ на 3 і віднімемо від а₃; далі віднімемо вектор а₁ від а₄, остаточно, помножимо вектор а₁ на 4 і віднімемо від вектора а₅. Дістанемо систему векторів:

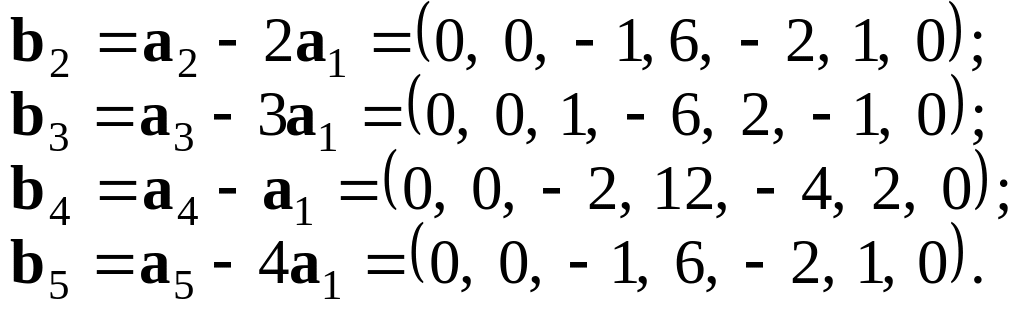
Оскільки другі координати всіх векторів дорівнюють нулю, то за другий лінійно незалежний вектор візьмемо b₂, в якого третя координата відмінна від нуля.

Запишемо вектори, в яких третя координата дорівнює нулю:

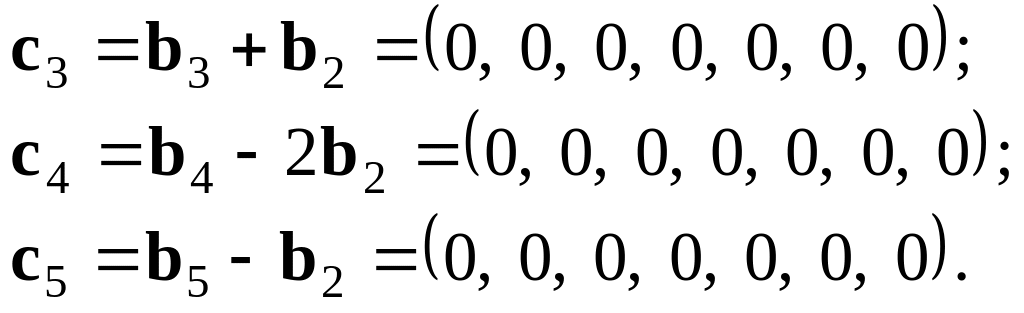
Оскільки всі вектори нульові, то вихідна система векторів містить лише два лінійно незалежні вектори, тобто ранг цієї системи дорівнює двом.

Другий спосіб обчислення рангу системи векторів полягає в ортогоналізації векторів.

Утворюється послідовність ортонормованих векторів:

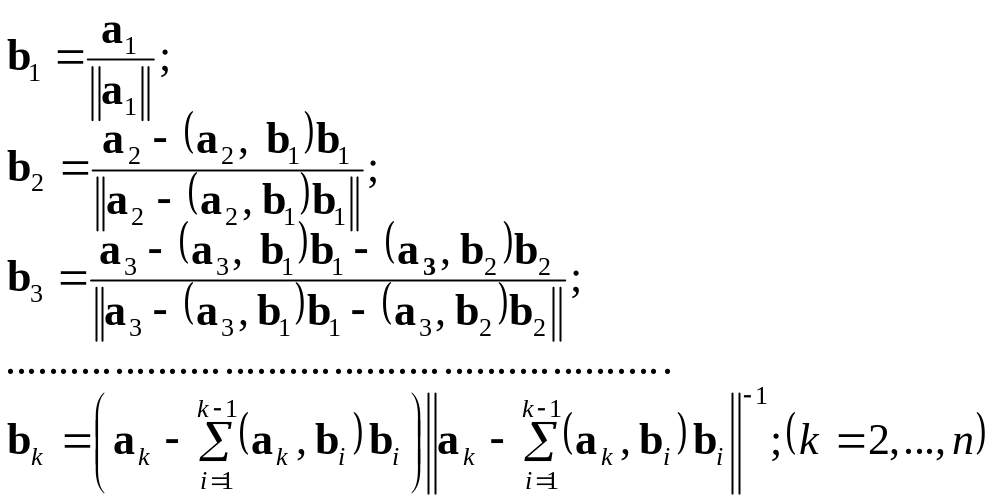(2)

Якщо при деякому значенні k

,

то вважаємо . У такому разі вектор є лінійною комбінацією векторів Кількість ненульових векторів у системі дорівнює рангу цієї системи.

Р озглянемо систему векторів (1) і знайдемо

;

.

Знайдемо скалярний добуток векторів і , розглядаючи перший як вектор-рядок, а другий — як вектор-стовпець:

а також виконаємо обчислення згідно з виразом із (2) для вектора :

Звідси

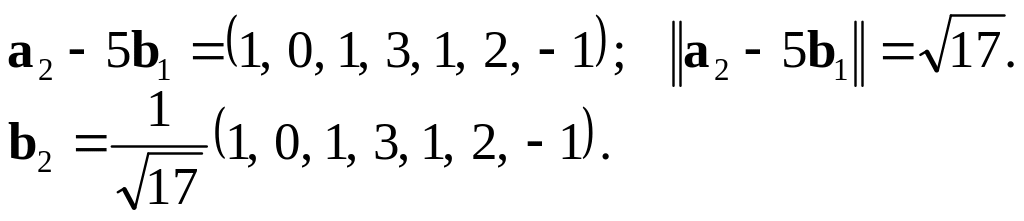
Далі, розглядаючи як вектор-рядок, а і як вектори-стовпці, дістаємо:

;

.

Знаходимо вектор

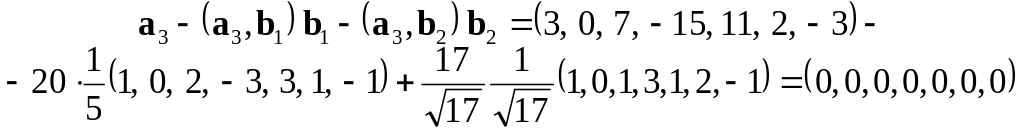
і, як наслідок, вважаємо .

Аналогічно згідно з (2) відшукуємо вектори

Зауважимо, що розглянутий приклад є суто навчальним. У реальних завданнях координати векторів дістають наближеними обчисленнями. Тому лінійно залежні або незалежні вектори будуть лише наближено лінійно залежні або незалежні. Можна запропонувати такий наближений алгоритм, що легко реалізується на ЕОМ.

1. Беруть достатньо мале число , .

2. Обчислюють послідовно вектори за формулами (2). Якщо , то вважають ; якщо , то беруть ; якщо

,

то покладають .

3. Кількість ненульових векторів у системі наближено дорівнює рангу системи векторів .

* Транспонування вектора є частинним випадком транспонування матриці (див. підрозд. 2.2.1), причому вектор-стовпець являє собою матрицю розміру п  1 (п — кількість рядків), а вектор-рядок — матрицю розміру 1  п (п — кількість стовпців).

* Це випливає з правила множення матриць (див. підрозд. 2.2.4).

84