2.1.4. Лінійні комбінації векторів. Ранг системи векторів

Означення. Вектор називається лінійною комбінацією векторів , якщо існують сталі числа такі, що справджується рівність

. (1)

Якщо подати через координати

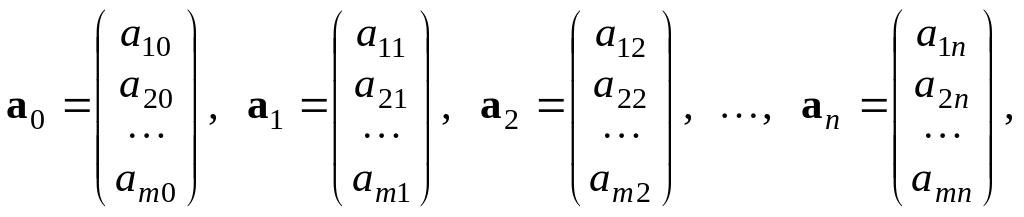
то векторна рівність (1) буде рівносильна системі лінійних алгебраїчних рівнянь:

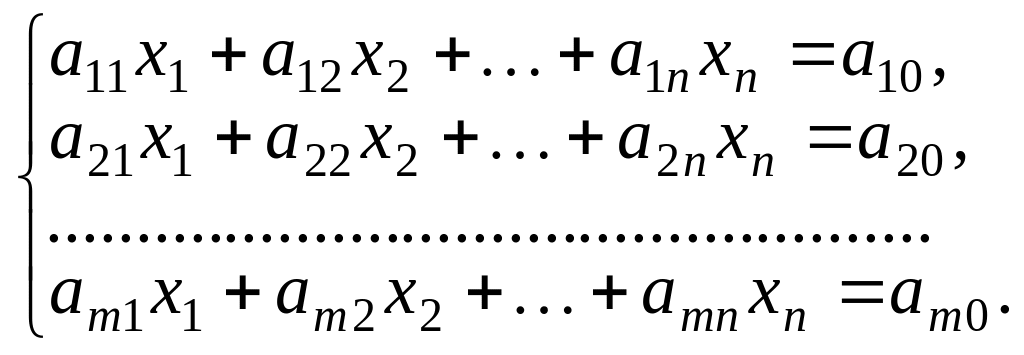(2)

Очевидно, що виконується сформульована далі теорема.

Теорема 1. Для того, щоб система лінійних алгебраїчних рівнянь (2) була сумісною, тобто мала розв’язки, необхідно і достатньо, щоб вектор був лінійною комбінацією векторів .

Лінійна залежність і незалежність системи векторів пов’язана з поняттям лінійної комбінації векторів.

Теорема 2. Для того, щоб вектори були лінійно залежними, необхідно і достатньо, щоб один із цих векторів був лінійною комбінацією решти.

Доведення. Нехай вектори лінійно залежні. Це означає, що рівність

виконується, коли коефіцієнти одночасно не перетворюються на нуль. Не втрачаючи загальності міркувань, можна вважати, що . Тоді

,

тобто вектор є лінійною комбінацією векторів .

Доведемо обернене твердження. Припустимо, що в системі один із векторів, наприклад , є лінійною комбінацією решти векторів:

.

Тоді виконується рівність

,

з якої за означенням випливає, що вектори — лінійно залежні.

Зауважимо, що два вектори , будуть лінійно залежними, якщо в них пропорційні всі координати, тобто .

Означення. Нехай V — непорожня підмножина векторів із . V називається лінійним підпростором у , коли з умов , випливає, що при , вектор

Візьмемо систему векторів , що належать Множина всіх лінійних комбінацій цих векторів

, , (3)

утворює лінійний підпростір V у .

Справді, якщо , , , , то виконується рівність

,

тобто .

Підпростір V, утворений лінійними комбінаціями виду (3), називається лінійною оболонкою системи векторів , або підпростором, породженим векторами .

Означення. Найбільше число r лінійно незалежних векторів у системі векторів називається її рангом і позначається

.

Якщо ранг системи n векторів дорівнює r (r < n), то будь-які (r + 1) векторів цієї системи лінійно залежні. Число d = n – r називається дефектом системи векторів.

Означення. Нехай V — підпростір у . Система векторів називається базисом у V, якщо вона лінійно незалежна і її лінійна оболонка збігається з усім простором V.

Доведемо тепер сформульовану далі теорему.

Теорема 3. Якщо система векторів утворює базис підпростору V, то кожний вектор подається єдиним чином у вигляді лінійної комбінації векторів :

. (4)

Доведення. Припустимо, що векторний підпростір V породжено векторами із , а система векторів має ранг r і базис . Якщо , то будь-який вектор з V подається у вигляді лінійної комбінації векторів :

. (5)

Беручи до уваги (4) і (5), доходимо висновку, що справджується рівність

. (6)

Оскільки вектори — лінійно незалежні, то згідно з (6) . Отже, подання вектора у вигляді лінійної комбінації (4) єдине.

Якщо , то система векторів , лінійно залежна, тобто рівність

(7)

можлива, коли коефіцієнти , одночасно не перетворюються на нуль. При цьому , оскільки при з лінійної незалежності векторів випливає, що . Згідно із (7) дістаємо подання вектора

у вигляді лінійної комбінації векторів базису .

Таким чином, будь-який вектор , що є лінійною комбінацією векторів , а саме:

можна подати через базисні вектори , тобто у вигляді (4):

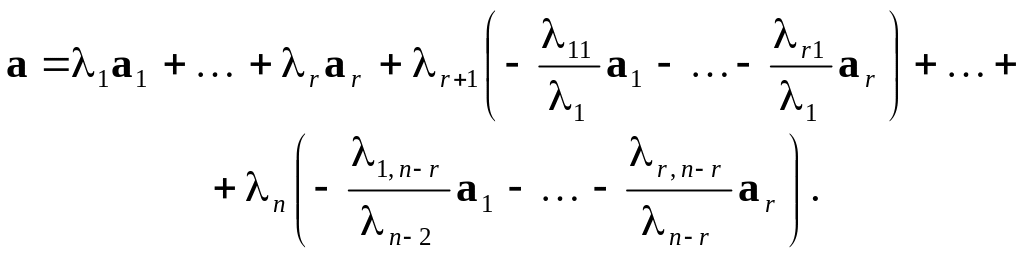
Єдиність подання (4) доведено раніше.

Доведемо, що ранг системи векторів не залежить від вибору множини лінійно незалежних векторів. Спочатку розглянемо доведення теореми Стейніца.

Теорема 4. Якщо — лінійно незалежні вектори з підпростору , базис якого , тоді k векторів базису можна замінити на вектори .

Доведення. Подамо вектор через вектори базису

.

Оскільки , то принаймні один із коефіцієнтів відмінний від нуля. Не поступаючись загальністю міркувань, мож­на вважати, що . При цьому знаходимо вектор , виражений через :

.

Звідси випливає, що вектори утворюють базис у підпросторі V.

Розглянемо вектор , який можна подати лінійною комбінацією векторів :

.

Хоча б один із коефіцієнтів відмінний від нуля, оскільки при дістаємо хибну рівність .

Не поступаючись загальністю міркувань, вважаємо, що . Отже, вектор можна подати через вектори :

.

Звідси випливає, що утворюють базис.

Повторюючи наведені дії k разів, дістаємо базис підпростору V. Отже, теорему доведено.

Наслідок. Нехай маємо два базиси підпростору V: і . Із доведення теореми випливає, що множина векторів не може бути базисом підпростору V, оскільки при цьому вектор можна подати лінійною комбінацією векторів . Звідси маємо, що вектори , не утворюють базису підпростору V.

Оскільки нерівності , неможливі, то .

Здобутий висновок сформулюємо у вигляді теореми.

Теорема 5. Якщо ранг векторів дорівнює r , то базис підпростору , породженого век­торами , завжди являє собою систему r лінійно незалежних векторів.

Означення. Якщо векторний простір V має базис , то всі базиси цього простору V складаються з r лінійно незалежних векторів. Це число називають розмірністю простору V і позначають . Будь-які r лінійно незалежних векторів із простору V утворюють його базис.

Р озглянемо підпростір V, породжений лінійною комбінацією векторів із :

Оскільки , , то підпростір V має базис, що складається з двох лінійно незалежних векторів , . Отже, .

Зауважимо, що в m-вимірному просторі R^m існує канонічний ортонормований базис

який складається з m векторів. Отже, будь-який базис підпростору V у просторі R^m не може містити більш ніж m векторів. Тому ранг системи векторів із R^m не може бути більшим за m.