2.1. Лінійний простір

2.1.1. Векторний простір

Означення. Упорядкована сукупність m дійсних чисел а₁, а₂, …, а_m називається m-вимірним вектором і позначається вектором-стовпцем або вектором-рядком:

.

Числа а₁ , а₂ , …, а_m називаються координатами, або проекціями, вектора а. Число m називається розмірністю вектора а. Перехід від запису вектора у вигляді стовпця до запису у вигляді рядка та навпаки називається транспонуванням вектора^*.

Вектор, утворений транспонуванням вектора а, позначається так: .

Означення. Два вектори називаються рівними, якщо рівні між собою їх відповідні координати.

Означення. Множина всіх m-вимірних векторів називається m-вимірним простором і позначається R^m.

Векторні простори R¹, R², R³ можна розглядати відповідно як множину векторів на прямій (множину дійсних чисел), множину векторів на площині та множину векторів у тривимірному просторі. На відміну від векторів числа називають скалярами.

Означення. Вектор називається нульовим, або нуль-вектором, якщо всі його координати дорівнюють нулю. Нульовий вектор позначається , або так само, як число нуль — знаком 0. Вектор називається протилежним вектору

На прямій , площині та у тривимірному просторі вектори можна геометрично зображати напрямленими відрізками. При цьому вони мають початок і кінець. Два вектори а, b є рівними між собою, якщо вони паралельні, мають одну й ту саму довжину та однаковий напрям. Рівні вектори можуть мати довільні різні початки. Сумі a + b векторів a та b відповідає діагональ паралелограма, побудованого на векторах a та b (рис. 2.1).

Рис. 2.1

Щоб дістати різницю векторів b – a, будуємо трикутник, зі сторонами, що їх утворюють ці вектори. Тоді вектор, початок якого збігається з кінцем вектора а, а кінець — із кінцем вектора b, являтиме собою шукану різницю. При цьому виконується рівність b – a = b + (–a) (рис. 2.2).

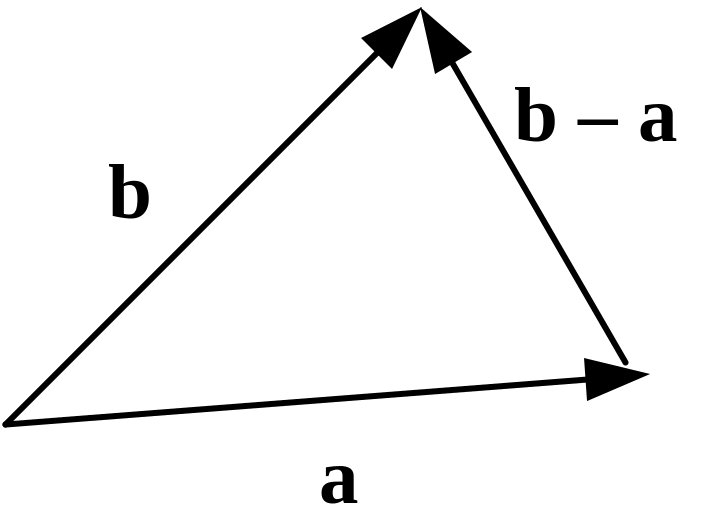
Рис. 2.2

Вектор a, де  — деяке число, паралельний вектору a і має довжину a; напрям його при той самий, що й вектора a, при — протилежний напряму a (рис. 2.3).

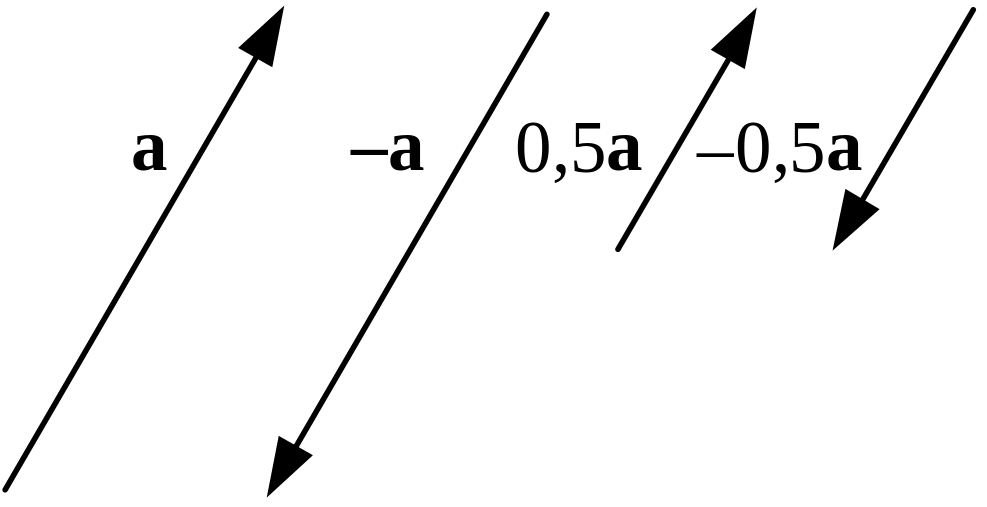
Рис. 2.3

Означення. Сумою двох векторів a та b називається вектор a + b, координати якого дорівнюють сумі відповідних координат векторів-доданків:

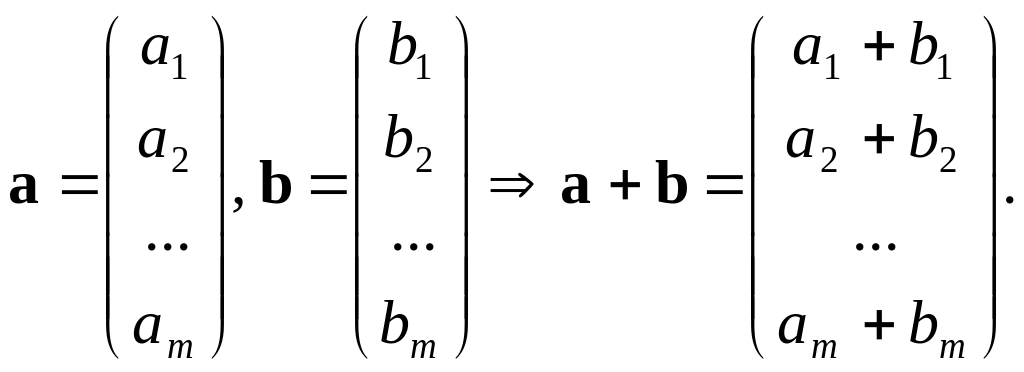
Добутком числа  (скляра) на вектор a називається вектор , координати якого дорівнюють добутку  на відповідні координати вектора a:

.

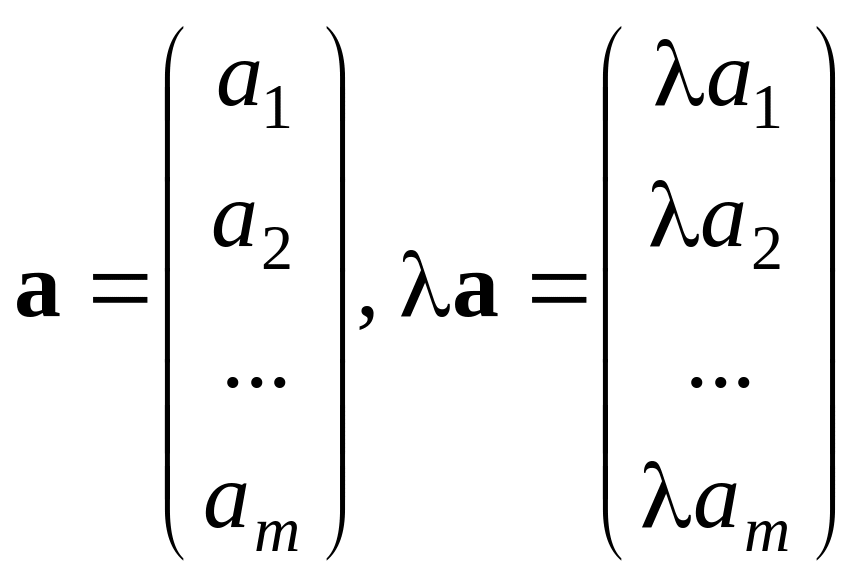Вектори a та b називаються колінеарними (паралельними), якщо їх відповідні координати пропорційні:

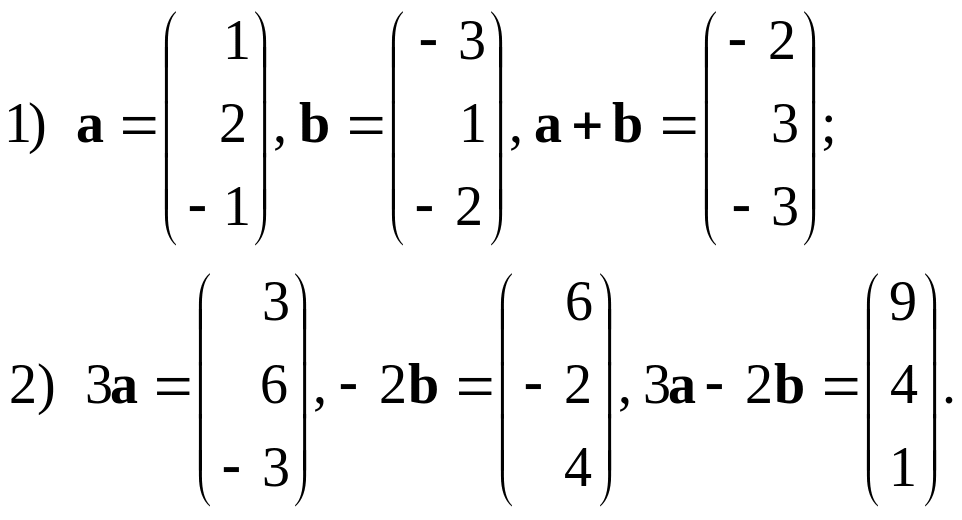
Властивості додавання векторів та множення числа на вектор (  — деякі числа):

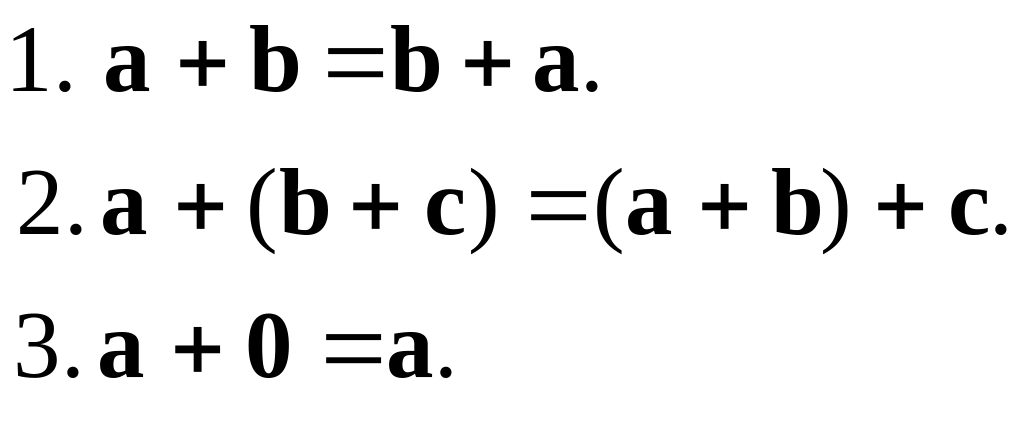
4. Для будь-якого вектора а існує протилежний вектор –а, такий що

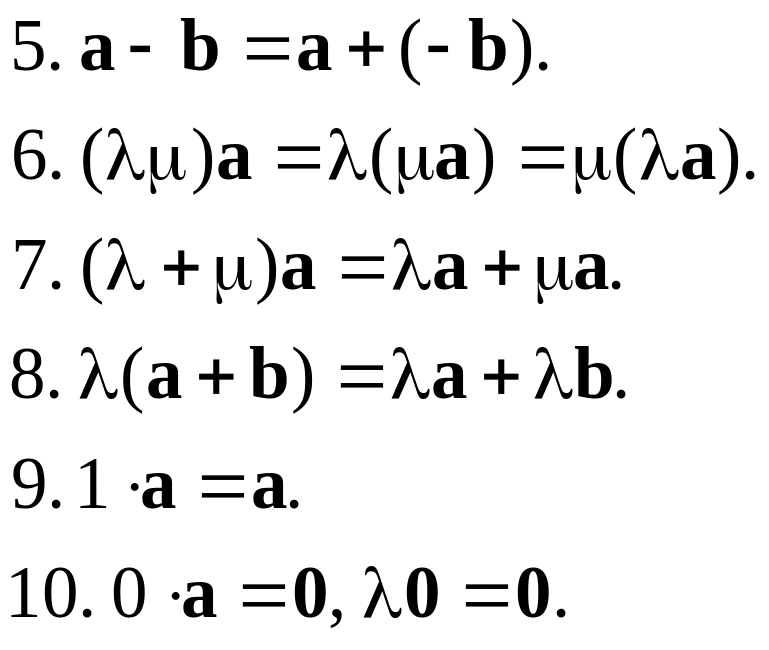
Означення. Скалярним добутком двох векторів

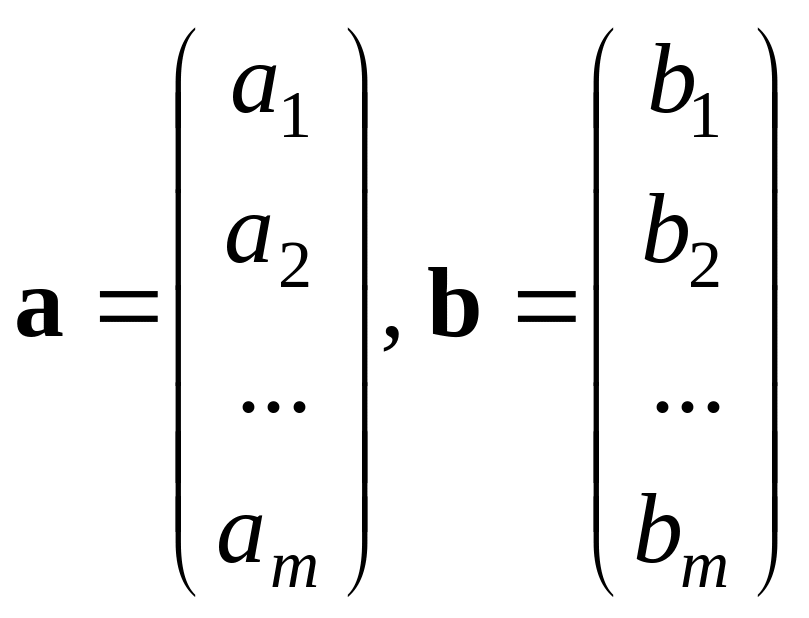
називається число, що визначається сумою попарних добутків відповідних координат:

.

Скалярний добуток можна подати також як добуток вектора-рядка на вектор-стовпець^*:

.

.

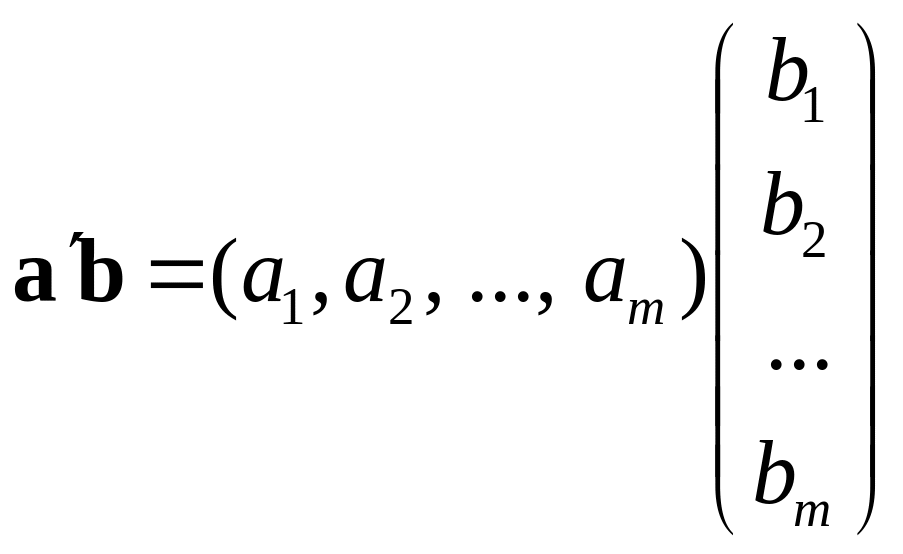
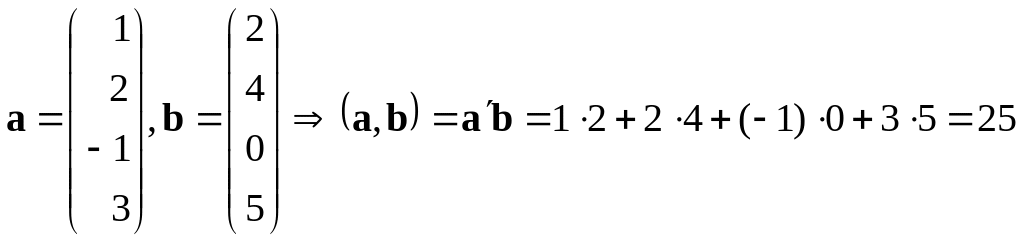Із означення скалярного добутку випливають такі його властивості:

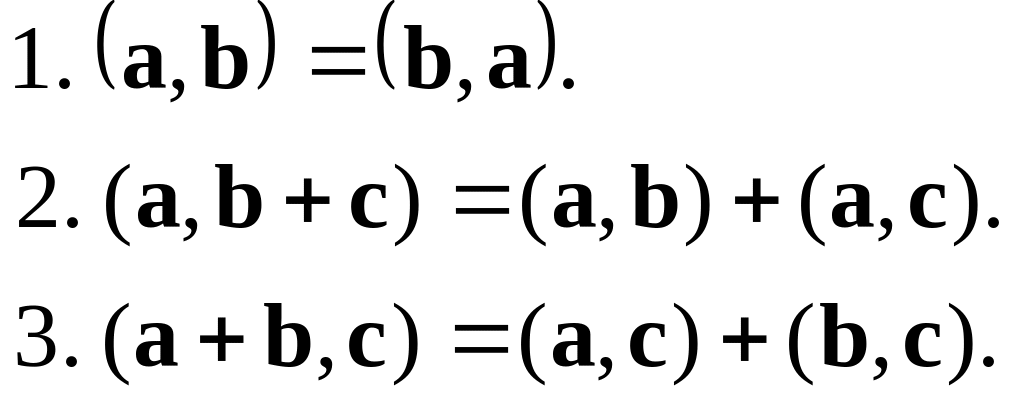
Означення. Два вектори, скалярний добуток яких дорівнює нулю, називаються взаємно ортогональними.

Нульовий вектор ортогональний до будь-якого вектора.

Якщо n векторів а₁, а₂,…,а_п попарно ортогональні між собою, то говорять, що ці вектори утворюють ортогональну систему.

Якщо два вектори ортогональні, то звідси не випливає, що один із них нульовий.

Н ехай дано вектори

.

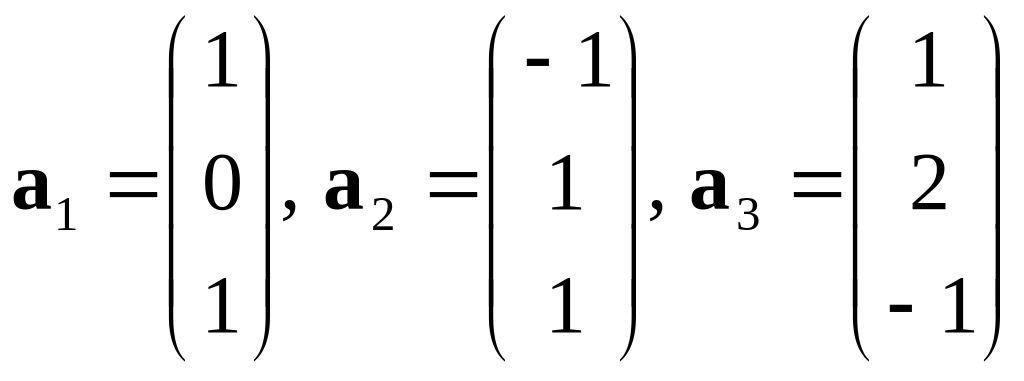Легко перевірити, що вони попарно ортогональні, але жодний із них не є нульовим. Вектори утворюють ортогональну систему у просторі R³.

Н ехай . Знайти таке число , щоб вектори та були взаємно ортогональними.

 Обчислимо скалярний добуток векторів :

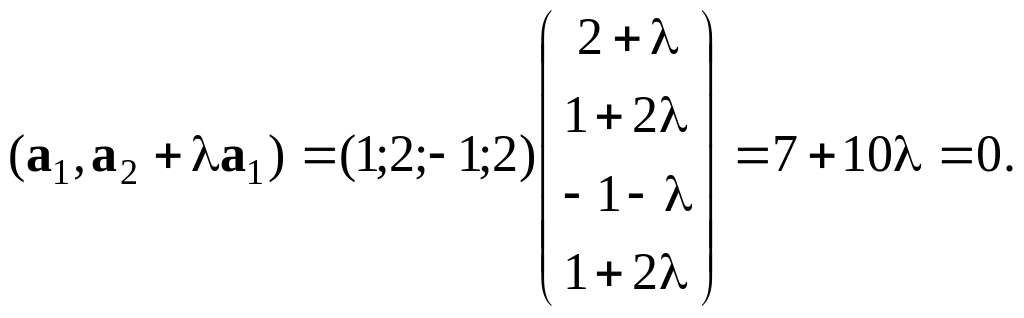
Звідси  = –0,7. Вектори будуть взаємно ортогональними.

З ауваження. Скалярному добутку можна дати економічну інтерпретацію, розглянувши m різних товарів відповідно кіль­кістю та ціною за одиницю товару. Загальну вартість усіх товарів можна подати скалярним добутком вектора кількості товарів і вектора цін :