Дифференциальные уравнения. Дифференциальные уравнения I порядка.

Понятие о дифференциальном уравнении.

Теория дифференциальных уравнений широко используется в естествознании и технике. В частности, при решении многих физических задач приходится находить неизвестную функцию по данному соотношению между неизвестной функцией, ее производными и независимыми переменными.

С формальной точки зрения задача решения дифференциального уравнения есть задача, обратная дифференцированию. Однако в теории дифференциальных уравнений приходится не только интегрировать заданное дифференциальное уравнение для отыскания искомой функции, но и зачастую по условию той или иной задачи составлять это уравнение и затем решать его.

Дифференциальным называют такое уравнение, в котором неизвестной является функция одной или нескольких переменных, причем в уравнение входит не только сама функция, но и ее производные.

Если неизвестная функция является функцией одной независимой переменной, то уравнение называется обыкновенным дифференциальным, если же – функцией нескольких переменных, то – дифференциальным уравнением в частных производных.

Порядок наивысшей производной (или дифференциала), входящей в дифференциальное уравнение, называется порядком уравнения.

В общем виде обыкновенное дифференциальное уравнение -го порядка можно записать так:

.

Например, есть дифференциальное уравнение второго порядка.

Любая функция, удовлетворяющая дифференциальному уравнению, называется решением или интегралом этого уравнения.

Решение дифференциального уравнения (если оно существует), в котором число произвольных постоянных равно порядку уравнения, называется общим решением данного дифференциального уравнения.

Общее решение обыкновенного дифференциального уравнения -го порядка записывается так:

.

Решения дифференциального уравнения при определенных значениях произвольных постоянных называется частным решением. Условия, которым должно удовлетворять искомое частное решение данного дифференциального уравнения, называются начальными условиями. Задача отыскания конкретного частного решения данного дифференциального уравнения по начальным данным называется задачей Коши.

Так как каждое частное решение данного дифференциального уравнения есть некоторая функция одной переменной, то в прямоугольной системе координат на плоскости этому решению соответствует некоторая линия. Она называется интегральной кривой данного дифференциального уравнения. Общему же решению дифференциального уравнения соответствует множество всех интегральных кривых этого уравнения, которое называется семейством интегральных кривых дифференциального уравнения.

Дифференциальным уравнением первого порядка называется уравнение вида: или . Его общее решение содержит одну произвольную постоянную С: .

Дифференциальные уравнения первого порядка иногда удобно записывать и в виде:

.

Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения.

Если функции и разлагаются на множители: , а , тогда уравнение вида:

называется уравнением с разделяющимися переменными.

Предположив, что , и разделив обе части первого уравнения на , получим уравнение с разделенными переменными:

,

которое интегрируется:

.

Вычисление полученных интегралов и дает общее решение уравнения с разделяющимися переменными.

Функция называется однородной функцией измерения ( ) относительно аргументов х и у, если равенство справедливо для любого , при котором функция определена.

Если , то функция будет однородной нулевого измерения .

Дифференциальное уравнение первого порядка называется однородным, если и - однородные функции от х и у одинакового измерения, т.е. Действительно, переписав его в виде: легко заключаем, что - однородная функция нулевого измерения, поскольку:

Так как однородное дифференциальное уравнение первого порядка всегда можно записать в виде то, положив , получим:

Данное уравнение решается с помощью замены и сводится к уравнению с разделяющимися переменными относительно х и новой функции :

. Отсюда следует: . Разделив переменные и выполнив почленное интегрирование, находят общее решение однородного дифференциального уравнения первого порядка.

Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли.

Дифференциальное уравнение первого порядка:

называется линейным, если оно линейно относительно неизвестной функции у и ее производной , где и - непрерывные функции от х.

Линейное дифференциальное уравнение первого порядка называется однородным, если , в противном случае оно неоднородное.

Линейное дифференциальное уравнение можно проинтегрировать методом Бернулли, суть которого заключается в следующем. Представим искомую функцию в виде произведения двух неизвестных функций и по формуле (подстановка Бернулли). Тогда Подставив выражения для у и у’ в линейное дифференциальное уравнение, получим:

,

которое преобразуем к виду:

.

Так как , то интегрирование данного вида уравнения сводится к интегрированию двух уравнений с разделяющимися переменными:

и

Найдя общее решение из первого уравнения, а затем и из второго уравнения, придем к общему решению линейного уравнения: .

Дифференциальное уравнение

где , называется уравнением Бернулли.

Путем введения новой функции по формуле , откуда , уравнение Бернулли сводится к линейному уравнению относительно этой функции:

Уравнение Бернулли, как и линейное уравнение можно решить с помощью подстановки Бернулли

Лекции 10-12.

Ряды. Числовые ряды.

Числовым рядом называется выражение , где - члены ряда, действительные или комплексные числа, - общий член ряда. Сумма n первых членов ряда называется n – ой частичной суммой ряда . Если предел при n существует и конечен, то ряд называется сходящимся: , где - сумма ряда. Разность между рядом и , называется остатком ряда .

Основными вопросами теории рядов являются:

1. Определить сходится или расходится ряд.

2. Найти сумму, если он сходится.

Исследовать на сходимость ряды (по определению):

1. геометрическая прогрессия ;

2. ;

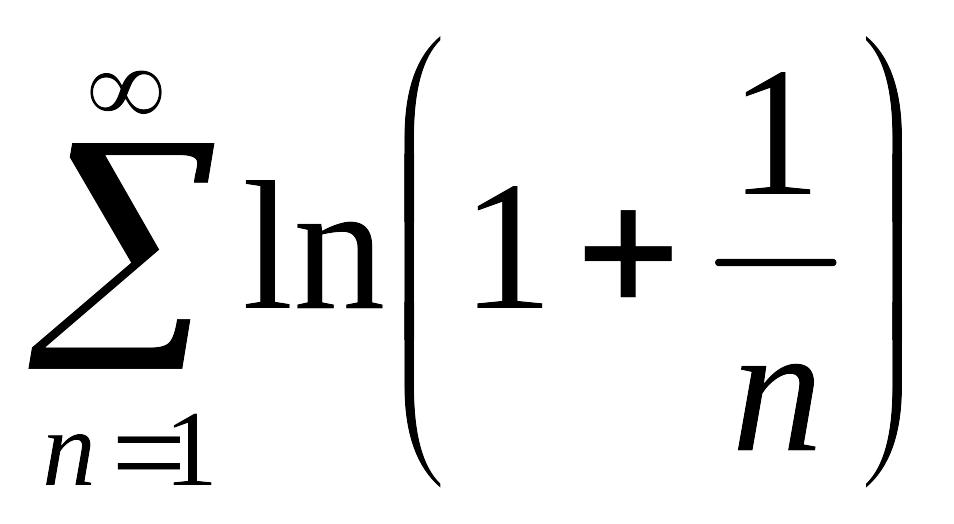3. гармонический ряд.

Рассмотрим свойства сходящихся рядов:

1. Если ряд 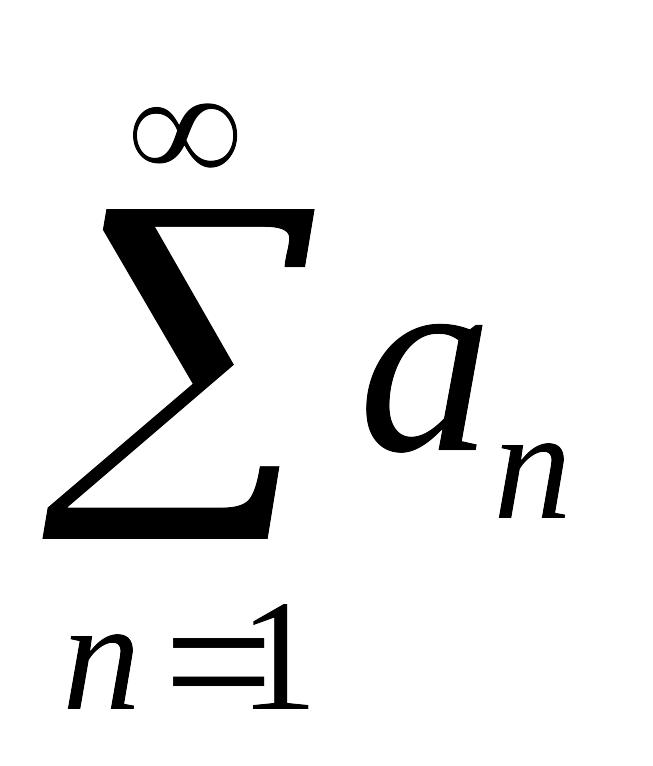сходится, то сходится ряд 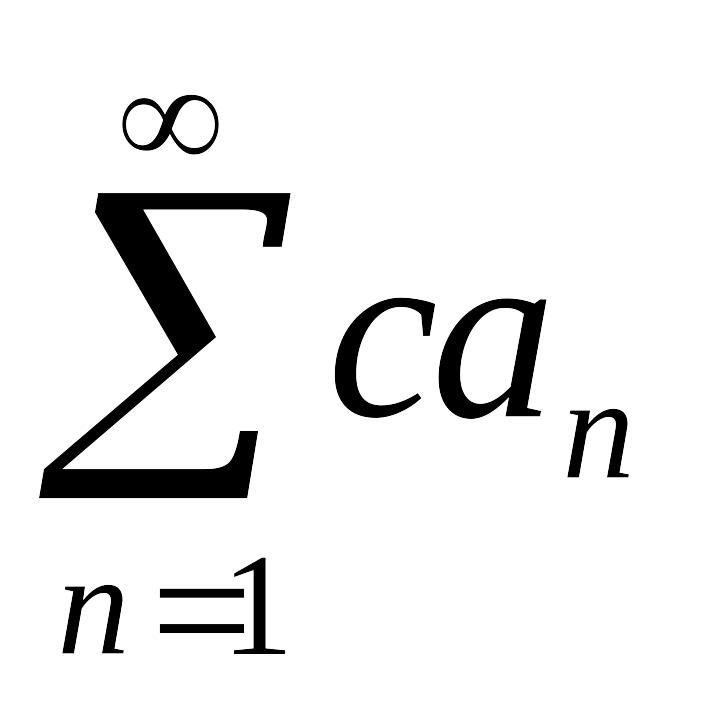, где с – постоянная.

2. Если ряд сходится и его сумма равна и сходится и его сумма равна , то ряд 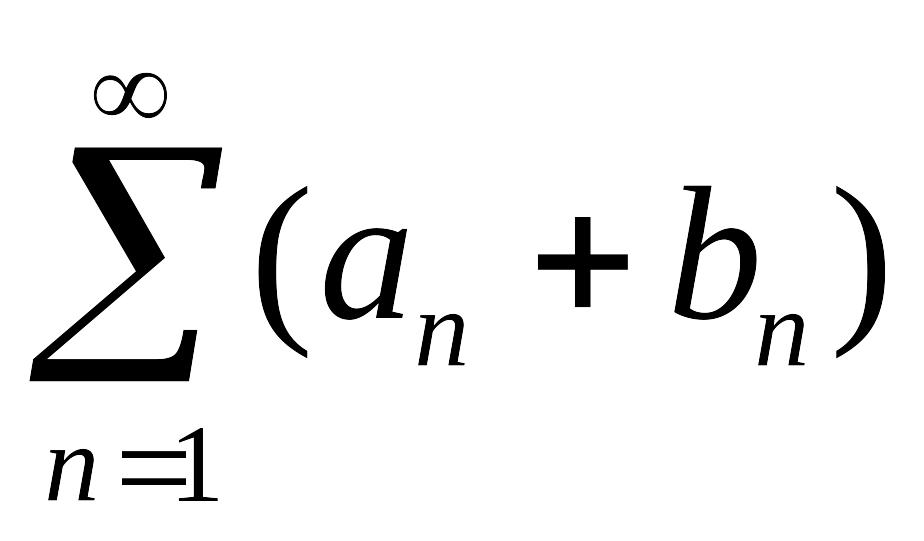сходится и его сумма равна + .

3. Если ряд сходится, то сходится ряд полученный из данного путем прибавления или отбрасывания конечного числа его членов.

4. Если ряд сходится, то 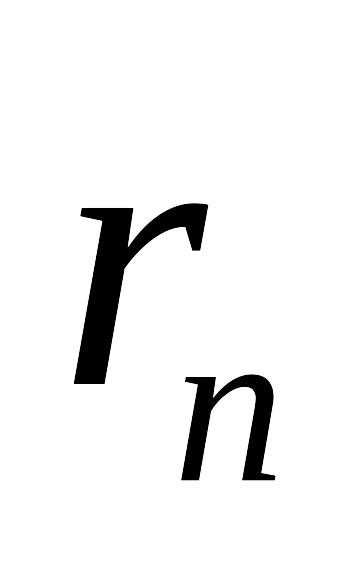- б.м. при .

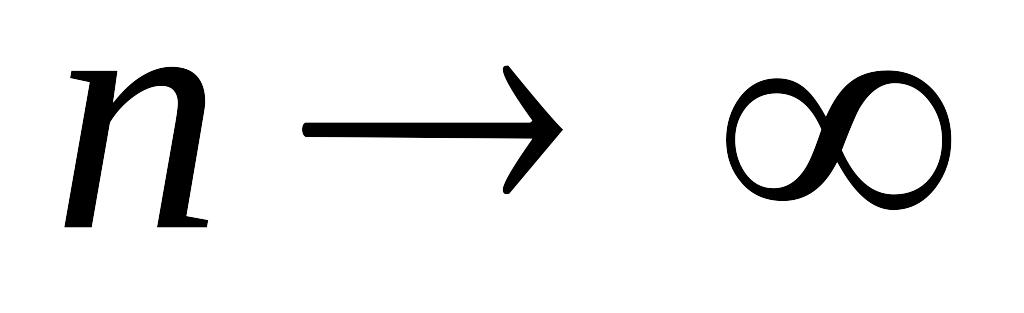5. Если ряд сходится, то .

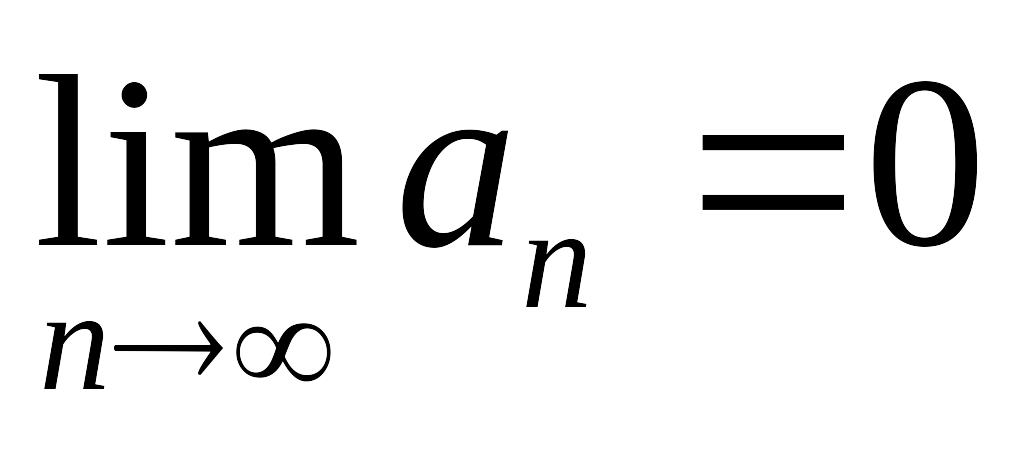6. Знакоположительные ряды. Общий принцип сходимости. Рассмотрим ряд , 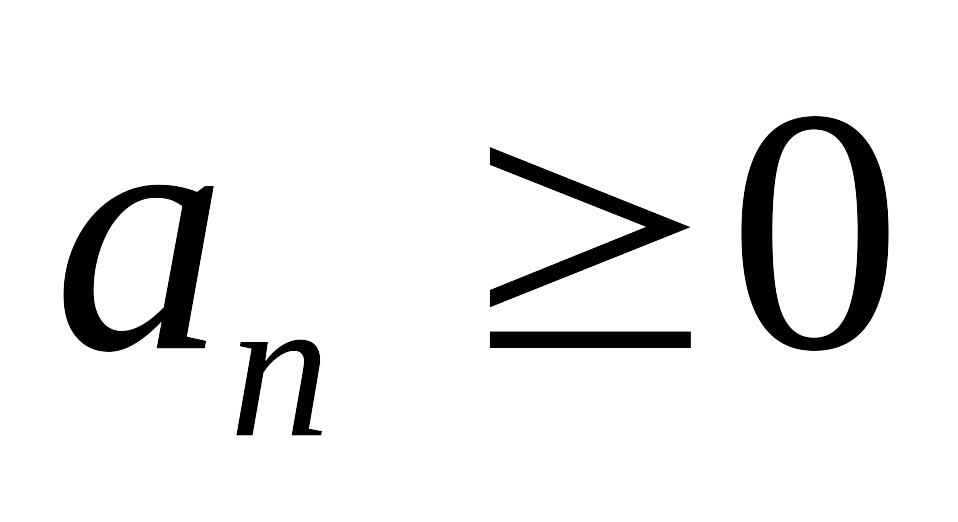для любого n и последовательность {S_n}. Очевидно, что {S_n} – возрастающая. Если эта последовательность ограничена, т.е. существует М для которого S_n<М, то по признаку Вейерштрасса {S_n} имеет предел, т.е. ряд сходится (критерий Коши); т.о., сходится, если S_n<М и наоборот.

7. Сформулировать достаточные признаки сходимости (два признака сравнения, признак Даламбера, радикальный и интегральный признак Коши).

Знакочередующиеся и знакопеременные ряды.

1. Знакочередующиеся ряды. Признак Лейбница.

2. Общий достаточный признак сходимости знакопеременных рядов.

3. Абсолютная и условная сходимость числовых рядов. Свойства абсолютно сходящихся рядов.

Знакочередующимся рядом называется ряд вида: .

Для знакочередующихся рядов имеет место достаточный признак сходимости (признак Лейбница): знакочередующийся ряд (1) сходится, если:

1. последовательность абсолютных величин членов ряда монотонно убывает, т.е. a₁>a₂>…>a_n>…;

2. .

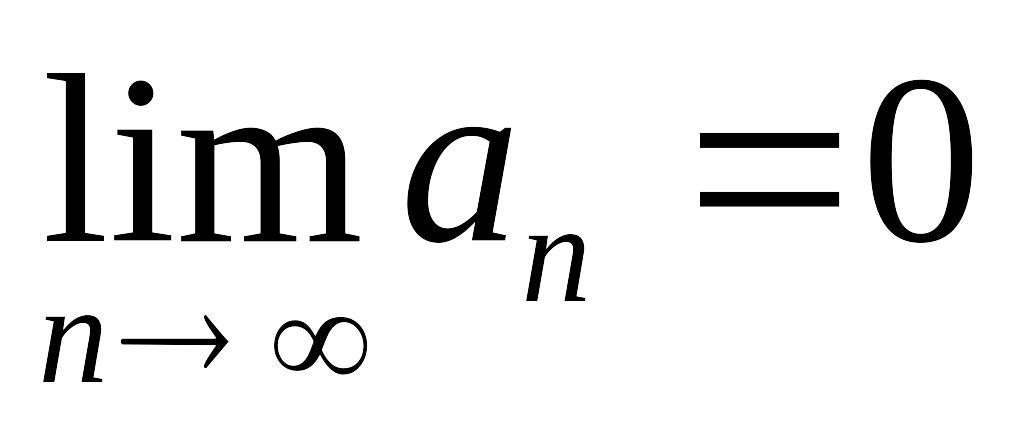При этом сумма S ряда удовлетворяет неравенствам 0<S<a₁. Последнее неравенство позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой S_n. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд , сумма которого, по модулю меньше первого члена этого ряда, т.е. S_n<a_n+1.

Пример. Вычислить сумму .

Взяв . Получим ошибку .

Ряд , содержащий бесконечное множество положительных и отрицательных членов, где нет строгого чередования знаков, называется знакопеременным.

Общий достаточный признак сходимости знакопеременных рядов: пусть дан знакопеременный ряд , если сходится ряд (2) , составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (1).

Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.

Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Основные свойства абсолютно сходящихся рядов приводятся без доказательства:

1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (Т. Дирихле).

2. Абсолютно сходящиеся ряды с суммами S₁ и S₂ можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна S₁ + S₂ (или S₁ - S₂).

В случае условно сходящихся рядов соответствующие утверждения (свойства), вообще говоря, не имеют места.

Пример. .

Переставим члены ряда местами:

.

Сумма уменьшилась вдвое.

Лекции 13-15.