3.4. Cовместный разряд ионов целевого металла и примесей

В этом случае на катоде совместно восстанавливаются ионы целевого металла и примесных элементов по схеме, изложенной в разделе 3.1. Рассмотрим его на примере 2-х реакций:

1) Mecn+ + nме ®Mec Jм

2) Kni+ + nie ®Mei Ji

где K – примесь, Me_c – целевой металл.

Основной задачей теории является выявление связи между содержанием примеси в металле и параметрами электролиза.

Обозначив через А массовую долю примеси в катодном металле, и используя закон Фарадея, можно записать:

A (3.11)

где q_i и q_м – электрохимические эквиваленты примеси и целевого металла.

Выражение (3.11) не отличается от выражения 3.6 (п 3.1), определяющего распределение тока между реакциями. Следовательно, и в этом случае, можно воспользоваться результатами анализа распределения тока между двумя реакциями, изложенными в п. 3.1. Отличие состоит лишь в том, что концентрации примесных ионов в растворе на несколько порядков ниже концентрации ионов целевого металла и поэтому J_м J_i. Поэтому можно принять, что суммарная плотность тока равна плотности тока восстановления ионов целевого металла:

J_м  J . (3.12)

С учетом этого допущения получается следующая зависимость содержания примеси от суммарной плотности тока:

A (3.13)

Плотности тока примеси и металла являются функциями концентрации ионов, температуры и потенциала (суммарной плотности тока), поэтому и А является функцией от этих же параметров. Поэтому, если известны уравнения парциальных кривых то, подстановкой их в выражение (3.13), можно получить количественные зависимость содержания примесей в металле от перечисленных параметров электролиза.

Отметим, что из-за низкой концентрации скорость восстановления ионов примесей в большинстве случаев контролируется диффузией или диффузией совместно с реакцией. Кинетический контроль наблюдается для компонентов, имеющих близкие величины равновесных потенциалов, а также при соосаждении примесей с металлами, имеющими высокие плотности тока обмена.

В отличие от восстановления примесных ионов, восстановление ионов целевого металла по целому ряду причин ведется в режимах, в максимальной степени предотвращающих диффузионные ограничения.

Поляризационные кривые при диффузионном контроле существенно разнятся от кривых при кинетическом контроле наличием точек перегиба и площадок предельного тока. По этому, как уже указывалось в разделе 3.2, различаются зависимости А- J и Вт- J.

Рассмотрим наиболее часто встречающиеся на практике случаи.

Cлучай 1. Ионы металла и примесей восстанавливаются с контролем скорости стадией разряда- ионизации.

Уравнения парциальных кривых полностью аналогичны таковым для совместного разряда металла и водорода:

ионы примесей -

ионы металла -

После подстановки уравнений кривых и замены активностей концентрациями получим уравнение зависимости содержания примеси и от потенциала

_,

из которого следует, что содержание примеси может по - разному зависeть от потенциала.

1. Не зависеть при b_i=b_m; 2. Возрастать при bibm;

3. Уменьшаться при b_i< b_m;

Так как и в этом случае для практики нужна зависимость содержания примеси не от потенциала, а от плотности тока, то ее можно получить следующим путем. Из уравнений для парциальных кривых можно получить обратные функции Е_i =F_i (c_i,T,J_i) и E_м = F_m(c_м, T, J_м). В рассматриваемом случае это уравнения Тафеля, отличающиеся величинами коэффициентов «а_Т» и «в_Т».

Учитывая, что при совместном разряде Е_м = Е_i , то, приравняв обратные функции, получим уравнение зависимости плотности тока примеси от плотности тока целевого металла. Подставляя его в выражение (3.13), получим искомую зависимость содержания примеси в металле как функцию концентрации ионов примеси и металла в растворе, плотности тока и констант скоростей восстановления ионов примесей и металла. Опуская алгебраические преобразования, приведем их конечный результат:

(3.14)

Входящие в это уравнение постоянные равны:

и

Коэффициент l=a_in_i/a_мn_м= (b)_м/(b)_i , то есть может быть определен по угловым коэффициентам парциальных поляризационных кривых, проведенных в координатах уравнения Тафеля.

Уравнение (3.14) получено создателями теории совместного разряда металла и примесей В.Л. Хейфецом и А.Л. Ротиняном в середине прошлого столетия и подтверждено на многочисленных примерах совместного разряда различных металлов. Из него следуют следующие выводы:

1). В зависимости от величины коэффициента  содержание примесей в металле может не зависеть от плотности тока (=1), возрастать с ее ростом (1) или уменьшаться (< 1).

2). Содержание примеси в металле пропорционально ее концентрации в растворе, коэффициент пропорциональности включает отношение констант скоростей реакции восстановления ионов, которое для разных сортов ионов может сильно различаться. По этой причине разные примеси будут включаться в катодный металл в разной степени при одинаковой концентрации в растворе.

3). Содержание примеси в металле уменьшается с увеличением концентрации ионов металла в растворе.

4). Как и в случае совместного разряда ионов металла и водорода, температура влияет на включение примесей через температурные зависимости констант скоростей реакций восстановления ионов металла и примеси. Если увеличение температуры увеличивает константу скорости восстановления примесей в большей степени, чем металла, то с ее увеличением осадок будет в большей степени загрязняться примесями и на оборот.

В качестве примеров, иллюстрирующих эти выводы, приведем некоторые экспериментальные данные[3] .

Рис. 3.9 иллюстрирует влияние природы примесей, a рис. 3.10- разный вид зависимостей от плотности тока.

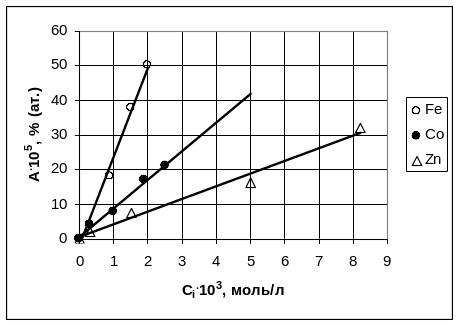
Рис.3.9. Включение примесей в катодное олово.

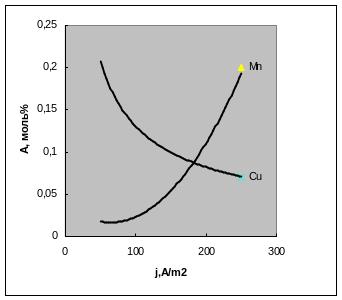
Рис.3.10. Включение меди и марганца в катодный осадок никеля

Случай 2. Ионы примесей восстанавливаются на предельном токе диффузии.

В этом случае уравнение для плотности тока восстановления ионов примесей записывается в виде:

, (3.15)

где D – коэффициент молекулярной диффузии ионов примеси;  - толщина диффузионного слоя. То есть, плотность тока восстановления примесей не зависит от потенциала и поэтому не зависит от плотности тока восстановления металла. Тогда, подставив уравнение (3.15) в выражение (3.12) и, объединив все постоянные в константу В, получим приближенное решение (рис. 3.11, кривая 1):

A= 1/(1 +J_м/J_i)  1/(1 +J/J_i) = BC_i/J (3.16)

Точное решение уравнения (3.16) отличается тем, что в некотором диапазоне плотностей тока до начала совместного разряда, когда на катоде восстанавливается одна примесь, А = 1. По достижении начала совместного разряда А будет уменьшаться в соответствии с кривой Вт-1 рисунка 1(п. 1.1). На рисунке 3.11 приведены приближенное и точное решения, которые довольно быстро сходятся.

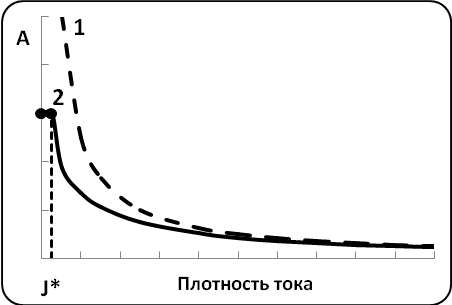
Рис. 3.11. Зависимость содержания примесей от плотности тока

Из уравнения (3.16) следует, что содержание примеси в катодном металле обратно пропорционально плотности тока и прямо пропорционально концентрации примеси в электролите. Так как коэффициенты диффузии различных ионов в растворах близки, то угловой коэффициент зависимости А от c одинаков для различных примесей. Рисунок 3.12 полученный на примере включения примесей в катодный никель, иллюстрирует это заключение.

Рис. 3.12. Зависимость содержания примесей в катодном никеле от их концентрации в электролите

Случай 3. Ионы примеси восстанавливаются с концентрационной поляризацией, ионы металла - с контролем скорости стадией разряда- ионизации.

Используя аналогичный способ анализа, нетрудно показать, что в этом случае содержание примесей в металле следующим образом зависит от плотности тока:

(3.17)

где k₁ = n_i /_мn_м и j ^* - плотность тока металла при равновесном потенциале примеси. Отличие этого случая состоит в том, что зависимость содержание примеси от плотности тока описывается кривой с максимумом. Вначале содержание примеси растет, достигает максимума и далее уменьшается (рисунок 3.13).

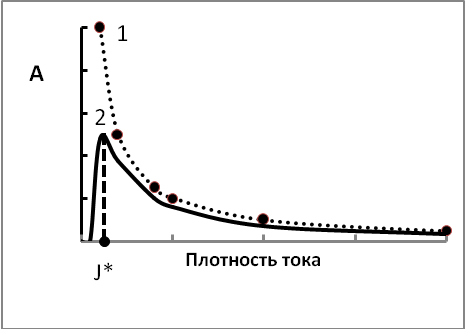
Рис. 3.13. Зависимость содержания примеси от плотности тока

Необходимо отметить, что зависимость содержания примеси от плотности тока в этом случае аналогична зависимости Вт₂ от плотности тока, полученной ранее (рис.3.5 п. 3.2).