2.4. Однополостный гиперболоид

П оверхность, определяемая уравнением (4), называется однополостным гиперболоидом.

Рассмотрим сечения однополостного гиперболоида

плоскостями:

1) плоскостью Oхy: – эллипс

2) плоскостью Oхz: – гипербола

3) плоскостью Oуz: – гипербола

4) плоскостью – эллипсы

2.5. Двуполостный гиперболоид

Поверхность, определяемая уравнением (5), называется двуполостным гиперболоидом.

Р ассмотрим сечения двуполостного гиперболоида плоскостями:

1) плоскостью Oхy:

– мнимые точки

не пересекается с плоскостью Oхy

2) плоскостью Oхz:

; – гипербола

3) плоскостью Oуz:

; – гипербола

4) плоскостью , – эллипсы

2.6. Эллиптический параболоид

Поверхность, определяемая уравнением , где , (6), называется эллиптическим параболоидом

Рассмотрим сечения эллиптического параболоида плоскостями:

1 ) плоскостью Oхy:

, – точка О(0,0,0)

не пересекается с плоскостью Oхy

2) плоскостью Oхz: – парабола

3) плоскостью Oуz: – парабола

4) плоскостью , – эллипсы

§ 3. Предел и непрерывность функции двух переменных

Определение: Окрестностью точки называется

внутренность круга с центром в точке . Если радиус круга ,

то имеем -окрестность т .

Определение: Число называется пределом функции двух

независимых переменных , если для любого сколь угодно малого положительного значения найдется такая -окрестность точки , что для любой точки из этой окрестности (за исключением, быть может, т. ) выполняется неравенство или , обозначается:

или

Определение: Функция называется непрерывной в т. , если она определена в т. и некоторой её окрестности, если существует предел функции в т. , равный значению функции в этой точке, т.е.

или

Определение: Функция называется непрерывной в области D, если она непрерывна в каждой точке этой области.

ТЕОРЕМА. Если функция непрерывна в ограниченной замкнутой области D, то она в этой области:

1. Ограничена, т.е. ;

2. Достигает своих наименьшего и наибольшего значений;

3. Принимает все промежуточные значения.

(Без доказательства)

§4. Частные производные функции двух переменных. Дифференцируемость функции двух переменных

Пусть в области D задана функция . Если считать постоянным, то функция будет функцией одной переменной x. Значит можно рассматривать её производную по . Если считать x постоянным, то будет функцией по переменной , и можно рассматривать производную по .

Возьмем т. , найдем . Дадим приращение , а оставим неизменным. Получим т. , найдем . Функция получит приращение – частное приращение функции по переменной x.

Аналогично, если получит приращение , а сохраняет постоянное значение, то функция получит приращение – частное приращение функции по переменной

Если получит приращение , а приращение , то функция получит приращение – полное приращение функции

Определение: Частной производной функции по называется предел отношения частного приращения по к приращению аргумента при

Обозначается: ; ;

Определение: Частной производной функции по называется предел отношения частного приращения по к приращению аргумента при

вычисляется в предположении, что

вычисляется в предположении, что

Частные производные вычисляются по тем же правилам и формулам, что и производные функции одной переменной.

Примеры:

1. ;

2. ;

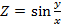
3. Доказать, что удовлетворяет уравнению

Решение:

;

Определение: Функция называется дифференцируемой в т. , если её полное приращение в этой точке можно представить в виде

(1)

где и – постоянные (не зависят от а зависят от координат т. )

при

(1) можно записать в виде , где – расстояние от т. до т. . Слагаемое , линейное относительно и , называют главной частью приращения функции.

ТЕОРЕМА 1. Если функция дифференцируема в т. , то она непрерывна в этой точке.

ТЕОРЕМА 2. (необходимое условие дифференцируемости функции) Если функция дифференцируема в т. , то она имеет в этой точке частные производные , , причем (2)

ТЕОРЕМА 3. (достаточное условие дифференцируемости функции) Если функция имеет частные производные в некоторой окрестности т. , непрерывные в самой этой точке, то она дифференцируема в этой точке.

Замечание. Для функции одной переменной понятия «дифференцируемости» и «существования производной» равносильны. Для функции нескольких переменных (в частности двух) утверждения «функция дифференцируема в данной точке» не равнозначно утверждению «функция имеет частные производные по всем переменным в этой точке».