Приложение 3: Описание функции впр

Функция ВПР имеет 3 аргумента и записывается в виде:

ВПР(<искомое значение>;<справочная таблица>;<номер столбца справочной таблицы> [;<режим просмотра>])

Первый аргумент <искомое значение> содержит значение, которое ищется в первом столбце справочной таблицы. Это значение может быть константой любого типа или ссылкой. Константы текстового типа или типа дата, время, дата-время должны заключаться в кавычки.

Второй аргумент <справочная таблица> содержит описание местоположения справочной таблицы. Первая строка этой таблицы не должна содержать обозначения столбцов.

Третьим аргументом <номер столбца справочной таблицы> задается номер столбца, из которого берется значение функции ВПР.

Вычисление функции ВПР сводится к поиску значения первого аргумента в первом столбце справочной таблицы (стрелка, направленная сверху вниз на рис. 25). В строке, в которой находится найденное значение, выбирается клетка, принадлежащая столбцу, указанному третьим аргументом (стрелка, направленная слева направо до столбца зеленого цвета). Значение этой клетки присваивается значению функции ВПР (красная стрелка).

Рис. 25. Пояснительная схема вычисления функции ВПР.

Четвертый необязательный аргумент функции ВПР <режим просмотра> определяет поведение Excel при поиске значения первого аргумента в первом столбце справочной таблицы. Он может принимать одно из логических значений - ИСТИНА или ЛОЖЬ.

Если <режим просмотра> = ИСТИНА или отсутствует, справочная таблица должна быть упорядочена по закону роста значений первого столбца, т.е. столбца, в котором Excel ищет значение первого аргумента.

В этом случае Excel не обязательно находит точное значение первого аргумента в первом столбце справочной таблицы. Если в столбце нет значения, равного искомому, берется ближайшее значение меньшее искомого. Если такового нет - выводится сообщение об ошибке #Н/Д.

Лабораторная работа 2. Исследование методов дискретизации непрерывных сообщений по времени

Цель работы -: Закрепление теоретических знаний и приобретение практических навыков применения методов дискретизации непрерывных сигналов по времени.

Теоретическое введение.

Теория дискретизации непрерывных сигналов по времени изложена в главе 2 учебного пособия по дисциплине Теория информации и кодирование [1].

В данной лабораторной работе предлагается экспериментально подтвердить:

1) высокую экономичность представления и точность восстановления исходного сигнала с помощью ряда Котельникова;

2) соответствие максимального значения ошибки восстановления расчетному при использовании для восстановления полиномов Лагранжа разных степеней.

В качестве квантуемого непрерывного сигнала берется звук вашего голоса, пропущенный через фильтр, ограничивающий спектр сигнала сверху. Современные операционные системы, в частности Windows, имеют в своем составе средства записи и воспроизведения звука. Необходимо только, чтобы компьютер был оснащен звуковой картой. Индивидуальность голоса обеспечивает различие получаемых результатов.

Для решения первой задачи используется теорема Найквиста-Котельникова, согласно которой для абсолютно точного восстановления непрерывного сигнала по отсчетам, взятым с постоянным шагом , нужно, чтобы этот шаг был взят в соответствии с неравенством: , где f_m – частота, выше которой спектр квантуемого сигнала равен 0.

Если шаг дискретизации отвечает этому условию, то согласно теореме Найквиста-Котельникова исходный сигнал x(t) можно восстановить при всех значениях времени (аргумента t) по формуле (ряд Котельникова):

(1)

Здесь:

x(t) – исходная дискретизируемая функция;

- отсчеты функции x(t), взятые в моменты времени

- круговая частота.

Проблема, однако, заключается в том, что, как доказано математически, поскольку все реальные сигналы конечны во времени, их спектры не ограничены по частоте. Следовательно, на самом деле для всех реальных сигналов 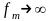. Поэтому в чистом виде теорему Найквиста-Котельникова применить невозможно. Тем не менее, ее используют, пренебрегая малыми значениями спектра. Это и предлагается сделать в этой работе. Платой за такое пренебрежение будет неточное выполнение равенства (1).

Решение второй задачи основано на использовании формулы максимального значения ошибки (отклонения восстановленного значения функции от исходного):

(2)

Здесь - абсолютное значение ошибки;

n – порядок полиномов Лагранжа, используемых для восстановления исходной функции;

- максимальное значение абсолютной величины производной (n+1)–го порядка исходного сигнала x(t);

t – текущее время;

t_i – время взятия i-го отсчета.

Используя эту формулу, задавшись максимально допустимым значением ошибки восстановления исходной функции по периодически взятыми отсчетам, и порядком используемых в воспроизводящей функции полиномов Лагранжа, можно найти максимально возможный шаг квантования (чем шаг квантования больше, тем лучше, поскольку тем меньше приходится брать отсчетов).

В следующей ниже таблице приведены формулы расчета максимального шага дискретизации по времени в зависимости от порядка n полинома Лагранжа и максимально допустимого значения ошибки

n – порядок используемых для восстановления исходного процесса полиномов Лагранжа
0
1

Эти формулы и предлагается использовать в данной работе. Их вывод приводится в методическом пособии [1].