3.8.2. Простейшие модели цифровых каналов связи с помехами

Свойство помехоустойчивых кодов обнаруживать и исправлять ошибки в сильной степени зависит от характеристик помех и канала передачи информации. В теории информации обычно рассматривают две простые модели дискретного (цифрового) канала. Ими являются:

1. двоичный симметричный канал (ДСМК);

2. двоичный стирающий канал (ДСТК).

При передаче информации через ДСМК помеха способна с некоторой вероятностью Р превратить 0 в 1 или 1 в 0. Передачу информации через ДСМК можно представить в виде следующего графа, изображенного на рис. 3.5:

Рис. 3.5. Двоичный симметричный канал.

Двоичный стирающий канал также описывается вероятностью Р искажения передаваемого символа, однако в результате искажения передаваемый символ стирается, что отражается следующим графом, изображенном на рис. 3.6:

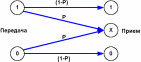
Рис. 3.6. Двоичный стирающий канал.

Здесь Х – нейтральный символ.

В дальнейшем воспользуемся моделью ДСМК. Его преимущество заключается в исключительной простоте.

3.8.3. Расчет вероятности искажения кодового слова в дсмк

Положим, кодовое слово состоит из n двоичных символов. Вероятность неискажения кодового слова, как несложно доказать, равна:

.

Вероятность искажения одного символа (однократная ошибка):

и любого ко символов (ко – кратность ошибки):

.

Нетрудно заметить, что если Р < 0,5 , то с ростом кратности ошибки ко ее вероятность Р_ко уменьшается. Это следует из того, что P_ко всегда представляет собой произведение n сомножителей, ко из которых P < 0,5 а n-ко (1-P)>0,5. С увеличением кратности ошибки ко число больших сомножителей (1-Р) уменьшается, а меньших Р – увеличивается. Это приводит к тому, что произведение Р_ко , т.е. вероятность ошибки, с ростом ее кратности в целом уменьшается.

Таким образом, в ДСМК наиболее вероятны ошибки с меньшей кратностью. Следовательно, такие ошибки следует исправлять в первую очередь.

3.8.4. Общие принципы использования избыточности

Для простоты рассмотрим блоковый код. С его помощью каждым k разрядам (буквам) входной последовательности ставится в соответствие n-разрядное кодовое слова. Количество разного вида k-разрядных информационных комбинаций равно 2^k. Каждой из них ставится в соответствие определенное кодовое слово. Их также 2^k. Эти кодовые слова называются разрешенными.

Однако возможное число n-разрядных комбинаций равно 2ⁿ. Если из этого числа исключить все разрешенные кодовые слова, то останутся запрещенные кодовые слова.

Кодер посылает в линию связи только разрешенные кодовые слова, однако под действием помех они могут превратиться в любое другое из 2ⁿ возможных − в другое разрешенное или в запрещенное. Все запрещенные слова данного кода заранее известны. Поэтому факт получения такого кодового слова легко устанавливается и является верным признаком наличия в кодовом слове ошибки – ошибка обнаруживается.

Возможность исправления ошибки связана со свойством кода, называемого кодовым расстоянием.

Определить кодовое расстояние невозможно без предварительного определения другого понятия – расстояние между кодовыми словами.

Под расстоянием между кодовыми словами понимают количество различий в одноименных разрядах двух кодовых слов.

Если, например, одно кодовое слово имеет вид 011101001, а другое – 111001100, то расстояние между ними можно вычислить, выполнив операцию XOR (исключенное или) и подсчитав количество единичных разрядов в результате:

0 1 1 1 0 1 0 0 1

XOR

1 1 1 0 0 1 1 0 0

_______________________________________________

1 0 0 1 0 0 1 0 1

Расстояние между кодовыми словами, как видим, равно 4. Ниже будем расстояние между кодовыми словами обозначать буквой d. В данном примере d=4.

Вспомним, что весом кодового слова двоичного кода называют число единичных разрядов в нем. Тогда кодовое расстояние равно весу поразрядной суммы по модулю 2 кодовых слов, расстояние между которыми определяется.

Выше мы показали, что наиболее вероятными в случае ДСМК являются однократные ошибки, и, чем выше кратность ошибки, тем менее она вероятна. Возникновение ко-кратной ошибки можно трактовать как преобразование передаваемого кодового слова в другое, находящееся на расстоянии ко от передаваемого. Ясно, что переводы на меньшие расстояния более вероятны.

Геометрически множество разрешенных кодовых слов условно можно отобразить в виде точечного множества (рис. 3.7).

Рис. 3.7. Точечное множество.

Теперь можно определить понятие кодового расстояния.

Кодовым расстоянием данного кода называют наименьшее расстояние между разрешенными кодовыми словами этого кода. Ниже оно обозначается d_min.

В литературе по кодированию кодовое расстояние еще называют Хэминговым – по фамилии ученого, впервые его предложившего.

Продолжим изучение общих принципов использования избыточности.

Напомним, что вероятность определенной 2-кратной ошибки определяется формулой: . Но таких ошибок может быть несколько. Если, к примеру, кодовое слово состоит из 5 символов, то возможны ошибки в 1 и 5, 1 и 4, 1 и 3, 1 и 2, 2 и 5, 2 и 4, 2 и 3, 3 и 5, 3 и 4, 4 и 5 разрядах. Итого 10 различных 2-кратных ошибок. Их число равно числу сочетаний из 5 элементов по 2.

Если говорить не о конкретных, а о произвольных ко-кратных ошибках, то вероятность их возникновения находится как сумма всех возможных i-кратных конкретных ошибок:

,

где − число сочетаний из n элементов по ко.

Следует заметить, что в отличие от Р_ко не обязательно монотонно уменьшается с ростом n.

При получении искаженного кодового слова мы имеем дело с конкретной ко-кратной ошибкой, вероятность появления которой − Р_ко . Эта вероятность монотонно уменьшается с ростом кратности ошибки ко. Поэтому при обнаружении на выходе канала запрещенного кодового слова наиболее вероятным является то, что было передано разрешенное кодовое слово, отличающееся от полученного в наименьшем числе разрядов, т.е. находящееся от него на ближайшем расстоянии.

Если код имеет кодовое расстояние d_min , то гарантией обнаружения ошибки будет ко<d_min. В этом случае помехи не смогут преобразовать одно разрешенное кодовое слово в другое разрешенное, поскольку расстояние до ближайшего разрешенного слова равно d_min.

Если кратность ошибки превысит кодовое расстояние, она также может быть обнаружена, но не всегда.

Гарантией же правильного исправления ошибки будет условие ко<d_min/2, так как согласно свойству вероятности ошибки наиболее вероятны ошибки с меньшей кратностью и, следовательно, исправление будет производиться в сторону ближайшего разрешенного кодового слова (рис. 3.8).

Рис. 3.8. Кодовое расстояние.

Для того, чтобы это исправление было верным, необходимо выполнение условия ко<d_min/2.

В связи с этим введено понятие корректирующей способности кода.

Под корректирующей способностью кода понимается максимальная кратность исправляемой с применением этого кода ошибки.

Учитывая вышеприведенные рассуждения, корректирующую способность кода KCK можно было бы определить по формуле:

.

На практике же, учитывая увеличение вероятности ошибочного исправления ошибки с ростом ее кратности, реальную корректирующую способность уменьшают:

.

В наших рассуждениях мы предполагали использование ДСМК. Если же реальный канал этой модели не соответствует, способы обнаружения и коррекции ошибок видоизменяются.

В общем же процедура обнаружения-исправления ошибок опирается на разбиение всего множества 2ⁿ возможных кодовых комбинаций на 2^k подмножеств, каждое из которых состоит из одного разрешенного кодового слова и соответствующих ему запрещенных. Эти подмножества не пересекаются между собой, а их объединение не обязательно равно исходному множеству.

При приеме определяется, к какому подмножеству относится принятое кодовое слово и, если оно (кодовое слово) не является разрешенным, оно заменяется закрепленным за этим подмножеством разрешенным кодовым словом.

Если же принятое кодовое слово не принадлежит ни одному из подмножеств, фиксируется неисправимое искажение, за чем могут следовать какие-либо дополнительные меры, например, запрос на повторную передачу искаженной части сообщения.