2.5.2. Дисперсия ошибки в случае использования равномерной шкалы квантования по уровню

Найдем дисперсию ошибки в случае использования равномерной шкалы квантования, т.е. равенства всех шагов квантования.

В этом случае:

и

Следовательно при постоянном шаге квантования дисперсия ошибки квантования находится по формуле (2.21)

2.5.3. Расчет неравномерной оптимальной в смысле минимума дисперсии ошибки шкалы квантования.

З

Рис. 2.19. Обозначения

ададимся теперь числом шагов квантования n, границами интервала (x_min, x_max) значений квантуемой величины, покрываемой шагами квантования (рис. 2.19), и найдем такое распределение шагов на интервале, которое минимизирует дисперсию ошибки или, что то же самое, среднее значение ее квадрата.

Введем вспомогательную переменную .

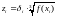Тогда, учитывая (2.19), дисперсия ошибки квантования: (2.22)

Заметим, что

(2.23)

Рис. 2.20. Вариант системы с использованием неравномерного квантования.

− функционал от плотности распределения вероятностей – некоторое число.

Теперь найдем такой набор z_i, при котором дисперсия ошибки минимальна. Для этого воспользуемся методом множителей Лагранжа.

Таким образом, минимизируется функция (2.22) при условии (2.23).

Вспомогательная функция Ф в этом случае принимает вид:

.

В результате получаем систему уравнений: .

Из верхнего уравнения следует, что , т.е. все z_i равны. Учитывая это, из нижнего уравнения получаем .

После подстановки z_i в (2.22) получаем следующую формулу:

(2.24)

Эту формулу и используют для построения оптимальной шкалы квантования по уровню. Но прежде, чем приступить к ее построению, рассмотрим одну из технических систем, в которой эта шкала применяется на практике.

На рис. 2.20 изображена блок-схема варианта системы с использованием неравномерного квантования по уровню.

С помощью компрессора выполняется нелинейное преобразование входного сигнала x(t) в выходной y(t). Преобразование описывается формулой:

.

При помощи экспандера выполняется обратное преобразование: .

Здесь - функция, обратная функции .

Связь между сигналами x и y и наоборот называется законом компандирования (от первых слогов слова компрессор и последних слогов слова экспандер).

Таким образом, закон компандирования связывает равномерную и неравномерную, в данном случае оптимальную, шкалы квантования по уровню.

Э

Рис. 2.21. График варианта закона компандирования.

то позволяет в технических решениях пользоваться стандартными равномерными аналого-цифровыми (АЦП) и цифроаналоговыми (ЦАП) преобразователями.

График возможного варианта закона компандирования изображен на рис. 2.21.

Найдем его формулу для случай оптимального квантования при следующих условиях:

y_min = x_min

y_max = x_max

Последнее условие отражает способность функции y(x) преобразовывать оптимальную неравномерную шкалу квантования сигнала x(t) в равномерную шкалу квантования сигнала y(t).

При больших n можно считать, что:

и

тогда (2.25)

Учитывая, что и ,

получим . Подставив последнее выражение в (2.25), получим: ;

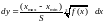- дифференциальное уравнение первого порядка с разделяющимися переменными.

Интегрируя левую его часть от y_min до y, а правую часть от x_min до x, получим:

Отсюда получаем закон компандирования:

(2.26)

Таким образом, закон компандирования описывается функцией . К сожалению, пока не найдена простая обратная функция . Но именно эта обратная функция нам более всего и нужна, т.к. процедура построения оптимальной шкалы квантования предусматривает разбиение интервала [y_min , y_max] на n равных шагов и определение с границ интервалов неравномерной шкалы при помощи функции .

Поэтому процедура поиска границ шагов квантования неравномерной оптимальной шкалы квантования сейчас предусматривает использование компьютера для вычисления интеграла, входящего в правую часть формулы (2.26). Вычисление интеграла, как это обычно делается, заменяется вычислением суммы. По мере накопления слагаемых верхняя граница определенного интеграла растет. По мере пересечения значений y_i находятся соответствующие им значения x_i. В результате к концу интегрирования находятся все границы интервалов квантования неравномерной шкалы.

В заключение отметим, что в ряде случаев оптимальное квантование позволяет в десятки раз снизить дисперсию ошибки квантования или уменьшить число передаваемых отсчетов по сравнению со случаем применения равномерного квантования.