2.4.2.4. Расчет периода дискретизации при использовании для получения воспроизводящей функции полинома Лагранжа нулевого порядка
Интерполяция полиномами нулевого порядка n=0.
Таких полиномов всего 1:
,
отсюда
при
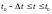
Воспроизводящая функция при использовании полиномов Лагранжа нулевого порядка имеет вид ступенчатой кривой (рис. 2.10).
Рис. 2.10. Воспроизводящая функция при использовании для восстановления полиномов Лагранжа нулевого порядка.
Подставив n=0 в формулу максимальной погрешности, по заданной погрешности найдем максимальный шаг квантования:
,
отсюда
и
.
2.4.2.5. Расчет периода дискретизации при использовании для получения воспроизводящей функции полинома Лагранжа первого порядка
Интерполяция полиномами первого порядка n=1.
Таких полиномов оказывается всего 2:
;
.
Видно, что последнее уравнение – уравнение прямой.
В графической форме такая интерполяция выглядит в виде ломаной линии (рис. 2.11).
Рис. 2.11. Воспроизводящая функция при использовании для восстановления полиномов Лагранжа первого порядка.
Найдем .
Для этого приравняем производную этой величины по t к нулю:
=0.
Отсюда .
Вторая производная отрицательна. Это означает, что найден именно максимум.
Теперь подставим найденное t в формулу максимальной погрешности:
;
и
найдем шаг дискретизации:
.
2.4.2.6. Расчет периода дискретизации при использовании для получения воспроизводящей функции полинома Лагранжа второго порядка
Интерполяция полиномами второго порядка n=3
− парабола.
2.4.2.7. Обобщение на случай использования полиномов Лагранжа произвольного порядка
Интерполяция полиномами n-го порядка рассматривается аналогично предыдущим случаям. При этом наблюдается значительное усложнение формул. Обобщение приводит к формуле следующего вида:
−
некоторая
функция n.
Кроме того, для Mn+1 выведена оценка сверху:
Таблица 2.1.
n |
|
1 |
89,5 |
2 |
250 |
3 |
395 |
4 |
504 |
, где |x(t)|max – макcимальное значение x(t) на отрезке интерполяции.
При
увеличении порядка полинома максимально
допустимое значение
быстро растет. Это при
показано в таблице 2.1.
В ней показано во сколько раз возрастает максимально возможный период дискретизации при получении воспроизводящей функции полинома n-го порядка по сравнению со случаем использования для этих же целей полинома нулевого порядка при максимальной ошибке, равной 0,1% от Xmax.
2.4.3. Выбор интервала дискретизации по критерию среднеквадратического отклонения
Рассмотрим
случай дискретизации случайного
стационарного эргодического процесса
x(t)
с известной
корреляционной функцией
.
Восстанавливать будем при помощи
полиномов Лагранжа. Наиболее часто
используются полиномы нулевого и первого
порядка.
Начнем с полинома нулевого порядка.
Ошибка,
как известно, вычисляется по формуле:
Дисперсия
ошибки
в случае стационарных эргодических
процессов может быть вычислена по
формуле:
,
где
−
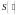оператор усреднения по времени,
−
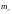среднее значение (математическое
ожидание) ошибки.
Найдем
:
,
−
оператор
математического ожидания.
Значит
.
Найдем каждое из этих средних.
1)
;
2
)
по аналогичной причине;
3) .
В итоге:
Отсюда
Используя эту формулу, шаг дискретизации можно найти графически так, как показано на рис. 2.12.
Рис. 2.12. Порядок графического определения шага дискретизации, если использовать критерий среднеквадратического отклонения.
В заключение отметим, что найдены также выражения для дисперсии ошибки и при восстановлении с помощью полиномов более высоких, чем нулевой, порядков.